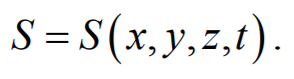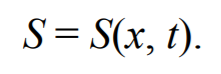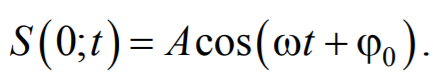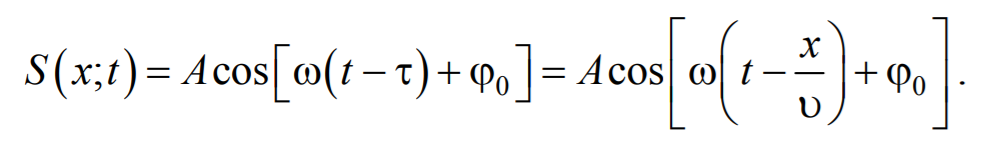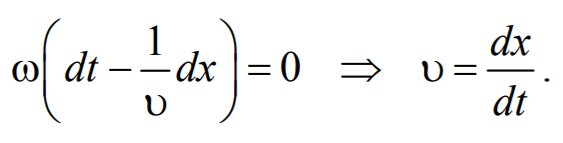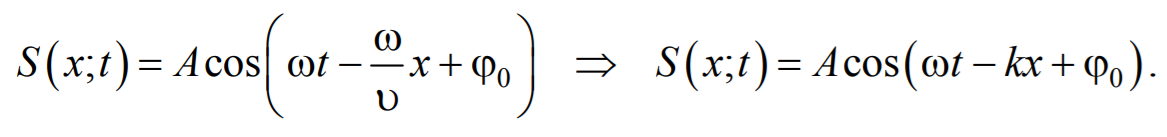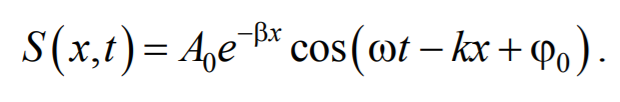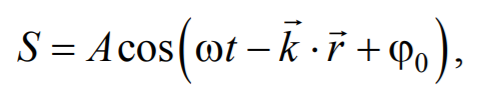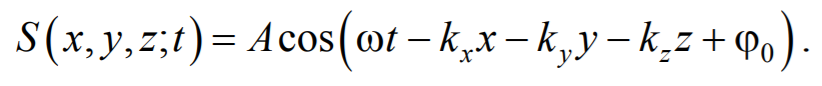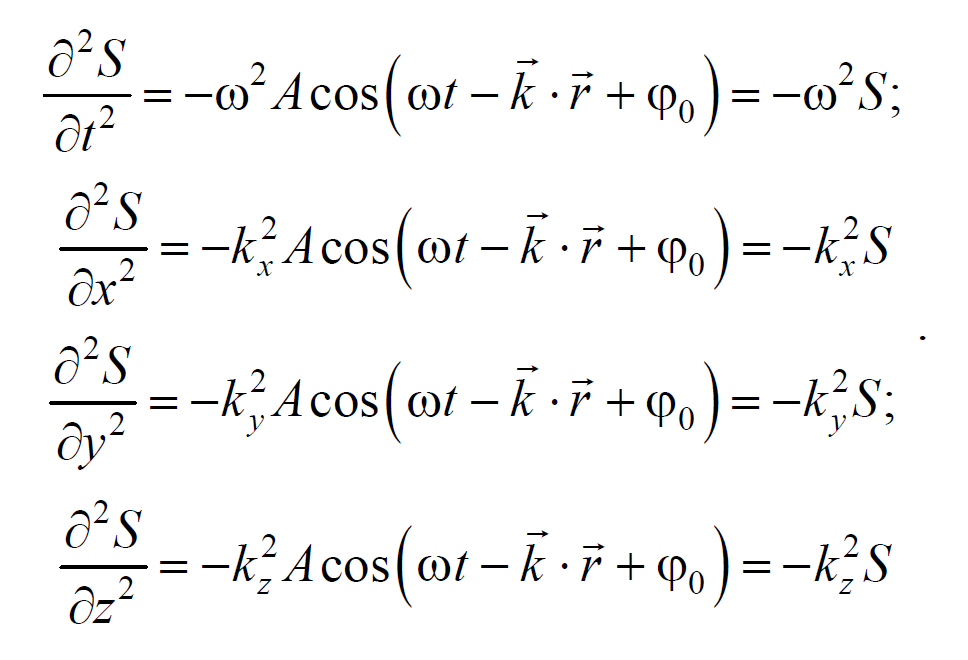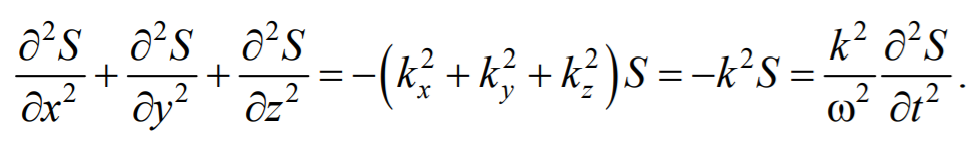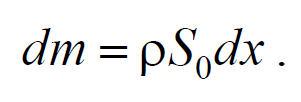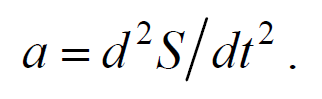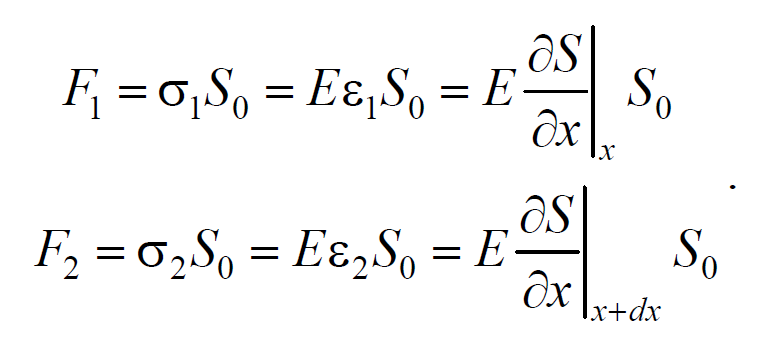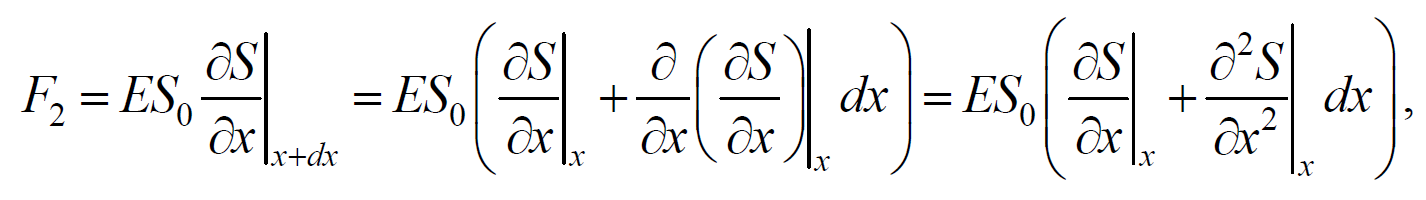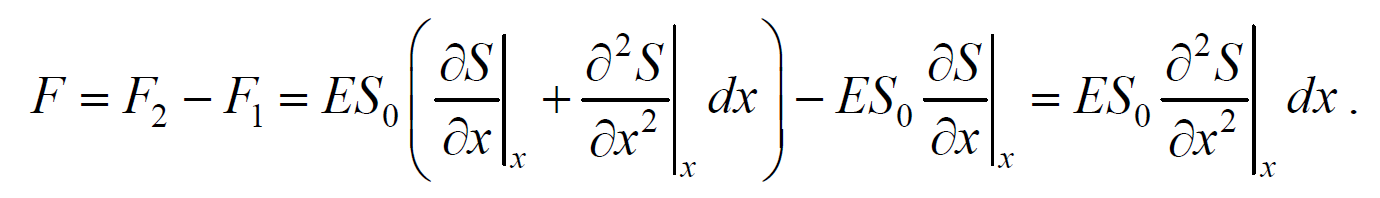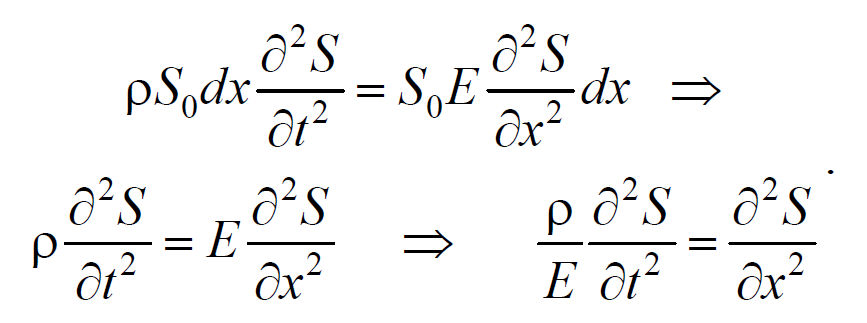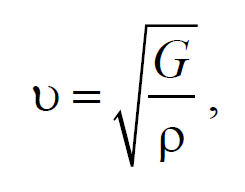какие волны возникают в результате упругих деформаций

Упругие волны (механические волны).

Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.

Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.

Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.

Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.

Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д. Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.

Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.

В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.

Продольная волна.

Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.

В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).

Пример распространения продольной упругой волны изображен на рисунке а и б выше. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближа­ются, возникает сила упругости, под действием которой эти витки начинают расходиться. Про­должая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение (рисунок б). При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положе­ния равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.

Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными. В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других.

Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.

Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.

В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде воли в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одина­ковыми фазами.

Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называ­ется волновой поверхностью, или фронтом волны.

С этой точки зрения плоской волне можно дать и следующее определение:

Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.

Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.

Уравнение плоской синусоидальной волны имеет вид:

где s — смещение колеблющейся точки, s_m — амплитуда колебаний, ω — циклическая частота, t — время, х — текущая координата, v — скорость распространения колебаний или скорость волны, φ₀ — начальная фаза колебаний.

Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.

Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.

Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:

.

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Упругие волны

Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.

Содержание

Классификация

В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.

В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.

В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.

Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.

Упругие волны в твёрдых телах

Наиболее распространёнными типами упругих волн в твёрдых телах являются:

Практическое применение

Упругие волны широко используются:

См. также

УПРУГИЕ ВОЛНЫ — (см. (4)), распространяющиеся в среде, которая обладает (см.). Они возникают при колебаниях твёрдых тел, взрывах, землетрясениях и т. п. Скорость их распространения зависит от величины (см.) … Большая политехническая энциклопедия

УПРУГИЕ ВОЛНЫ — УПРУГИЕ ВОЛНЫ, механические возмущения, распространяющиеся в упругой (твердой, жидкой или газообразной) среде. Возникают при колебаниях твердых тел, взрывах, землетрясениях; звук также является упругой волной … Современная энциклопедия

УПРУГИЕ ВОЛНЫ — механические возмущения, распространяющиеся в упругой (твердой, жидкой или газообразной) среде. Возникают при колебаниях твердых тел, взрывах, землетрясениях; звук также является упругой волной … Большой Энциклопедический словарь

Упругие волны — – механические возмущения, распространяющиеся в упругой (твердой, жидкой или газообразной) среде; возникают при колебаниях твердых тел, взрывах, землетрясениях. [Терминологический словарь по бетону и железобетону. ФГУП «НИЦ «Строительство»… … Энциклопедия терминов, определений и пояснений строительных материалов

упругие волны — механические возмущения, распространяющиеся в упругой (твёрдой, жидкой или газообразной) среде. Возникают при колебаниях твердых тел, взрывах, землетрясениях; звук также является упругой волной. * * * УПРУГИЕ ВОЛНЫ УПРУГИЕ ВОЛНЫ, механические… … Энциклопедический словарь

Упругие волны — упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Например, Волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит… … Большая советская энциклопедия

УПРУГИЕ ВОЛНЫ — механич. возмущения (деформации), распространяющиеся в среде, к рая обладает упругостью. Жидкости и газы обладают объёмной упругостью и не обладают упругостью формы. В них могут образовываться только продольные волны разрежения сжатия, в к рых… … Большой энциклопедический политехнический словарь

УПРУГИЕ ВОЛНЫ — механич. возмущения (деформации), распространяющиеся в тв., жидкой или газообразной среде. В жидкостях и газах, не обладающих упругостью формы, могут образовываться только продольные волны разрежения сжатия, в к рых частицы среды колеблются вдоль … Естествознание. Энциклопедический словарь

Источник

Упругие волны

Упругие волны — процесс распространения в упругой среде механических деформаций. Различают два вида упругих волн — продольные и поперечные.

Продольными называются волны, в которых колебания частиц среды происходят в направлении распространения волны. Упругие продольные волны связаны с объемной деформацией упругой среды и поэтому могут возникать в любых средах — твердых, жидких и газообразных.

Поперечными называются такие волны, в которых колебания частиц среды происходят в направлении, перпендикулярном к направлению распространения волны. Упругие поперечные волны могут распространяться лишь в средах, обладающих упругой деформацией сдвига, т.е. в твердых телах. Исключением из этого являются высокочастотные (n

10 10 Гц) гиперзвуковые волны, возбуждаемые в жидкостях, которые (см. § 10.2) при таких частотах ведут себя как твердые тела, и поверхностные волны, возникающие на границе раздела двух жидких или жидкой и газообразной фаз.

Найдем уравнение гармонической одномерной упругой волны называемой часто бегущей волной.

Пусть источник волн S колеблется в упругой среде по гармоническому закону

Рис. 22.1

,

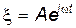
где x – смещение от положения равновесия в момент времени t.

Колебания в точке M, отстоящей от источника на расстояние x (рис. 22.1), совершаются по закону .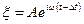

где 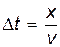— время, в течение которого волновой фронт достигает точки M.

Таким образом, .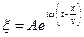

(22.1)

Это и есть уравнение бегущей волны. Здесь x — смещение от положения равновесия в точке пространства с координатой x в момент времени t.

Длиной волны называется расстояние между двумя ближайшими точками, колеблющейся в одинаковой фазе. Длина волны численно равна пути, который проходит передний фронт волны за время, равное периоду колебаний

.

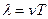
Преобразуем выражение для фазы волны следующим образом:

.

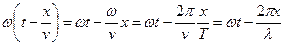
Тогда уравнение волны можно представить в виде

.

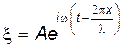(22.2)

Уравнения (22.1) и (22.2) эквивалентны.

Продифференцируем уравнение (22.1) дважды по координате x и по времени t:

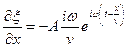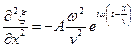; ;	(22.3)
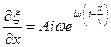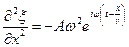; ;	(22.4)

Из (22.3) и (22.4) следует

.

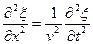(22.5)

Дифференциальное уравнение (22.5) называется волновым уравнением. Решением этого уравнения может быть любая волна с произвольной формой фронта.

Источник

Лекция №9. Механические волны

6.1. Распространение колебаний в упругой среде

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.

6.2. Уравнение плоской волны

Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t

где А − амплитуда волны; ϕ₀ − начальная фаза волны (определяется выбором начал отсчета х и t ).

Тогда уравнение плоской волны будет иметь вид

6.3. Волновое уравнение

Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид

где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности

Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.

Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)

Сложив производные по координатам, и с учетом производной по времени, получим

6.4. Скорость распространения волн в различных средах

где Е − модуль Юнга среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

где ρ − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

После разложения силы F₂ в ряд, получим

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

Источник