Каким параметром характеризуют интенсивность броуновского движения

Броуновское движение

Броуновское движение (или брауновское движение) – это непрерывное хаотическое движение малых частиц, взвешенных в жидкости или газе (при этом подразумевается, что сила тяжести не влияет на их движение).

Это явление впервые наблюдал Роберт Броун (Браун, годы жизни 1773 – 1858), когда рассматривал в микроскоп движение цветочной пыльцы, взвешенной в воде. В наше время для таких наблюдений используют маленькие части краски гуммигут, которая не растворяется в воде. В газе броуновское движение совершают, например, взвешенные в воздухе частицы пыли или дыма.

Броуновское движение частицы возникает потому, что импульсы, с которыми молекулы жидкости или газа действуют на эту частицу, не компенсируют друг друга. Молекулы среды (то есть молекулы газа или жидкости) движутся хаотично, поэтому их удары приводят броуновскую частицу в беспорядочное движение: броуновская частица быстро меняет свою скорость по направлению и по величине.

Броуновское движение – это тепловое движение, интенсивность которого возрастает с ростом температуры среды и продолжается неограниченно долго без каких-либо видимых изменений. Интенсивность броуновского движения также возрастает с уменьшением размера и массы частиц, а также при уменьшении вязкости среды.

Броуновское движение служит наиболее наглядным экспериментальным подтверждением существования атомов (молекул) и их хаотического теплового движения. Полная молекулярно-кинетическая теория броуновского движения была дана в 1905 – 1906 годах немецким учёным Альбертом Эйнштейном (1879 – 1955) и польским физиком Марианом Смолуховским (1872 – 1917). В 1908 – 1911 годах французский учёный Жан Перрен (1870 – 1942) провёл серию экспериментов по изучению броуновского движения и окончательно подтвердил закономерности этого движения, предсказанные на основе молекулярно-кинетической теории.

Рис. 1.2. Траектория движения броуновской частицы (частиц краски гуммигута в воде по Перрену).

Броуновское движение, например, в метрологии, является основной причиной, по которой точность чувствительных измерительных приборов ограничена, потому что тепловое движение атомов деталей приборов и окружающей среды вызывает дрожание стрелок измерительных приборов.

Источник

Броуновское движение

Важнейшим фактором, влияющим на молекулярно-кинетические свойства золей, является броуновское движение частиц дисперсной фазы. Оно названо в честь английского ботаника Роберта Броуна, который впервые наблюдал его в 1827 г., исследуя под световым микроскопом взвесь цветочной пыльцы в воде. Ученый обнаружил, что частицы пыльцы непрерывно двигаются по сложным траекториям, ни на мгновение не оставаясь в покое. Причину данного движения долгое время установить не могли и считали его проявлением особенностей исключительно живой материи. Однако такое объяснение вскоре было отвергнуто, т.к. обнаружили, что подобное непрерывное движение могут совершать и неорганические частицы, взвешенные в жидкости или газе.

Таким образом, была установлена универсальность броуновского движения.

Дальнейшие исследования показали, что отдельные частицы двигаются совершенно независимо одна от другой. Их перемещение происходит тем интенсивнее, чем меньше размеры частиц и вязкость среды и совершенно не зависят от природы измельченного вещества.

В свободно-дисперсных системах с газовой или жидкой дисперсионной средой коллоидные частицы также не зафиксированы в каких-то определенных позициях. Они участвуют в броуновском движении, которое является прямым следствием теплового движения молекул растворителя и их беспорядочных ударов о данную частицу. Причем чем меньше размеры частицы, тем меньшее число молекул ударяется о ее поверхность. Это, в свою очередь, приводит к тому, что различия по числу и силе ударов с каждой стороны частицы становятся более значительными. Частица в любой момент времени движется в ту сторону, с которой результирующая величина ударов меньше. Само ее движение является скачкообразным и хаотическим. Скачки совершаются с большой частотой и в произвольном направлении, то есть независимо от того, каким был предшествующий скачок. Кроме того, скачки имеют разную длину. Установлено, что коллоидная частица изменяет направление своего движения приблизительно 10 12 раз за 1 секунду. Проследить действительный путь частицы при

Мариан Смолуховский (1872 – 1917), польский физик-теоретик. Окончил университет в Вене (1894), в 1896-1897 работал в университетах Парижа, Глазго и Берлина. С 1900 профессор Львовского университета (позднее ректор), с 1913 профессор Краковского университета. Основные труды по статистической физике. Работы Смолуховского по теории флуктуаций (1904) и броуновского движения (1906) наряду с работами Альберта Эйнштейна являются основополагающими в этой области. Смолуховский создал на основе теории броуновского движения кинетическую теорию коагуляции коллоидов, теорию электрокинетических явлений, заложив фундамент кинетической теории коллоидных систем.

таком движении не представляется возможным. Поэтому за меру, характеризующую интенсивность броуновского движения, принимают так называемое смещение частицы или ее сдвиг (∆Х). Это проекция расстояния между двумя положениями частицы (А и В) за время t, разделяющее два смежных наблюдения (рис. 56).

Рис. 56. Схема броуновского движения частицы

Смещения частицы за одинаковые промежутки времени t обычно не совпадают как по величине, так и по направлению, поэтому на практике используют так называемый среднеквадратичный сдвиг частицы :

где ∆Х₁, ∆Х₂, ∆Х₃, … – отдельные проекции смещения частицы за одно и тоже время t;n – число определяемых проекций смещения частицы за определенное время t.

Точную количественную оценку броуновского движения частицы можно дать с помощью уравнения Смолуховского-Эйнштейна:

η – вязкость дисперсионной среды;

r – радиус частицы дисперсной фазы;

T – температура раствора;

t– время, за которое происходит смещение частицы.

Таким образом, скорость броуновского движения коллоидных частиц изменяется лишь в зависимости от их радиуса и вязкости дисперсионной среды. При этом природа самой частицы на ее движение влияния не оказывает.

Если размеры и масса частиц дисперсной фазы превышают определенные пределы, вероятность взаимной компенсации ударов с различных направлений оказывается значительно выше.

Так, частицы размером 4 · 10 –6 м ÷ 5 · 10 –6 м совершают только небольшие колебательные движения около некоторого центра. При более крупных размерах частиц их броуновское движение в любом виде не наблюдается.

В связи с этим грубодисперсные системы не обладают молекулярно-кинетическими свойствами. Именно на этом отличии базируется классификация дисперсных систем на высокодисперсные и грубодисперсные.

Основной причиной движения крупных дисперсных частиц служит различие плотностей дисперсной фазы (ρ_ф) и дисперсионной среды (ρ_с). Если плотность дисперсной фазы больше (ρ_ф> ρ_с), то частицы постепенно оседают вниз под действием силы тяжести. Этот процесс называют седиментацией. Более легкие дисперсные частицы (ρ_с> ρ_ф), наоборот, постепенно всплывают вверх.Этот процесс называют обратной седиментацией.

Источник

Броуновское движение

Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.

2. Броуновское движение

Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.

Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.

Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.

Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.

4. Свойства броуновского движения и диффузии

Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:

2) от рода вещества, в котором эти процессы происходят;

3) от агрегатного состояния.

То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.

5. Практическое применение

Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.

Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.

Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.

6. Методические рекомендации учителям

1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.

2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.

3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.

4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!

5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.

Источник

Броуновское движение

Броуновским называют непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкости или газах, за счет воздействия молекул дисперсионной среды.

Мельчайшие частицы незначительной массы испытывают неодинаковые удары со стороны молекул дисперсионной среды; результирующая сила F, которая заставляет частицы двигаться, показана на рис. 9.1 жирной стрелкой. Направление и импульс этой силы непрерывно меняются, поэтому частицы совершают хаотическое движение.

Молекулы дисперсионной среды таким же образом действуют на частицы средне- и грубодисперсных систем. В связи со значительным размером частиц этих систем число ударов молекул резко увеличивается. По законам статистики подобное обстоятельство означает, что импульс действия сил со стороны молекул среды взаимно компенсируется, а значительная масса и инерция относительно крупных частиц способствует тому, что воздействие молекул остается без последствий. Поэтому броуновское движение наиболее интенсивно проявляется в отношении высокодисперсных систем.

Направление результирующей силы F (см. рис. 9.1), вызванной ударами молекул, и движение самих молекул все время изменяются. Определить эти изменения и связать их с молекулярно-кинетическими свойствами среды удалось в 1907 г. независимо друг от друга А. Эйнштейну и М. Смолуховскому.

Рис. 9.1. Воздействие молекул дисперсионной среды на частицу 1 дисперсной фазы.

Рис. 9.2. Сдвиг частиц.

В основу их расчетов был взят не истинный путь частиц дисперсной фазы, а сдвиг частиц (рис. 9.2). Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг будет определять среднеквадратическое смещение частицы, которое определяется по уравнению

, (9.2)

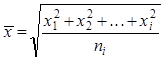
где х₁, х₂, x_i — сдвиг частиц за определенное время.

Теория броуновского движения исходит из представления о взаимодействии случайной силы f(τ), которая характеризует удары молекул, силы F_τ, зависящей от времени, и силы трения при движении частиц дисперсной фазы в дисперсионной среде со скоростью n. Уравнение случайного броуновского движения (уравнение Ланжевена) имеет следующий вид:

где m — масса частицы; η — коэффициент вязкости дисперсионной среды.

Для больших промежутков времени (τ >> m/η) инерцией частиц, т.е. членом m(dν/dτ), можно пренебречь. После интегрирования уравнения (9.2, а) при условии, что среднее произведение импульсов случайной силы равно нулю, находят среднее значение флуктуации (средний сдвиг):

(9.3)

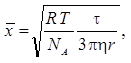
где τ — время; r — радиус частиц дисперсной фазы; N_A — число Авогадро.

В формуле (9.3) отражены параметры дисперсной фазы и дисперсионной среды: величина RT/N_A характеризует молекулярно-кинетические свойства дисперсионной среды, а η — ее вязкость; радиус частиц r — это параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой. Формула (9.3) подтверждена экспериментально.

Кроме поступательного возможно вращательное броуновское движение, характерное для двухмерных частиц и частиц неправильной формы (нитей, волокон, хлопьев и др.).

Средний сдвиг частиц различного размера за одну секунду в воздушной среде характеризуется значениями:

Максимальные значения
среднего сдвига, мкм 1,28 ∙ 10 3 0,168 0,0123

Средний сдвиг для частиц высокодисперсных систем размером 10 –3 — 10 –1 мкм (или 1—100 нм) может достигать нескольких миллиметров.

Броуновское движение наиболее ярко выражено у высокодисперсных систем, а его интенсивность зависит от дисперсности (см. рис. 1.2). Для среднедисперсных систем средний сдвиг составляет единицы или доли микрометров. Если размер частиц превышает 10 мкм, то броуновским движением можно пренебречь. Это обстоятельство является одним из факторов, ограничивающим верхний размер среднедисперсных систем значением 10 мкм.

Источник

Броуновское движение

Во второй половине ХХ века в научных кругах разгорелась нешуточная дискуссия о природе атомов. На одной стороне выступали неопровержимые авторитеты, такие как Эрнст Мах (см. Ударные волны), который утверждал, что атомы — суть просто математические функции, удачно описывающие наблюдаемые физические явления и не имеющие под собой реальной физической основы. С другой стороны, ученые новой волны — в частности, Людвиг Больцман (см. Постоянная Больцмана) — настаивали на том, что атомы представляют собой физические реалии. И ни одна из двух сторон не сознавала, что уже за десятки лет до начала их спора получены экспериментальные результаты, раз и навсегда решающие вопрос в пользу существования атомов как физической реальности, — правда, получены они в смежной с физикой дисциплине естествознания ботаником Робертом Броуном.

Еще летом 1827 года Броун, занимаясь изучением поведения цветочной пыльцы под микроскопом (он изучал водную взвесь пыльцы растения Clarkia pulchella), вдруг обнаружил, что отдельные споры совершают абсолютно хаотичные импульсные движения. Он доподлинно определил, что эти движения никак не связаны ни с завихрениями и токами воды, ни с ее испарением, после чего, описав характер движения частиц, честно расписался в собственном бессилии объяснить происхождение этого хаотичного движения. Однако, будучи дотошным экспериментатором, Броун установил, что подобное хаотичное движение свойственно любым микроскопическим частицам, — будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция.

Лишь в 1905 году не кто иной, как Альберт Эйнштейн, впервые осознал, что это таинственное, на первый взгляд, явление служит наилучшим экспериментальным подтверждением правоты атомной теор ии строения вещества. Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды. В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Однако, как бы ни мала была спора, в силу чисто случайных отклонений сначала она получает импульс со стороны молекулы, ударившей ее с одной стороны, затем — со стороны молекулы, ударившей ее с другой и т. д. В результате усреднения таких соударений получается, что в какой-то момент частица «дергается» в одну сторону, затем, если с другой стороны ее «толкнуло» больше молекул — в другую и т. д. Использовав законы математической статистики и молекулярно-кинетической теор ии газов, Эйнштейн вывел уравнение, описывающее зависимость среднеквадратичного смещения броуновской частицы от макроскопических показателей. (Интересный факт: в одном из томов немецкого журнала «Анналы физики» (Annalen der Physik) за 1905 год были опубликованы три статьи Эйнштейна: статья с теор етическим разъяснением броуновского движения, статья об основах специальной теор ии относительности и, наконец, статья с описанием теор ии фотоэлектрического эффекта. Именно за последнюю Альберт Эйнштейн был удостоен Нобелевской премии по физике в 1921 году.)

В 1908 году французский физик Жан Батист Перрен (Jean-Baptiste Perrin, 1870–1942) провел блестящую серию опытов, подтвердивших правильность эйнштейновского объяснения феномена броуновского движения. Стало окончательно ясно, что наблюдаемое «хаотичное» движение броуновских частиц — следствие межмолекулярных соударений. Поскольку «полезные математические условности» (по Маху) не могут привести к наблюдаемым и совершенно реальным перемещениям физических частиц, стало окончательно ясно, что спор о реальности атомов окончен: они существуют в природе. В качестве «призовой игры» Перрену досталась выведенная Эйнштейном формула, которая позволила французу проанализировать и оценить среднее число атомов и/или молекул, соударяющихся с взвешенной в жидкости частицей за заданный промежуток времени и, через этот показатель, рассчитать молярные числа различных жидкостей. В основе этой идеи лежал тот факт, что в каждый данный момент времени ускорение взвешенной частицы зависит от числа соударений с молекулами среды (см. Законы механики Ньютона), а значит, и от числа молекул в единице объема жидкости. А это не что иное, как число Авогадро (см. Закон Авогадро) — одна из фундаментальных постоянных, определяющих строение нашего мира.

Источник