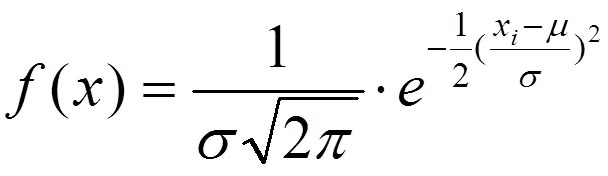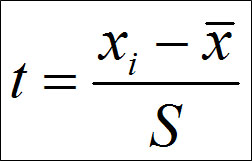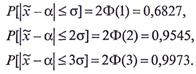Какими параметрами полностью характеризуется нормальный закон распределения
Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
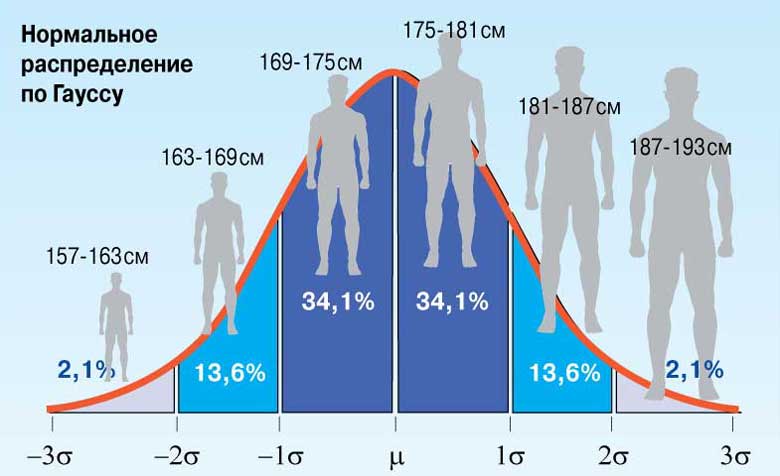
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
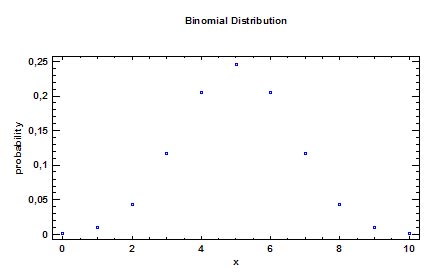
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z
Нормальный закон распределения
Нормальный закон распределения случайной величины
Значение для исследований в области физической культуры и спорта (ФКиС)
Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике. Причинами это являются:
Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.
История изучения нормального распределения
Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).
Дальнейшее развитие теория вероятностей получила в XVIII веке. В 1713 году была опубликована книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей. Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).
В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.
Эту задачу решил английский математик Абрахам де Муавр. В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую биномиальное распределение события, вероятность которого была равна 0,5 (рис.1). То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление формулы нормального распределения значительно упростило расчеты вероятностей событий.
В начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас обобщил результаты А. Муавра для произвольного биномиального распределения.
Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.
В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле одним из первых применил нормальный закон распределения случайной величины к анализу биологических и социальных процессов. Изучая распределение солдат американской армии по росту, Адольф Кетле обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).
В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.
Более подробно о методах статистической обработки данных рассказано в книгах:
Формула нормального распределения
Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.
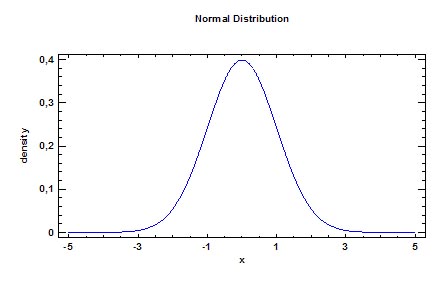
Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0 и σ=1. Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.2).
Рис.2. График плотности вероятностей нормального распределения при μ=0 и σ=1.
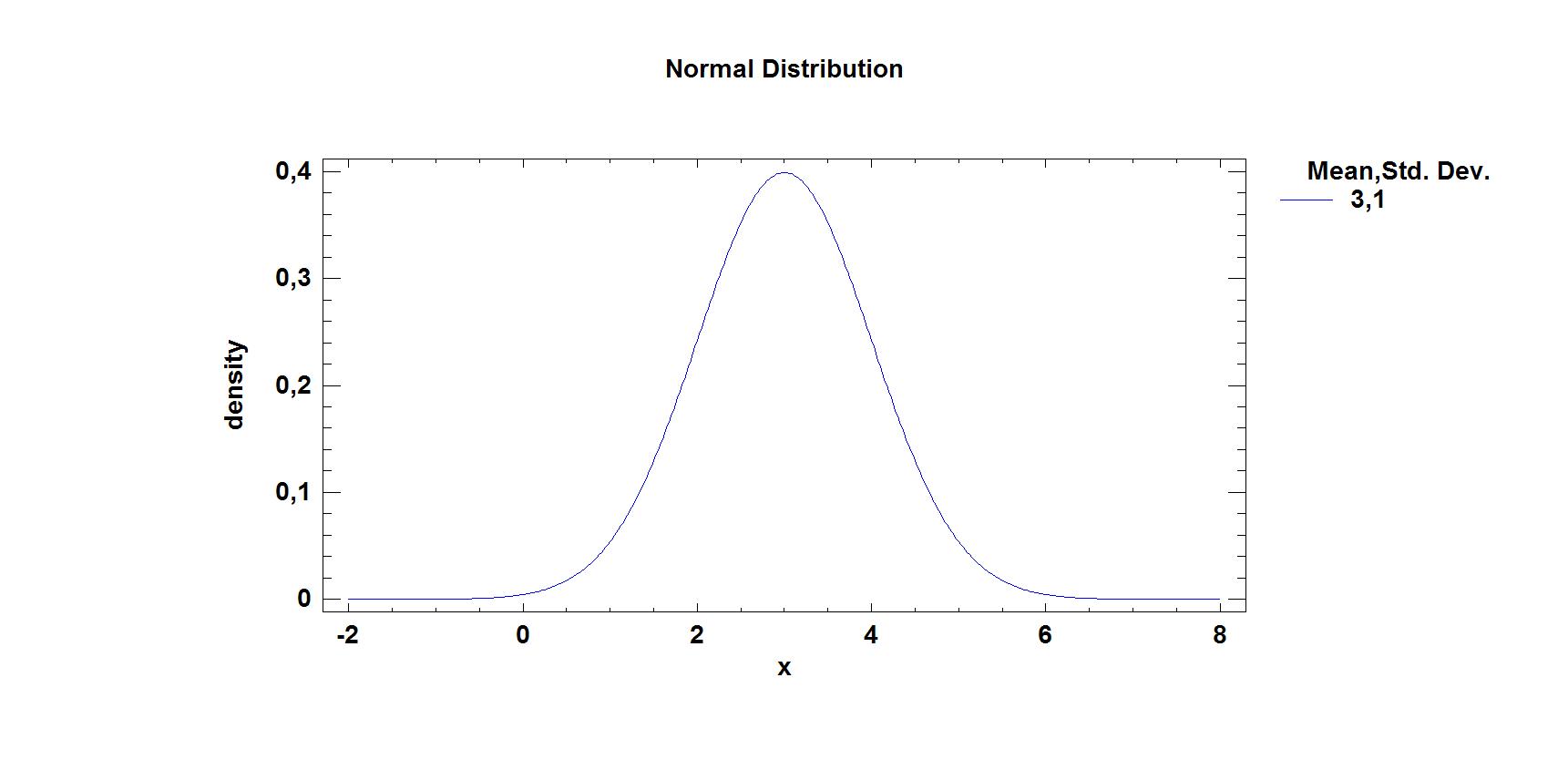
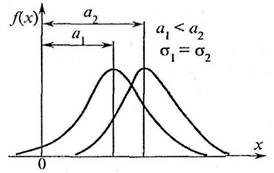
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при μ=3 график сместится вправо вдоль оси Х (рис.3).
Рис.3. График плотности вероятностей нормального распределения при μ=3 и σ=1.
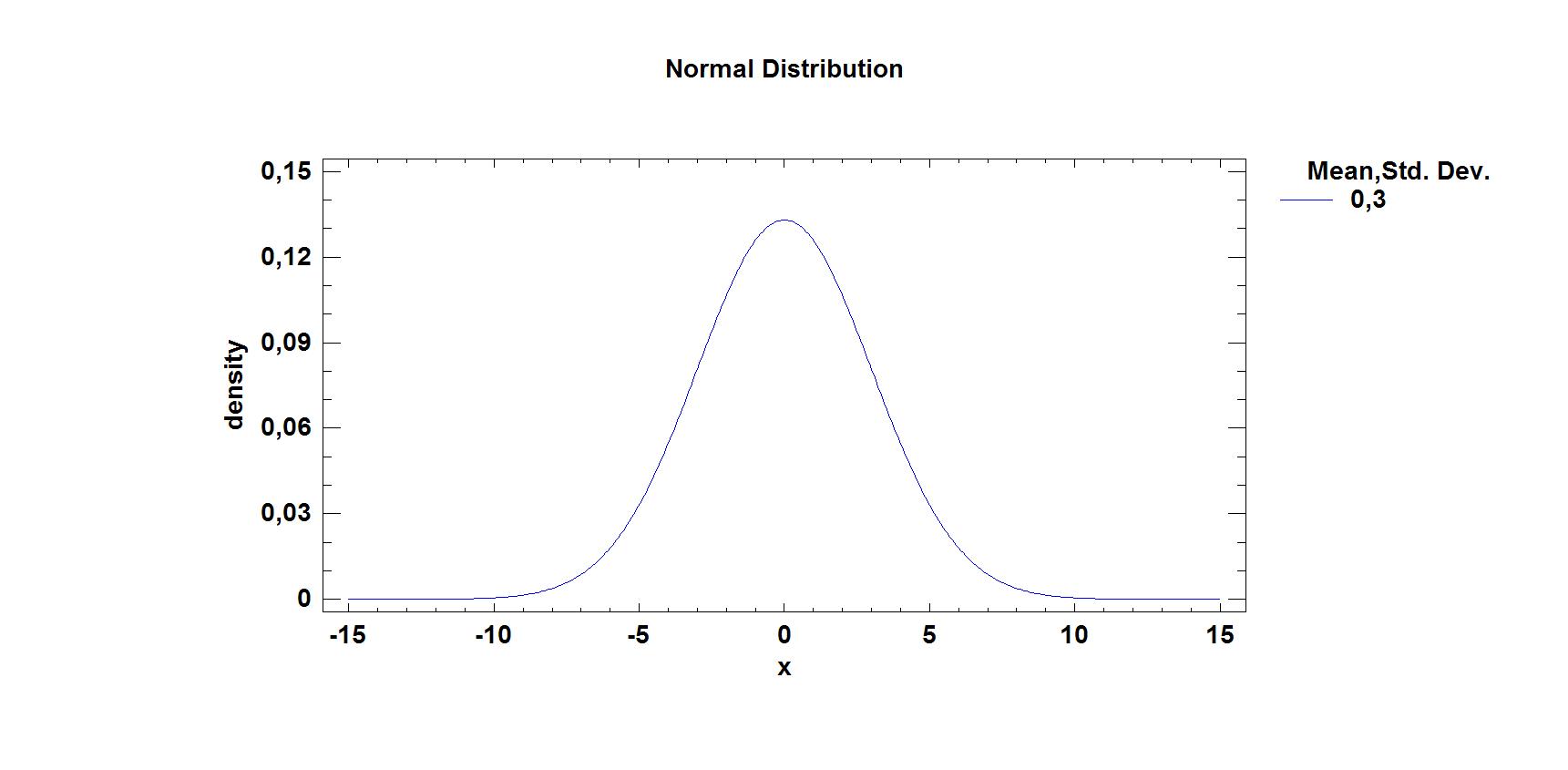
Рис.4. График плотности вероятностей нормального распределения при μ=0 и σ=3.
Свойства нормального распределения
Нормированное отклонение
В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».
Нормированное нормальное распределение
Рис.5. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.
Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры: µ=0; σ = 1 (рис.1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле:
Для нормированного нормального распределения характерно, что в интервал µ± σ попадают 68 % всех результатов, в интервал µ± 2σ попадают 95% всех результатов, в интервал µ± 3σ попадают 99 % всех результатов.
Критерии согласия
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.
Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).
Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
Нормальный закон распределения случайных величин



Нормальный закон распределения (закон Гаусса) играет особо важную роль в теории вероятностей и чаще других применяется в решении практических задач. Его главная особенность в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Например, сумма достаточно большого числа независимых (или слабо зависимых) случайных величин приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем больше случайных величин суммируется.
Экспериментально доказано, что нормальному закону подчиняются погрешности измерений, отклонения геометрических размеров и положения элементов строительных конструкций при их изготовлении и монтаже, изменчивость физико-механических характеристик материалов и нагрузок, действующих на строительные конструкции.
Распределению Гаусса подчиняются почти все случайные величины, отклонение которых от средних значений вызывается большой совокупностью случайных факторов, каждый из которых в отдельности незначителен (центральная предельная теорема).
Нормальным распределением называется распределение случайной непрерывной величины, для которых плотность вероятностей имеет вид (рис. 18.1).
Рис. 18.1. Нормальный закон распределения при а1
Вероятность попадания случайной величины, распределенной по нормальному закону, в интервал от х. до х, определяется выражением:
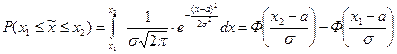
Следует заметить, что
При решении практических задач, связанных с распределением, часто приходится рассматривать вероятность попадания в интервал, симметричный относительно математического ожидания, если длина этого интервала 
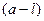
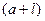
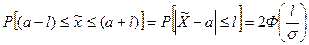
При решении практических задач границы отклонений случайных величин выражаются через стандарт, среднеквадратичное отклонение, умноженное на некоторый множитель, определяющий границы области отклонений случайной величины.
Принимая 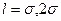
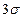
Эти формулы показывают, что если случайная величина имеет нормальное распределение, то вероятность ее отклонения от своего среднего значения не более чем на σ составляет 68,27 %, не более чем на 2σ — 95,45 % и не более чем на Зσ — 99,73 %.