какое поле называют вихревым
Вихревой характер магнитного поля
Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.
Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.
Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:
Определение вихревого поля также выполнимо другим способом.
Вихревое магнитное поле
Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.
Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:
При отсутствии токов вектор магнитной индукции B → представляется в виде градиента скалярного магнитного потенциала φ m :
Если имеются токи, то данное представление невозможно.
Различие между потенциальными и вихревыми полями
Основными уравнениями магнитного поля постоянных токов считаются выражения вида:
Произведем сравнение с основными уравнениями электростатики:
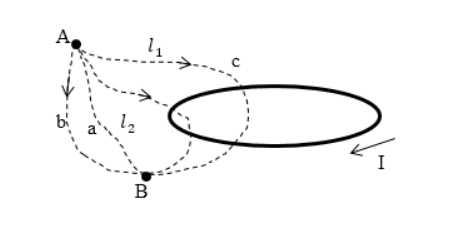
Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.
Известно значение r o t :
Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.
Следует задать нулевой потенциал в точке В :