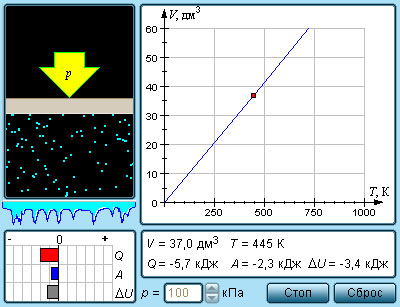
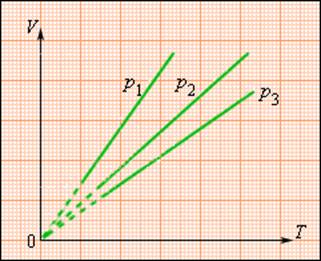
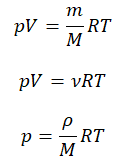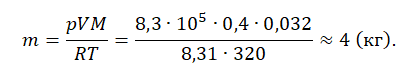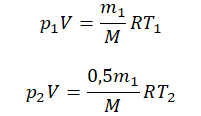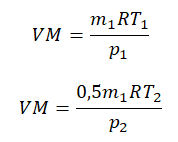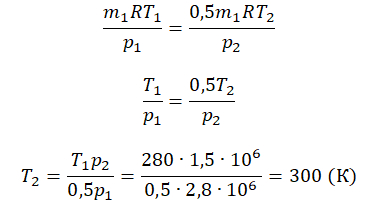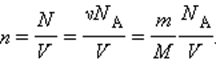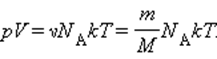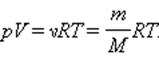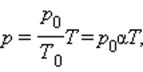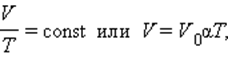Какое уравнение связывает основные параметры идеального газа

Какое уравнение связывает основные параметры идеального газа

где N_А — число Авогадро, k — постоянная Больцмана.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

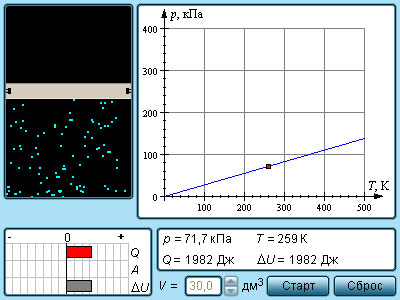
V= const => p/T = const — закон Шарля

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Источник

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза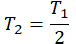
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул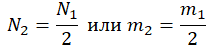
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы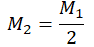
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Источник

Уравнение состояния идеального газа. Изопроцессы

Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.

Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:

Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.

Если имеется смесь невзаимодействующих газов, то формулу запишем как:

Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:

Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.

Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.

При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.

Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.

Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.

Источник

Уравнение состояния идеального газа. Изопроцессы

связывающее давление газа с его температурой и концентрацией молекул, получено в 3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

Здесь N – число молекул в сосуде, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:

называется уравнением состояния идеального газа.

Для одного моля любого газа это соотношение принимает вид:

Если температура газа равна T_н = 273,15 К (0 °С), а давление p_н = 1 атм = 1,013·10 5 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V₀, равный

V₀ = 0,0224 м 3 /моль = 22,4 дм 3 /моль.

Это утверждение называется законом Авогадро.

Для смеси невзаимодействующих газов уравнение состояния принимает вид

где ν₁, ν₂, ν₃ и т. д. – количество вещества каждого из газов в смеси.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Бенуа Клайпероном, в форме (*) оно было впервые записано Дмитрием Ивановичем Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.

Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.

Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.

Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.

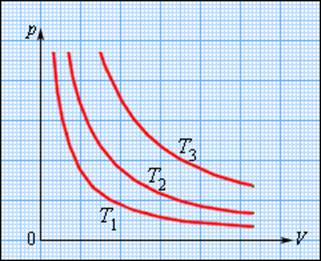
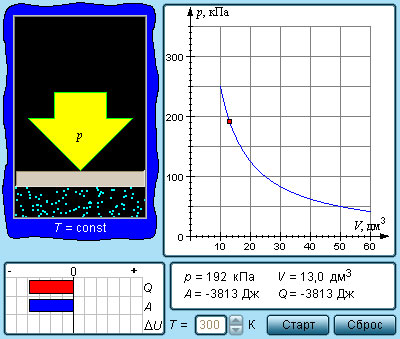
Изотермический процесс (T = const)

Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:

На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p

1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Робертом Бойлем (1662 г.) и независимо французским физиком Эдмом Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.

Изохорный процесс (V = const)

Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.

Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p

На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

Уравнение изохорного процесса может быть записано в виде:

Изобарный процесс (p = const)

Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Жозефом Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.

Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.

Источник

Уравнение состояния идеального газа

Математическая запись универсального газового закона проста:

Она содержит основные характеристики поведения газов: p, V и T — соответственно давление, объем и абсолютная температура газа (в градусах Кельвина), R — универсальная газовая постоянная, общая для всех газов, а n — число, пропорциональное числу молекул или атомов газа (так называемое число молей газа — см. Закон Авогадро).

Чтобы понять, как работает этот закон, давайте представим, что температура газа постоянна. В этом случае в правой части уравнения получается константа. Значит, произведение давления и объема при неизменной температуре оказывается неизменным. Повышение давления сопровождается уменьшением объема, и наоборот. Это не что иное, как закон Бойля—Мариотта — одна из первых экспериментально полученных формул, описывающих поведение газов. С другой стороны, при постоянном давлении (например, внутри воздушного шарика, где давление газа равно атмосферному) повышение температуры сопровождается увеличением объема. А это — закон Шарля, другая экспериментальная формула поведения газов. Закон Авогадро и закон Дальтона также являются следствиями универсального газового закона.

Этот закон представляет собой то, что в физике принято называть уравнением состояния вещества, поскольку он описывает характер изменения свойств вещества при изменении внешних условий. Строго говоря, этот закон в точности выполняется только для идеального газа. Идеальный газ представляет собой упрощенную математическую модель реального газа: молекулы считаются движущимися хаотически, а соударения между молекулами и удары молекул о стенки сосуда — упругими, то есть не приводящими к потерям энергии в системе. Такая упрощенная модель очень удобна, поскольку позволяет обойти очень неприятную трудность — необходимость учитывать силы взаимодействия между молекулами газа. И это себя оправдывает, поскольку в природных условиях поведение большинства реальных газов практически не отличается от поведения идеального газа — отклонения в поведении практически всех природных газов, например атмосферного азота и кислорода, от поведения идеального газа не превышают 1%. Это позволяет ученым спокойно включать уравнение состояния идеального газа даже в весьма сложные теоретические расчеты. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. (Заметьте, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. А дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия — то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов.) В будущем, по мере совершенствования теоретических методов, возможно, будут выведены более точные уравнения для описания состояния реальных газов с учетом их характеристик на молекулярном уровне.

* Эта формула была получена в 1874 году Д. И. Менделеевым путем объединения закона Авогадро и общего газового закона (pV/ T = const), сформулированного в 1834 году Б. П. Э. Клапейроном. Поэтому этот закон (в Европе, по крайней мере) принято называть законом Менделеева—Клапейрона. По существу, этот закон позволил ввести все ранее сделанные эмпирические заключения о характере поведения газов в рамки новой молекулярно-кинетической теории. (Примечание переводчика)

Источник

• через какое время делают повторное эко →