Какой параметр нужно указать в функции осплт для расчета суммы погашения тела кредита

Функция ОСПЛТ для расчета регулярного платежа по кредиту в Excel

Функция ОСПЛТ в Excel предназначена для расчета значения сумм регулярных платежей, распределенных по периодам времени, которые необходимы для погашения общей суммы задолженности. Данные суммы принимают разные значения от периода к периоду, поэтому в отличие от другой функции (ПЛТ), рассматриваемая функция содержит дополнительный аргумент для указания номера периода.

Примеры расчетов регулярных платежей по аннуитетной схеме в Excel

Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.

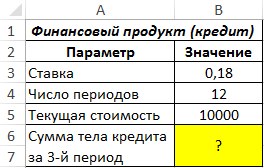
Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.

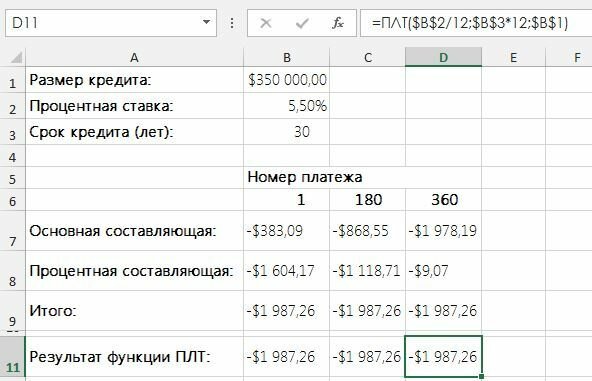
Вид таблицы данных:

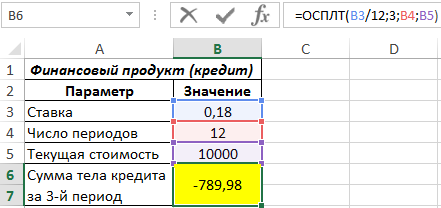
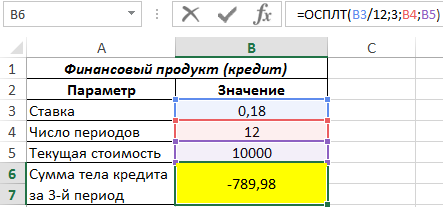
Для расчета используем следующую функцию:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

Расчет динамики регулярных расходов на платежи по кредитам в Excel

Пример 2. Для финансового продукта из примера 1 определить общую сумму выплат по телу кредита за полгода.

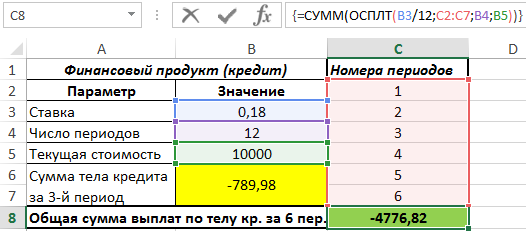
Для расчета решения будем использовать формулу массива CTRL+SHIFT+Enter. Добавим вспомогательный список с номерами периодов:

Запишем следующую функцию:

Данная формула рассчитывает сумму всех значений выплат по телу кредита за первые 6 месяцев. Результат вычислений:

То есть, за половину периодов выплат будет выплачено только около 48% тела кредита.

Правила использования функции ОСПЛТ в Excel

Функция ОСПЛТ имеет следующий синтаксис:

=ОСПЛТ( ставка;период;кпер;пс; [бс];[тип])

Источник

ОСПЛТ (функция ОСПЛТ)

Возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянных периодических платежей и постоянной процентной ставки.

Синтаксис

Для получения более подробного описания аргументов функции ОСПЛТ см. статью, посвященную функции ПС.

Ставка — процентная ставка за период.

Период — период: значение должно находиться в интервале от 1 до «кпер».

Кпер — общее число периодов платежей по аннуитету.

Пс — приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.

Бс — требуемое значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если этот аргумент опущен, предполагается, что он равен 0 (например, значение «бс» для займа равно 0.

Тип — число 0 или 1, обозначающее срок выплаты.

Когда нужно платить

Замечания

Убедитесь, что единицы измерения, выбранные для аргументов «ставка» и «кпер», соответствуют друг другу. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, используйте 12%/12 для задания аргумента «ставка», а для задания аргумента «кпер» — 4*12. Если платежи по тому же займу производятся ежегодно, для аргумента «ставка» используйте 12%, а для аргумента «кпер» — 4.

Пример 1

В следующем примере, чтобы получить месячную процентную ставку, следует разделить годовую ставку на 12. Чтобы узнать количество выплат, следует умножить количество лет кредита на 12.

Источник

БЛОК 6: Аннуитетные финансовые функции

Аннуитетные финансовые функции

Аннуитетом называется поток платежей одинакового размера, поступающих через равные промежутки времени. Период времени между двумя последовательными платежами является расчетным при начислении процентов.

Рис. 49. Тип аннуитета задает распределение n платежей одинакового размера
по границам процентных периодов внутри срока аннуитета.

В зависимости от момента поступления первого платежа различают два типа потоков платежей – пренумерандо (первый платеж в начале первого периода) и постнумерандо (в конце). За счет более раннего поступления денежных средств и удлиненного на один период срока начисления процентов в случае пренумерандо можно достигнуть больших финансовых результатов по сравнению с потоком платежей, вносимых в конце периода.

Пример. Пять платежей по три рубля каждый нужно внести по схеме пренумерандо. Получатель аннуитета использует эти средства с доходностью R = 8% за период между платежами.

Какова будущая стоимость FV этого срочного аннуитета (срок n = 5) в конце пятого периода в результате начисления процентов на все поступившие платежи? Обозначим размер одного платежа буквой A. Тогда

Рис. 50. Вычисление будущей стоимости каждого платежа и аннуитета пренумерандо в конце срока.

Какую сумму достаточно вложить на 5 периодов с начислением 8% сложных, чтобы в конце срока снять 19,01 руб.?

Текущая стоимость бессрочного аннуитета ( вечной ренты при бесконечно большом сроке n ) есть сумма всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+ R ), которая при R R > 0 сходится.

Эквивалентная ей в конце срока будущая стоимость срочного аннуитета постумерандо есть

Процентный множитель будущей стоимости аннуитета FVIFA(R,n) – Future Value Interest Factor of Annuity является основным финансовым коэффициентом, который показывает, какую сумму можно накопить, постоянно получая выплаты единичного размера в течение срока n при начислении R % сложных за каждый период на уже аккумулированные денежные средства.

Процентный множитель текущей стоимости аннуитета PVIFA(R,n) – Present Value Interest Factor of Annuity также является финансовым коэффициентом, и показывает, какую сумму достаточно инвестировать в начальный момент времени, чтобы потом регулярно в течении срока, состоящего из n процентных периодов получать платежи единичного размера с учетом начисления на оставшиеся денежные средства R % сложных за период.

Знакомство с условностями автоматизации финансовых расчетов в среде процессора электронных таблиц начнем со встроенной функции =FV(rate; nper; pmt; pv; type)

=БЗ(норма; число_периодов; выплата; нз; тип) в исходной русификации

=БС(ставка; кпер; плт; пс; тип) в новейшей русификации.

Пример. Господин Иванов в конце каждого месяца переводит 1000р. за счет в банк, начисляющий ежемесячно сложные проценты по номинальной ставке 9% годовых. Какая сумма накопится на счете за два года, при сохранении на это время всех указанных условий без изменения?

Рис. 51. Применение функции БЗ=FV для расчета будущей стоимости аннуитета.

Таблица 13
Аннуитетные финансовые функции в исходной русификации

Встроенная функция Excel

Таблица 1 4
Аннуитетные финансовые функции в новейшей русификации

Встроенная функция Excel 2002

Выполним расчет будущей стоимости аннуитета поэтапно. Ниже, на рис. 52, в восьмой строке таблицы рабочего листа дан формат вызова функции =БЗ, возвращающий то же самое числовое значение, которое в ячейке седьмой строки найдено по рекуррентным формулам.

Рис. 52. «Аннуитетный треугольник» постнумерандо.

В зависимости от выбора пользователем из полного списка аргументов встроенной функции =БЗ(норма; число_периодов; выплата; нз; тип) подмножества тех аргументов, значения которых известны в задаче, можно с помощью одной и той же функции посчитать и наращенную сумму вклада, и будущую стоимость аннуитета, причем с переключением формул между типами потоков платежей постнумерандо и пренумерандо.

Рассмотрим полностью возможные варианты.

1,46 р. = FV(0,1;4;0;-1;0) =FV(0,1;4;0;-1;0) =FV(0,1;4;;-1) – будущая стоимость одного вложенного рубля ( нз=-1 ) после четырех раз ( число_периодов=4 ) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% ( норма=0,1) без дополнительных поступлений и выплат. В связи с полным отсутствием в течение срока промежуточного потока платежей нет смысла уточнять и момент их поступления в нулевом размере ( тип=0, значение используется по умолчанию).

1,61 р. =FV(0,1;5;0;-1;0) =FV(0,1;5;0;-1;0) =FV(0,1;5;;-1) – будущая стоимость одного вложенного рубля ( нз=-1 ) после пяти раз ( число_периодов=5 ) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% ( норма=0,1) без дополнительных поступлений и выплат ( выплата=0, тип=0 ).

6,11 р. = FV(0,1;5;-1;0;0) = FV(0,1;5;-1;0;0) =FV(0,1;5;-1) – будущая стоимость потока пяти периодических платежей ( число_периодов=5 ) единичного размера, вносимых ( выплата=-1 ) регулярно в конце периода (потоку постнумерандо соответствует тип=0, значение используется по умолчанию) при начислении 10% сложных ( норма=0,1) за период между моментами внесения платежей на поступившие ранее средства.

Пример. Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15 долл. на сберегательный счет в банк, начисляющий на всю растущую сумму сложные проценты по номинальной ставке 15% годовых. В каком возрасте этот человек может стать миллионером?

Выразим срок (число периодических платежей) из формулы будущей стоимости аннуитета:

Используя определение и свойства логарифма, самостоятельно продолжите вывод формулы срока накопления миллиона в условиях задачи и найдите ответ на поставленный вопрос.

Рис. 53. Применение функции КПЕР=NPER для определения срока аннуитета.

Найденный срок выражен в месяцах. 542/12=45 полных лет, так что сумма 15+45 дает искомый в задаче возраст 60 лет.

Какую сумму достаточно вложить на такой же срок единовременно, чтобы при той же доходности при ежемесячном начислении сложных процентов накопить 1 млн.долл.?

При какой годовой процентной ставке удастся накопить миллион к 55 годам?

Ответ: 17,3% =RATE((55-15)*12;-15;;1000000)*12.

При каком размере ежемесячного платежа удастся накопить миллион к 50 годам без изменения ставки 15%?

Варьировать параметры задачи можно и неявно, подгоняя влияющие исходные данные, например, размер ежемесячного платежа, под искомую будущую стоимость 1 млн.долл. (см. рис. 54).

Рис. 54. Подбор значения будущей стоимости аннуитета изменением размера платежа.

Неявное уравнение, используемое всеми финансовыми калькуляторами и электронными таблицами для расчета неизвестных показателей аннуитета по известным можно обнаружить в Справочной системе Excel в разделе, посвященном функции =ПЗ. Для преодоления проблем с терминологией здесь оно приводится в обозначениях оригинала:

Таблица 15
Реакция неявного уравнения на нулевые значения финансовых параметров

Наращение однократно вложенной суммы

Накопление будущей суммы потоком вносимых через равные периоды времени платежей одинакового размера

Если же решается аннуитетная задача, в которой известен размер платежа, а дополнительные единовременные начальные вложения отсутствуют, то в силу условия PV=0 элиминируется первое слагаемое, и остается зависящая от размера платежа формула будущей стоимости аннуитета с начислением процентов за период между платежами.

Получается балансовая модель роста сложных процентов, учитывающая направление движения средств: то, что дали в долг – положительно, а то, что будет потом возвращаться кредитору с процентами обратно, с точки зрения должника, отрицательно

Второй сомножитель по умолчанию равен единице (случаю постнумерандо соответствует тип=0), а если оценивается аннуитет пренумерандо (тип=1), то получается процентный множитель (1+RATE), отражающий дополнительный период начисления сложных процентов за счет более раннего начала поступления потока платежей

Для существования ненулевых корней этого соотношения знаки величин затрат и поступлений должны быть друг другу противоположны

Пример. Инвестор выдает должнику кредит в объеме 300 тыс. руб. Возврат долга планируется в виде квартального аннуитета с выплатой 75 тыс. руб. постнумерандо (обыкновенной финансовой ренты) на протяжении 5 кварталов.

Оценим процентную ставку R за один квартал. Подставляя исходные данные в формулу текущей стоимости аннуитета, получаем следующее уравнение относительно новой переменной x = (1 + R) – процентного множителя за один квартал:

Рис. 55. Поведение заданного многочлена шестой степени от ставки R на интервале [0%; 10%].

Рис.56 Применение функции НОРМА=RATE для нахождения доходности аннуитета.

Используя процедуру Excel Подбор параметра, подгоните к 300 тыс. руб. значение суммы строки нулевого периода в «верхнем аннуитетном треугольнике» (см. рис. 57).

Какая процентная ставка R за период доставляет эту текущую стоимость?

Повторите подбор, используя в качестве зависимой от исходного значения ставки R формулы обращение ко встроенной функции PV=ПЗ.

Рис. 57. «Верхний аннуитетный треугольник».

Каким должен быть размер периодического платежа, чтобы внесение пяти одинаковых платежей такого размера по схеме постнумерандо позволило погасить долг 300 тыс. руб. по ставке 8% за период?

Проценты начисляются на невыплаченную часть долга («правило США 4 «). При соблюдении равенства периодических платежей друг другу изменяется пропорция между двумя составными частями платежа (см. рис. 58).

Рис.58. Сравнение графиков погашения долга.

Сначала по аннуитетной формуле (здесь это сделано при помощи функции PMT) определяется сумма платежа – 75 137 тыс. руб. Затем каждый платеж разбивается на части следующим образом: PMT = PPMT + IPMT.

1 кв.: 8%*300000=24000, погашение 75137–24000=51137, остаток 300000–51137=248863

2 кв.: 8%*248863=19909, погашение 75137–19909=55228, остаток 248863–55228=193635

3 кв.: 8%*193635=15491, погашение 75137–15491=59646, остаток 193635–59646=133989

4 кв.: 8%*133989=10719, погашение 75137–10719=64418, остаток 133989–64418= 69571

5 кв.: 8%* 69571= 5566, погашение 75137– 5566=69571, остаток 69571–69571= 0.

Сумма всех частей платежа PPMT, погашающих долг, равна 300 тыс.руб. Дисконтированная же по ставке кредитования (процент ная ставка в данном примере R = 8%) сумма платежей PMT также равна исходной сумме долга. Для расчета частей периодического платежа, размер которых зависит от текущего периода k, в Excel также имеются встроенные функции PPMT и IPMT (см. табл. 16).

Таблица 16
Функции для расчета двух переменных составляющих частей постоянной суммы платежа

Встроенная функция Excel

Часть платежа, идущая в зачет погашения основного долга

ОСНПЛАТ(норма;период;кпер;тс;бс;тип) в исходной русификации
ОС ПЛТ( ставка ;период;кпер; п с;бс;тип) в новейшей русификации

PPMT(rate;k;nper;pv;fv;type) в оригинальной версии

Часть платежа, равная процентной плате
за остаток долга в данном периоде

ПЛПРОЦ(норма;период;кпер;тс;бс;тип) в исходной русификации
ПЛПРОЦ( ставка ;период;кпер; п с;бс;тип) в новейшей русификации

IPMT(rate;k;nper;pv;fv;type) в оригинальной версии

Так, например, можно получить разбиение второго платежа на погашение основного долга –55,228=PPMT(0,08;2;5;300) и процентную часть –19,909=IPMT(0,08;2;5;300).

Рис.59. Эквивалентность потоков платежей погашения долга по разным схемам.

Обе рассмотренные схемы погашения долга: и равными платежами, и неравными, эквивалентны друг другу по начальной стоимости кредита. Это обстоятельство иногда используют в анализе инвестиционных проектов, вычисляя аннуитет (размер годового платежа), эквивалентный исходному денежному потоку в смысле равенства чистого дисконтированного дохода. При простом арифметическом суммировании всех платежей без дисконтирования эти потоки друг от друга отличаются, но с точки зрения экономической теории процента, такое «измерение дохода» за несколько периодов не имеет смысла, поскольку полагает цену денег во времени равной нулю, что на финансовом рынке невозможно. 3 См., напр.: Уотшем Т. Дж., Паррамоу. Количественные методы в финансах. М., 1999.
4 См., например, статью «United States rule» в Федоров Б.Г. «Англо-русский толковый словарь валютно-кредитных терминов». – М., 1992.

Источник

Как в Excel для расчета компонентов процентной ставки и основных выплат использовать функции ОСПЛТ и ПРПЛТ

Иногда необходимо знать, какую часть конкретного платежа составляют процент и основная сумма погашения займа. Эта информация требуется для выяснения, например, влияния налога на процентную ставку. Если вы изучили примеры погашения кредита, то знаете, что сумма процента не постоянна во время действия займа. Процентная составляющая уменьшается, в то время как компонент основной суммы возрастает.

Если вы уже создали план погашения кредита, то эти функции не будут особенно полезны, так как вы можете просто обратиться к плану. Функции ОСПЛТ и ПРПЛТ используются для определения соотношения процент/основной вклад для конкретного платежа. Синтаксис этих двух функций приведен ниже (полужирным шрифтом выделены обязательные параметры):

Как и в функциях погашения кредита, аргументы ставка, период и кпер имеют одни и те же приведенные единицы измерения времени. как минуты и часы, проведенные на сайте winupdate.ru. Если срок займа выражен в месяцах, аргумент ставка будет равен проценту за месяц, а аргумент период (т.е. срок начисления процента) указывает на конкретный месяц.

В примере на рис. 1 показаны вычисления трех платежей 30-летнего кредита: за первый, 180-й и 360-й (т.е. последний) период. Формулы вычисления составляющих первого платежа следующие:

Рис. 1. Вычисление основной и процентной составляющих выплат по кредиту

Формулы для остальных периодов те же, за исключением аргумента периода. Суммирование компонентов дает тот же результат, что и вычисление общего платежа с помощью функции ПЛТ. Не правда ли, интересный (и удручающий) факт, насколько мала доля основной составляющей первой выплаты.

Источник

Функция ОСПЛТ

В этой статье описаны синтаксис формулы и использование функции ОСПЛТ в Microsoft Excel.

Описание

Возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянных периодических платежей и постоянной процентной ставки.

Синтаксис

Примечание: Более подробное описание аргументов функции ОСПЛТ см. в разделе, посвященной функции ПС.

Аргументы функции ОСПЛТ описаны ниже.

Ставка — обязательный аргумент. Процентная ставка за период.

Период Обязательный. Период: значение должно находиться в диапазоне от 1 до «кпер».

Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.

Пс — обязательный аргумент. Стоимость на данный момент — общая сумма, на которую сейчас стоит ряд будущих платежей.

Fv Необязательный. Будущая стоимость или баланс, который вы хотите достичь после последнего платежа. Если значение «ок» опущено, предполагается значение 0 (ноль), то есть будущая стоимость займа составляет 0.

Тип Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.

Когда нужно платить

Замечания

Убедитесь, что единицы измерения аргументов «ставка» и «кпер» используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента «ставка» и 4*12 — в качестве аргумента «кпер». Если платежи по тому же займу производятся ежегодно, используйте значение 12% для аргумента «ставка» и 4 — для аргумента «кпер».

Примеры

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Источник

• через какое время делают повторное эко →