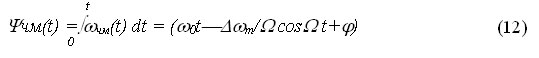Какой параметр является информационным при амплитудной модуляции

Амплитудная модуляция

Амплитудная модуляция (AM) является наиболее простым и распространенным способом изменения параметров носителя информации. При AM огибающая амплитуда гармонического колебания (переносчика) изменяется по закону, совпадающему с законом изменения передаваемого сообщения, частота же и начальная фаза колебания поддерживаются неизменными. Поэтому для амплитудно-модулированного колебания выражение (3.1) можно заменить следующим:

Характер огибающей A(t) определяется видом передаваемого сообщения.

Основным параметром амплитудно-модулированного колебания является коэффициент модуляции, когда модулирующая функция является гармоническим колебанием:

Огибающую модулированного колебания при этом можно представить в виде:

где Q — частота модуляции; у — начальная фаза огибающей; кam — коэффициент пропорциональности; —

амплитуда изменения огибающей (рис. 3.2).

Рис. 3.2. Колебание, модулированное по амплитуде гармонической

Отношение — называется коэффициентом модуляции. Таким образом, мгновенное значение модулированного колебания:

Источник

Теория радиоволн: аналоговая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции

Источник

Амплитудная модуляция на пальцах

В недавней статье «Амплитудная модуляция произвольного сигнала» её автор довольно сумбурно попытался представить своё понимание формирования спектра при амплитудной модуляции. Но отсутствие иллюстраций и избыток математики с привлечением интегральных преобразований помешало сообществу понять мысли автора и оценить статью по достоинству; в то время как тема это достаточно простая — и рассмотреть которую мы попробуем ещё раз, на этот раз с картинками и привлечением Wolfram Mathematica.

Итак, идея амплитудной модуляции состоит в том, чтобы передавать низкочастотный сигнал — голос или музыку — модулируя высокочастотный (несущий) сигнал, многократно превышающий слышимый диапазон и занимающий узкую полосу частот в радиоэфире. Сама модуляция осуществляется простым умножением сигнала на несущий:

Здесь у нас в качестве несущей выступает синусоида с частотой 5:

А сам сигнал — с частотой 1:

Можно заметить, что сигнал смещён вверх и имеет только положительные значения. Это не случайно и является обязательным условием для возможности последующего его корректного восстановления. Как же его восстановить? Очень просто! Нужно сдвинуть фазу промодулированного сигнала на 90 градусов (операция, известная как преобразование Гильберта), и посчитать корень из суммы квадратов модулированного и преобразованного сигналов:

В более простом (но грубом) варианте преобразование Гильберта можно заменить задержкой сигнала на четверть периода несущий частоты, а итоговый сигнал дополнительно отфильтровать фильтром низких частот. В ещё более простом варианте можно вообще не считать корней и квадратов, а отфильтровать сигнал по абсолютному значению (что и применяется обычно в радиоприёмниках).

Теперь посмотрим, что у нас происходит со спектрами. Посчитаем преобразование Фурье от несущей:

Так как дельта-функция Дирака не является функцией в классическом смысле, её график нельзя построить стандартным способом; поэтому сделаем это вручную, используя общепринятое начертание:

Ожидаемо получили ту же частоту, что и в начальной формуле. Наличие ещё одной такой же частоты, но со знаком минус, не случайно — это явление называется Hermitian symmetry и является следствием того, что рассматриваемая функция сугубо действительная и в комплексном представлении имеет нулевую мнимую компоненту. Отсутствие мнимых компонент в спектре после преобразования обусловлено тем, что изначально наши функции ещё и чётные (симметричные относительно нуля).

Теперь сделаем преобразование Фурье для самого сигнала:

Здесь мы дополнительно получили дельта-функцию Дирака в центре координат — вследствие наличия в сигнале постоянной составляющей, которая не имеет колебаний по определению — что позволяет её рассматривать как нулевую частоту.

Что же будет со спектром, если их перемножить? Посмотрим:

Из теории мы знаем, что умножение во временном домене равносильно свертке в частотном (и наоборот, что широко используется при FIR-фильтрации). А поскольку один из подвергаемых свёртке сигналов состоял только из одной (положительной и отрицательной) частоты, то в результате свёртки мы получили просто линейный перенос сигнала вверх по частоте (в обе стороны). И так как симметрия осталась, сигнал у нас по-прежнему не имеет мнимой компоненты.

Приведём его теперь к комплексному (аналитическому) виду, обнулив отрицательную область частот:

и сделаем обратное преобразование Фурье:

Так как функция теперь комплексная, для построения её графика необходимо отдельно извлечь действительную и мнимую компоненты:

Теперь у нашего сигнала появилась мнимая компонента, представляющая собой сдвинутый на 90 градусов исходный сигнал. Это будет более очевидным, если представить полученную функцию в тригонометрическом виде:

Пока не очень очевидно. Попробуем упростить:

Теперь больше похоже на правду — и как видим, функция нашего исходного сигнала тоже упростилась. Попробуем её вернуть к оригинальному виду:

Множитель 1/2 появился не случайно — ведь обнулив половину спектра, мы соответственно и уменьшили мощность сигнала. Ну а теперь, имея модулированный комплексный сигнал, мы можем взять и этот модуль посчитать:

Модуль комплексного числа как раз и считается через корень суммы квадратов мнимого и действительных компонентов. И отсюда понятно, почему кодируемый сигнал должен состоять только из положительных значений — если он будет включать отрицательные значения, то после восстановления они также станут положительными, что и называется перемодуляцией:

Восстановление сигнала также возможно и при помощи квадратурного гетеродина — когда модулированный сигнал снова умножается на несущую частоту, но на этот раз — комплексную:

За счёт того, что комплексная частота в частотной области имеет только один импульс без дублирования его в отрицательной области частот — то в результате свёртки мы получим линейный перенос спектра, при которой отрицательная часть спектра встанет обратно в центр, а положительная — сдвинется ещё дальше, и её останется только отфильтровать фильтром нижних частот.

Заключение

Как видим, в рассмотрении амплитудной модуляции через преобразовании Фурье нет ничего сложного; если же рассматривать её исключительно на школьном уровне, то достаточно вспомнить, что произведение (несущей) суммы (представление сигнала в виде тригонометрического ряда) равнозначно сумме произведений (каждого члена ряда по отдельности на несущую частоту) — и, соответственно, каждое такое произведение раскладывается на сумму двух синусоид по уже озвученной автором исходной статьи формуле.

Внимательный читатель также мог заметить, что раз в результате модуляции мы получили симметричный относительно несущей частоты спектр — значит, имеет место быть избыточность данных и можно оставить только одну боковую полосу, сократив тем самым занимаемую полосу частот в радиоэфире. Такая технология действительно имеется, но это — уже совсем другая история.

Источник

Что такое модуляция и разновидности модулированных сигналов?

Общие сведения о модуляции

Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.

В результате модуляции сигналы переносятся в область более высоких частот.

Использование модуляции позволяет:

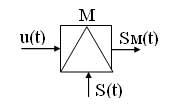
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

При модуляции на вход модулятора подаются сигналы:

u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);

S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w₀ или f₀);

Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.

В качестве несущего сигнала может использоваться:

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.

1. Виды аналоговой модуляции:

2. Виды импульсной модуляции:

Амплитудная модуляция

Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение амплитуды несущего сигнала по закону:

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Вынесем Um за скобки:

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

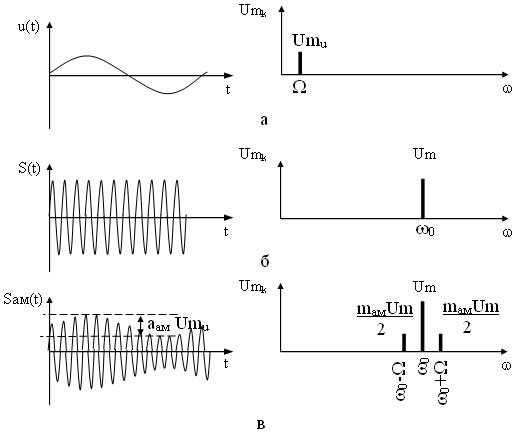
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

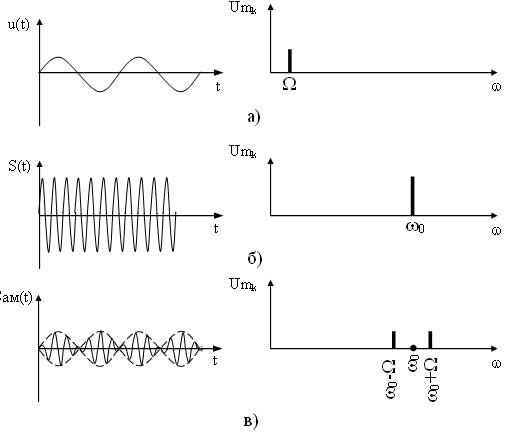
Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?₀—? называется нижней боковой составляющей, а на частоте ?₀ + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

Ширина спектра для данного сигнала будет определятся

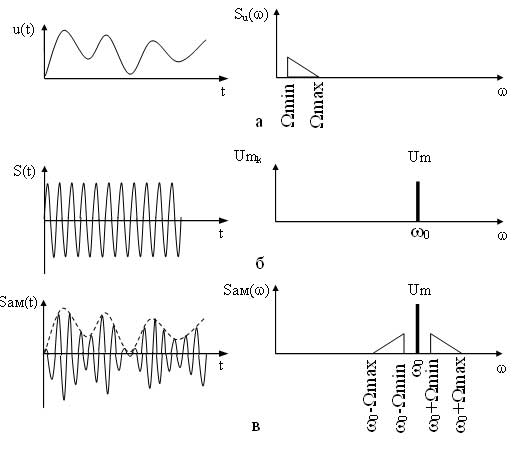
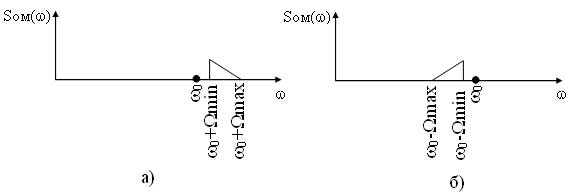
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Ширина спектра для данного сигнала будет определятся

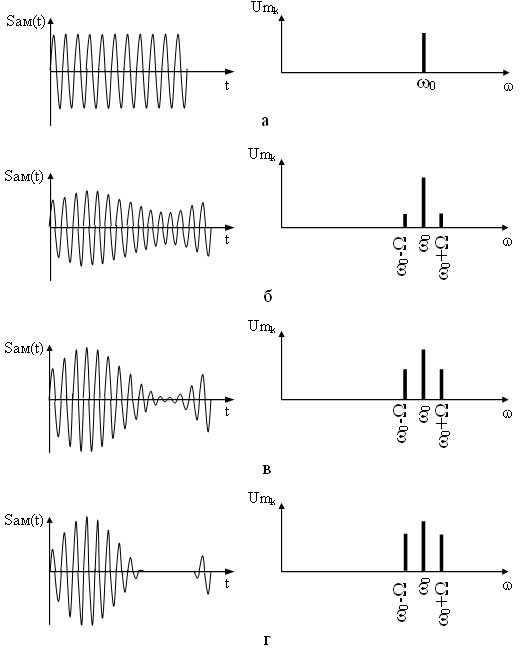
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

Недостатками этой модуляции являются:

Амплитудная модуляция нашла широкое применение:

Балансная и однополосная модуляция

Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.

Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.

Частотная модуляция

Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение частоты несущего сигнала по закону:

где а_чм — коэффициент пропорциональности частотной модуляции.

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

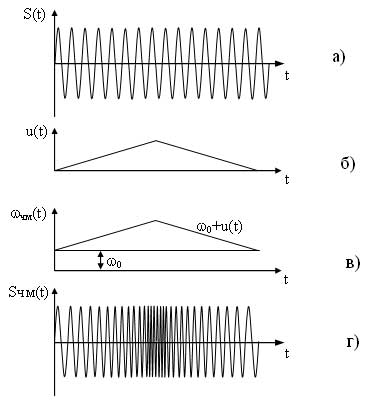
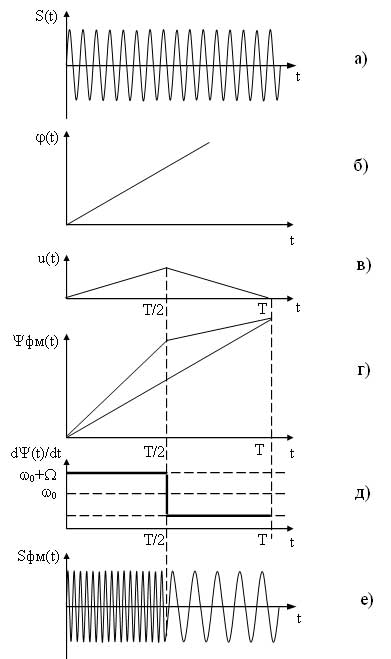
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

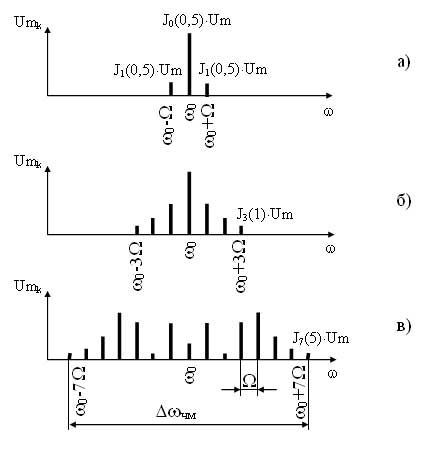
Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

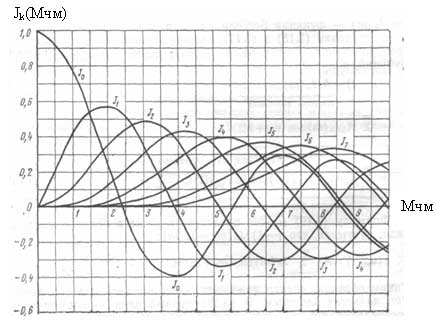
где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

Достоинством частотной модуляции являются:

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

Фазовая модуляция

Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение мгновенной фазы несущего сигнала по закону:

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

Произведение а_фмUm_u?=??_m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

Ширина спектра ФМ сигнала определяется выражением:

Достоинствами фазовой модуляции являются:

Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

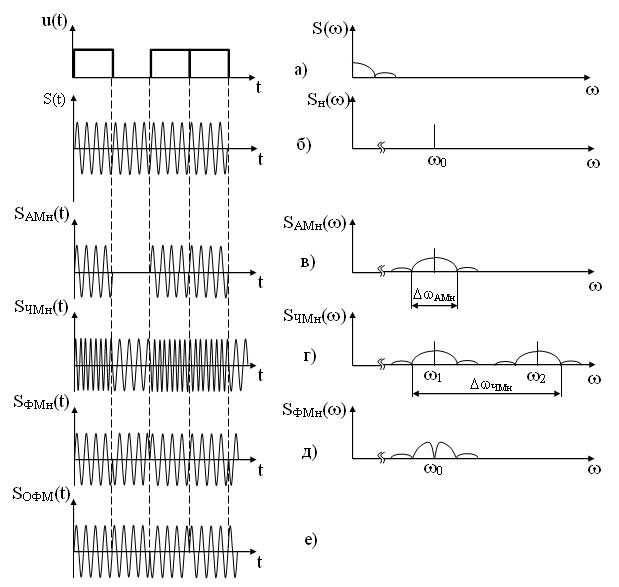
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

Импульсная модуляция

Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.

Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:

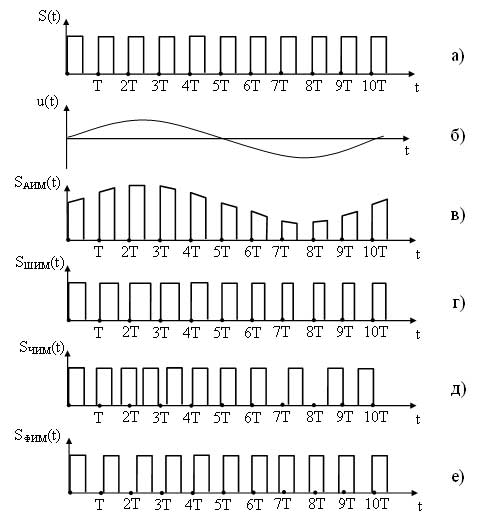
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.

При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).

При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).

При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).

При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.

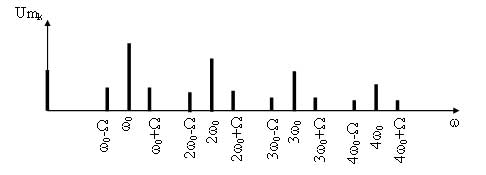
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.

Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.

Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f₀ =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.

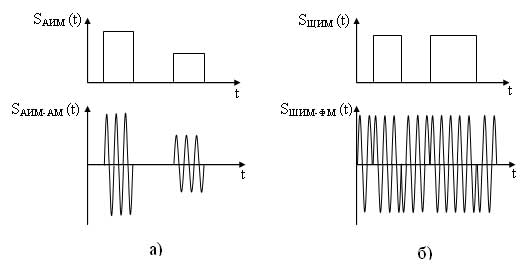
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.

Источник