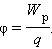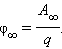какую работу совершает поле при
Какую работу совершает поле при
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда и две различные траектории перемещения пробного заряда из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение 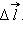
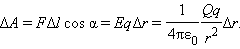 |
Таким образом, работа на малом перемещении зависит только от расстояния между зарядами и его изменения Δ. Если это выражение проинтегрировать на интервале от = 1 до = 2, то можно получить
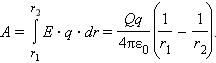 |
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов 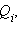
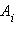
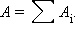
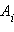
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
|
Потенциал φ является энергетической характеристикой электростатического поля.
Работа 12 по перемещению электрического заряда из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| 12 = p1 – p2 = φ1 – φ2 = (φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
Потенциал φ∞ поля точечного заряда на расстоянии от него относительно бесконечно удаленной точки вычисляется следующим образом:
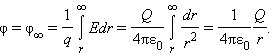 |
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд совершил малое перемещение 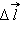
| Δ12 = Δ = (φ1 – φ2) = – Δφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
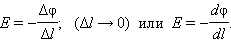 |
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь – координата, отсчитываемая вдоль силовой линии.