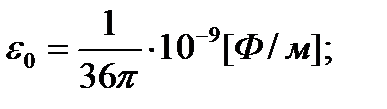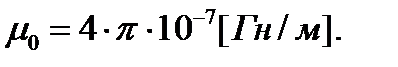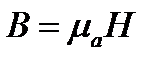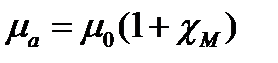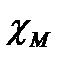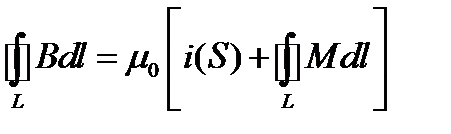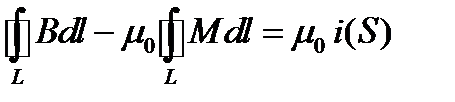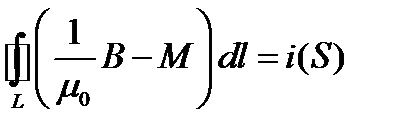Классификация сред и их электрические параметры
Параметры и классификация сред



Для характеристики сред, в которых протекают электромагнитные процессы, в простейшем случае вводят три скалярных параметра:
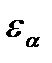
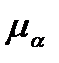

Для идеальной среды (вакуума) проводимость равна нулю, а диэлектрическая и магнитная проницаемость являются постоянными величинами и называются постоянными вакуума (мировыми постоянными):
Часто среды характеризуют относительными проницаемостями:
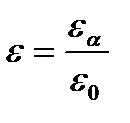
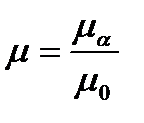
Параметры среды (материала) связаны с векторами ЭМП уравнениями, которые называют материальными или уравнениями
состояния:
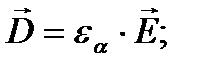
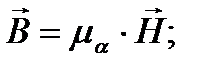
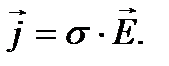
Последнее уравнение –закон Ома в дифференциальной форме. При наличии стороннего источника плотность полного тока будет равна:
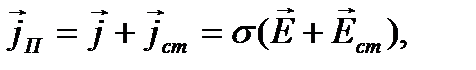
где 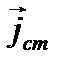
Параметры среды в общем случае являются не числом, а функцией координат, времени, модуля и вектора напряженности поля, например, для диэлектрика 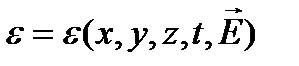
μ= μ(x, y, z, t, 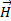
Среда, параметры которой во всех точках одинаковы, называется однородной, в противном случае –неоднородной. Примером однородной среды может служить вакуум, полистирол, феррит и т.д. Неоднородной средой является, например, атмосфера Земли.
Если параметры среды с течением времени не меняются, то она называется средой с постоянными параметрами, или стационарной. Если это не выполняется, то среда спеременнымипараметрами, т. е. нестационарная. Например, атмосфера Земли является средой с переменными параметрами.
Среда, параметры которой не зависят от напряженности поля, называется линейной, в противном случае –нелинейной. Примером нелинейной среды служит среда, в которой распространяется излучение мощного лазера.
Если параметры среды не зависят от направления векторов поля, то среда называется изотропной, в противном случае –анизотропной. Примеры анизотропных сред: плазма, ионосфера, подмагниченный феррит. Подмагниченный феррит называют еще гиротропной средой.
В последние годы значительное внимание уделяется искусственным средам с пространственной дисперсией, называемымкирильными.Такие среды удобны при создании диэлектрических линзовых антенн, радиопрозрачных обтекателей для антенн и другого, подробнее [5]. В дальнейшем будем рассматривать класс линейных сред.
Классификация сред.
Среды по макроскопическим параметрам делят на изотропные и анизотропные, линейные и нелинейные, однородные и неоднородные.
Изотропной называют среду, физические свойства которой одинаковы по всем направлениям в каждой точке p. В среде, изотропной по отношению к электрическому полю, элементарные электрические моменты диполей ориентированы преимущественно параллельно напряженности электрического поля.
Линейной называют среду, физические свойства которой не зависят от величины векторов поля. В линейной и изотропной по отношению к электрическому полю среде вектор P пропорционален и параллелен вектору E: 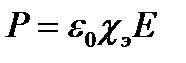
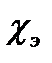
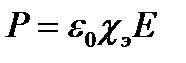
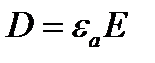
где 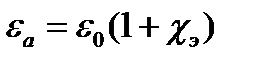
Нелинейной называют среду, физические свойства которой зависят от величины векторов поля. В нелинейной изотропной по электрическому полю среде вектор P нелинейно зависит от величины напряженности электрического поля и может иметь нелинейный гистерезисный характер. В последнем случае такие вещества называют ферроэлектриками или сегнетоэлектриками.
Анизотропной называют среду, физические свойства которой в точке p различны по различным направлениям. В анизотропной среде вектор P непараллелен векторам E и D. Поэтому в общем случае каждая составляющая вектора D зависит от трех составляющих вектора E:Х3
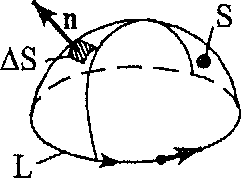
| Рис. 1 Контур и опирающаяся на него поверхность |
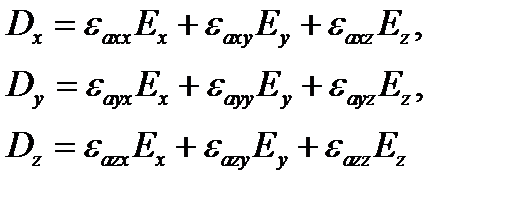
где 
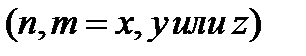
Вещества по своим магнитным свойствам разделяются на изотропные и анизотропные, линейные и нелинейные, однородные и неоднородные.
В изотропном магнетике под воздействием внешнего магнитного поля элементарные магнитные моменты ориентируются преимущественно параллельно вектору В. При этом вектор М и, значит, вектор Н параллельны вектору В. В линейном изотропном магнетике вектор М пропорционален и параллелен вектору В. Это выражение записывают в виде:
где 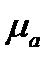
Так как 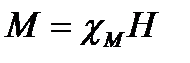
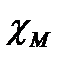
Изотропные линейные магнетики делятся на две группы — парамагнетики и диамагнетики. У парамагнетиков векторы М и Н примерно совпадают по направлению, поэтому 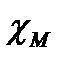
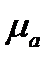
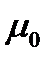
К нелинейным магнетикам относятся ферромагнетики. Ферромагнетиками являются ферромагнитные металлы (железо, кобальт, кадмий и их сплавы между собой и с другими неферромагнитными элементами) и ферриты. У ферромагнетиков зависимости составляющих вектора М от соответствующих составляющих вектора Н имеют нелинейный гистерезисный характер. В ферромагнетике при уменьшении до нуля значения Н сохраняется остаточная намагниченность. Тело, сохраняющее длительное время остаточную намагниченность, называется постоянным магнитом.
В анизотропном линейном магнетике векторы М, Ни В не параллельны. Примером анизотропных магнетиков являются ферриты, находящиеся в постоянном магнитном поле, в них для переменного во времени ЭМ поля магнитная проницаемость становится тензором.
В магнитном поле векторные линии магнитной индукции B непрерывны, они не имеют ни начала, ни конца. Поэтому магнитный поток через любую замкнутую поверхность равны нулю (принцип непрерывности магнитного потока):

Причиной этого является отсутствие в природе магнитных зарядов, которые могли бы стать источниками магнитного поля аналогично тому, как электрические заряды являются источниками электрического поля. Магнитное поле порождается электрическими токами, а линии B замыкаются вокруг последних.
Опытным путем установлено, что вектор B и постоянные токи (протекающие по замкнутым контурам) в вакууме связаны с законом полного тока для вакуума
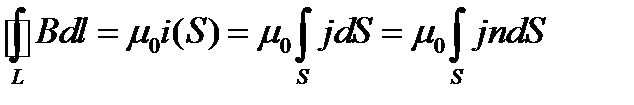
где L-произвольный замкнутый контур, 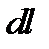
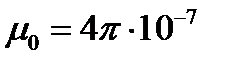
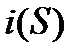
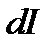
Магнитные поля, порождаемые одним и тем же проводником с одинаковым током, перемещенным в различные вещества, различаются. Объясняется это тем, что в любом веществе существуют замкнутые элементарные электрические токи, возникающие за счет вращения отрицательно заряженного электрона по орбите вокруг положительно заряженного ядра атома; за счет этого образуются элементарные рамки тока, обладающие магнитными моментами. Кроме этого, электрон вращается вокруг своей оси, образуя спиновый магнитный момент. При воздействии на вещество внешнего магнитного поля в ориентировке этих магнитных моментов возникает некоторая упорядоченность. В единице объема вещества появляется магнитный момент. Этот процесс называют намагничиванием, а вещества, способные намагничиваться, называют магнетиками. Магнитное состояние вещества при этом характеризуется с помощью вектора намагничивания M– магнитного момента, которым обладает единица объема вещества в точке p.
Применим выражение закона полного тока к магнетикам. Появление дополнительных токов в магнетиках должно учитываться в правой части этого выражения дополнительным слагаемым 
Если обозначить здесь
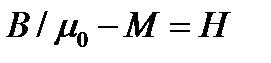
то получим закон полного тока, справедливый для любого вещества при постоянном во времени токе:
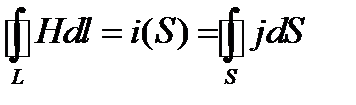
В общем случае ЭМ поле в среде наводит (индуцирует) токи проводимости — вторичные токи с плотностью 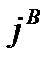
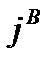
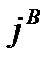
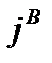
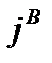
Зависимость (функция) 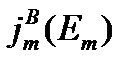
Имеем закон Ома в дифференциальной форме:

Величина 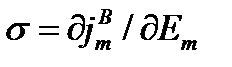
В случае, когда 
У всех веществ а отлично от нуля. Но значения 

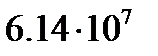

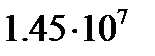

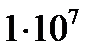

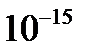

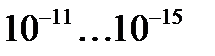
8. Известно, что ток в цепи с омическим сопротивлением сопровождается выделением джоулева тепла. Чтобы поддерживать ток, необходимо ввести в цепь сторонний источник.
Наличие 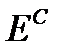
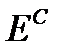
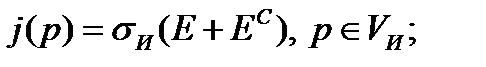
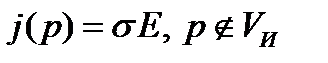
где 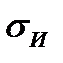
Если здесь величину 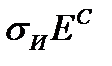
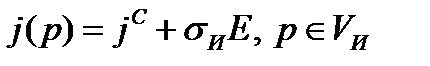
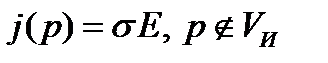
Закон Ома (13), или (14), считают справедливым и в нестационарном случае.
Как материальный объект ЭМ поле может быть охарактеризовано совокупностью четырех векторов E(p,t) и В(p,t), D(p,t) и Н(p,t), являющихся непрерывными функциями положения обыкновенной точки наблюдения р и времени t. Обыкновенной точкой р считают такую точку, в окрестности которой физические свойства среды непрерывны. При переходе точки наблюдения р через поверхность, ограничивающую материальное тело, векторы поля и их производные могут иметь разрывы. При этом точки р относятся к особым точкам. Характер разрывов устанавливается при изучении граничных условий. Пока граничные условия не изучены, особые точки из рассмотрения нами исключаются.
В линейных изотропных средах векторы Е, D и В, Н связаны выражениями:
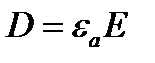
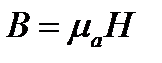
Вторичный ток: 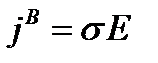
Выражения (15) и (16) называют материальными уравнениями (уравнениями состояния) линейной изотропной среды.
В вакууме отсутствуют частицы вещества, поэтому 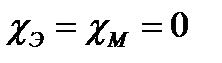
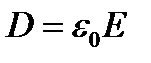
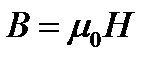
т.е. диэлектрическая и магнитная проницаемости вакуума равны соответственно электрической и магнитной постоянным 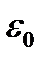
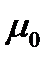
На практике часто пользуются безразмерными относительными диэлектрической и магнитной проницаемостями 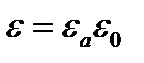
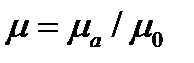
Дата добавления: 2015-08-11 ; просмотров: 3233 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Классификация сред
Свойства среды по отношению к электромагнитному полю определяются параметрами ε, μ и σ. Различают следующие среды:
линейные, в которых параметры ε, μ и σ не зависят от величины электрического и магнитного полей, и
нелинейные, в которых параметры ε, μ и σ (или хотя бы один из них) зависят от величины электрического или магнитного поля.
Все реальные среды, по существу, являются нелинейными. Однако при не очень сильных полях во многих случаях можно пренебречь зависимостью параметров ε, μ и σ от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна. В дальнейшем будут рассматриваться только линейные среды.
В свою очередь, линейные среды делятся на однородные и неоднородные, изотропные и анизотропные.
Однородныминазывают среды, параметры ε, μ и σ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров ε, μ или σ является функцией координат, называют неоднородными.
Если свойства среды одинаковы по разным направлениям, то среду называют изотропной. Соответственно среды, свойства которых различны по разным направлениям, называют анизотропными. В изотропных средах векторы Р и Е, D и Е, а также М и Н, В и Н параллельны, а в анизотропных средах они могут быть не параллельными. В изотропных средах ε, μ и σ –скалярные величины. В анизотропных, по крайней мере, один из этих параметров является тензором. К анизотропным средам относятся, например, кристаллические диэлектрики, намагниченная плазма и намагниченный феррит. В кристаллическом диэлектрике и намагниченной плазме тензором является диэлектрическая проницаемость ε. При использовании декартовой системы координат в общем случае тензор диэлектрической проницаемости может быть записан в виде матрицы

Чтобы записать уравнение (1.20) в проекциях на оси декартовой системы координат х, у, z, нужно раскрыть правую часть уравнения (1.20) по обычным правилам умножения матриц. В результате получим:

Непараллельность векторов D и Е (а также Р и Е) в анизотропной среде объясняется тем, что в общем случае направление возникающего в результате поляризации анизотропной среды вторичного электрического поля, созданного связанными зарядами вещества, составляет некоторый угол (отличный от 0 и p) с направлением первичного электрического поля.
В намагниченной ферромагнитной среде тензором является магнитная проницаемость. В общем случае в декартовой системе координат тензор магнитной проницаемости может быть представлен в виде
При этом форма уравнения (1.17) сохраняется:
Записывая уравнение (1.23) в проекциях на оси декартовой системы координат х, у, z, приходим к формулам, аналогичным (1.21).
Удельная проводимость σ также может быть тензорной величиной. Для таких сред закон Ома в дифференциальной форме (1.9) принимает вид j= ||σ||·E.