Колебательная система с распределенными параметрами

Колебательная система с распределенными параметрами

В этом случае колебания стержня описываются (пренебрегая инерцией вращения стержня при изгибе) волновым уравнением:

Решение этого уравнение дает формулу для определения основной частоты камертона

Поскольку анализ колебательной системы с распределенными параметрами связан со значительными вычислительными трудностями, особенно если учитывать нелинейное трение, различные внешние воздействия и рассматривать камертоны сложной формы, то целесообразно заменить такую систему некоторой эквивалентной колебательной системой с сосредоточенными параметрами. Однако нужно отметить, что такая замена допустима лишь при анализе определенных параметров в ограниченной области частот.

Дифференциальное уравнение эквивалентной системы имеет следующий вид:

Консольно-закрепленный невесомый упругий стержень, колеблющийся в вязкой среде, с массой на свободном конце, является упрощенной физической моделью ветви рассматриваемого камертона.

Собственная частота колебаний такой системы определяется формулой (2).

В таблице 2 приведены значения корректирующего фактора для целого ряда значений

Часто используются не свободные, а нагруженные камертоны, на концах ветвей которых расположены какие-либо грузы (постоянные магниты, детали магнитопровода и т.п.).

Резонансная частота такого камертона без учета изгиба ветвей определяется по формуле

На практике можно считать J_r = 0, тогда

В нагруженных камертонах позиционная ошибка, вызванная действием возмущающей силы, приложенной к центру тяжести груза, может иметь большую величину. Она подобна возвращающей силе маятника:

Так как имеет малые отклонения, можно считать, что возмущающая сила будет равна

Тогда собственную частоту колебаний можно записать в виде

где определяется по формуле (1).

Воздействие температуры на частоту колебаний камертона можно оценить по формуле

Одним из наиболее распространённых осцилляторов является струна. Собственная частота колебаний её определяется формулой

Удлинение струны при растяжении равно

При постоянных и г частота колебаний в струне в соответствии с формулой (3) зависит только от напряжения в струне.

Основным фактором, вызывающим изменение частоты колебаний струны, является изменение её рабочей длины. Это изменение может произойти в результате нагрева струны или основания, вытягивания струны измеряемым усилием. Температурная погрешность струны по частоте может быть определена зависимостью вида

По заданным коэффициентам линейного расширения и можно определить необходимые длины деталей, составляющих основание.

Применяется также способ термокомпенсации путём крепления струны к стойке из биметалла.

На точность работы преобразователей, основанных на струнных осцилляторах, большое влияние оказывает вид закрепления концов струны. Существует множество способов заделки концов струн.

Обзор устройств контроля забойных параметров и рассмотрение вопроса развития электромеханических колебательных систем позволяют сделать следующие выводы: во-первых, существующие устройства контроля технологических и геометрических забойных параметров работают ненадёжно и при этом имеют большую погрешность, во-вторых, в существующей литературе отсутствуют данные об использовании инфранизкочастотных механических преобразователей для контроля забойных параметров в процессе бурения скважин. В связи с этим авторы считают необходимым на основе проведённых исследований показать возможности инфранизкочастотных механических преобразователей и подчеркнуть актуальность работ по созданию на их основе устройств для измерения параметров бурения непосредственно на забое скважины.

Источник

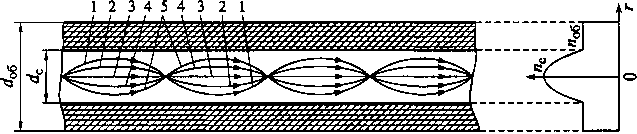
Для уменьшения величины модовой дисперсии применяют многомодовые градиентные световоды (рис. 10.17), в которых показа­тель преломления сердцевины изменяется вдоль радиальной коор­динаты r по нелинейному закону. Траектории лучей в неоднородной среде сердцевины являются криволинейными.

Рис. 10.17. Ход лучей и распределение показателя преломления в градиент­ном многомодовом ВС

На рис. 10.17 пока­зан ход лучей и распределение показателя преломления в градиентном многомодовом ВС. Траектории лучей, пересекающих ось сердцевины под большими углами, имеют большую длину, однако они проходят в области сердцевины, где показатель преломле­ния меньше, а фазовая скорость волн выше. Это приводит к выравниванию времен распространения различных мод в ВС, что существенно снижает величину модовой дисперсии. Лучшие об­разцы градиентных многомодовых ВС имеют коэффициент широ-кополосности более 1,2. 1,5 ГГц • км.

КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.1. Резонансные линии. Их свойства

Колебательные системы являются одними из наиболее распро­страненных элементов электронных схем. В частотном диапазоне, где длины электромагнитных волн намного превосходят линейные размеры элементов электронных схем, применяются колебав тельные системы с сосредоточенными параметрами. Они реализу­ются в виде колебательных контуров, представляющих последовательное или параллельное соединение сосредоточенных индуктивностей, емкостей и сопротивлений. Колебательный процесс в контуре представляет непрерывный, периодический обмен энер­гией между электрическим полем, сосредоточенным в конденса­торе, и магнитным полем катушки индуктивности.

С повышением частоты уменьшается длина волны и соответ­ственно должны уменьшаться размеры элементов колебательных систем с сосредоточенными параметрами. На частотах выше не­скольких сотен мегагерц они становятся настолько малыми, что возникают серьезные трудности при их изготовлении и примене­нии. Кроме того, с ростом частоты в сосредоточенных элементах увеличиваются тепловые потери (за счет скин-эффекта) и потери на излучение. Поэтому на достаточно высоких частотах (на деци­метровых и более коротких волнах) применяют преимущественно колебательные системы из элементов с распределенными парамет­рами. Характерными примерами таких систем являются короткие отрезки длинных линий, называемые резонансными линиями, и полые резонаторы, образованные замкнутыми металлическими оболочками.

Резонансными линиями называются короткие отрезки длинных линий, которые используются в качестве колебательных контуров с распределенными параметрами. Достоинствами резонансных ли­ний являются высокие электрические показатели, эксплуатацион­ная надежность и простота конструкции. Применяются они в ос­новном на дециметровых и сантиметровых волнах, так как в мет­ровом диапазоне они приобретают недопустимо большие размеры.

Основанием для использования отрезков длинной линии в ка­честве колебательных систем является характер зависимости вход­ного сопротивления линии от ее длины в режиме стоячих волн. Входное сопротивление идеальной разомкнутой линии, длина ко­торой равна четному числу четвертей длины волны, согласно вы­ражению (9.15) и рис. 9.16 равно бесконечности. При небольшом укорочении линии или при понижении частоты ее реактивное вход­ное сопротивление приобретает индуктивный характер, а при не­значительном увеличении длины линии или частоты — емкостной характер. Поведение линии такой длины с изменением частоты аналогично поведению параллельного колебательного контура.

Если длина разомкнутой линии равна нечетному числу четвер­тей длины волны, то ее входное сопротивление становится рав­ным нулю. Поведение такой линии при незначительном измене­нии частоты аналогично поведению последовательного колеба­тельного контура (см. рис. 9.15).

Зависимость входного сопротивления от длины идеальной короткозамкнутой линии имеет тот же характер, что и для разомкну­той линии, но отличается сдвигом на четверть длины волны (см. рис. 9.18, а). Поэтому короткозамкнутая линия с изменением час­тоты ведет себя как параллельный контур при длине, равной нечетному числу четвертей длины волны, и как последовательный контур — при длине, равной четному числу четвертей длины волны.

Отмеченные свойства отрезков линий широко используются в электронных схемах для дециметровых и сантиметровых волн. Так, линии с длиной, кратной четверти длины волны, используются в качестве колебательных контуров и согласующих трансформато­ров. Отрезки линий с длиной, не кратной четверти длины волны, применяются в качестве реактивных сопротивлений.

Входное сопротивление разомкнутой и короткозамкнутой ли­нии с потерями имеет конечные по величине активную и реак­тивную составляющие (см. рис. 9.16 и 9.18, б). В этом случае пове­дение указанных отрезков длинной линии эквивалентно поведе­нию реальных колебательных контуров с потерями.

Резонансные линии, соответствующие последовательному или параллельному колебательному контуру, принято характеризовать эквивалентными параметрами этого контура, к которым относят­ся резонансные частоты, характеристическое сопротивление, ре­зонансное сопротивление и добротность. Эти параметры позволя­ют проводить расчеты электронных схем, в составе которых ис­пользуются резонансные линии, точно так же, как и с примене­нием колебательных контуров.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Для повышения добротности разомкнутых полосковых резона­торов (особенно полуволновых) их изгибают в виде подковы (см. рис. 11.4, в). Сближение противофазных по электрическому полю торцов резонатора существенно снижает потери на излучение. Однако при уменьшении зазора sмежду торцами растут потери в проводнике резонатора (из-за эффекта близости). Поэтому суммарные потери резонатора на излучение и в проводниках при определенной величине зазора sимеют минимум, а добротность — максимум. Подковообразные разомкнутые резонаторы при оптимальной ширине зазора sимеют добротность на 55 % выше, чем прямолинейные, и являются более компактными.

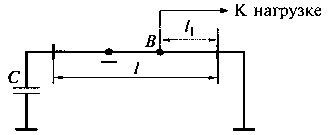
Рис. 11.5. Схема неполного включе­ния нагрузки в короткозамкнутый полосковый резонатор

Расчет параметров эквивалентного колебательного контура полосковых прямоугольных резонаторов осуществляется так же, и для двухпроводных резонансных линий с помощью соотношений, приведенных в подразд. 11.2.

Полная добротность нагруженного резонатора (добротность эквивалентного контура) определяется из соотношения 1/Q_экв = 1/Q₀ + 1/Q_вн, где Q₀— собственная добротность ненагруженного резонатора; Q_вн — внешняя добротность резонатора, обусловленная потерями мощности в нагрузке.

Для заданной конструкции полоскового резонатора величину полной добротности Q_экв можно регулировать, изменяя внешнюю добротность Q_вн, обусловленную отбором мощности из резона в нагрузку. Это осуществляется с помощью неполного включения нагрузки в резонатор. Для примера на рис. 11.5 приведена схема неполного включения нагрузки в короткозамкнутый полосковый резонатор на несимметричной полосковой линии, один конец которого нагружен на укорачивающий конденсатор С.

б

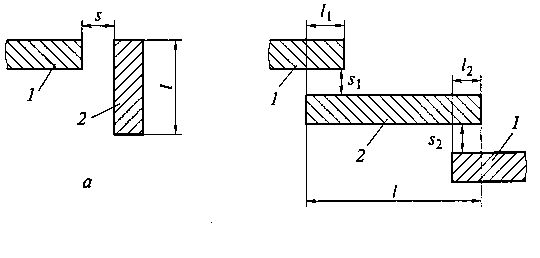
Рис. 11.6. Варианты включения полоскового резонатора в линию схеме двух- (а) и четырехполюсника (б): 1— полосковая линия; 2— резонатор

Благодаря этому конденсатору резонатор имеет длину l 17 18

Источник

Системы с распределенными параметрами. Длинные линии

Наряду с системами с сосредоточенными параметрами в радиотехнике используются также системы с распределенными параметрами. К ним относятся антенны и длинные линии. Кроме того, используемые в диапазонах дециметровых и сантиметровых волн колебательные системы также являются системами с распределенными параметрами.

Под длинной линией понимают систему двух параллельных цилиндрических проводников (двухпроводная линия) (рис. 2.20) или концентрических цилиндрических проводников (коаксиальная линия) (рис. 2.21).

__________6_ _

При этом линейные размеры системы вдоль направления распространения электромагнитной волны больше или сопоставимы с длиной волны, а в поперечном направлении много меньше длины волны (1 > Л, d « X). В диапазонах метровых, дециметровых и сантиметровых волн нашли широкое распространение плоские (полосковые) линии передачи. В этом случае один проводник выполняется в виде узкой тонкой полоски и располагается параллельно другому проводнику, выполненному в виде широкой пластины, которая заземляется. Полосковую линию такого типа называют несимметричной (рис. 2.22 а).

Используются также симметричные полосковые линии. В них узкая металлическая полоска располагается симметрично между двумя заземленными металлическими пластинами (рис. 2.22 б). Пространство между проводниками в коаксиальной и полосковой линиях обычно заполняют диэлектриком.

тонными параметрами линии). Пренебрегая сопротивлениями проводов линии и проводимостью утечки диэлектрика, имеющегося между ними, бесконечно малый отрезок dx (рис. 2.23) можно представить эквивалентной схемой (рис. 2.24).

Кроме того, из рис. 2.24 видно, что в соответствии с первым правилом Кирхгофа разность тока в сечениях х и х + dx равна току, текущему через конденсатор емкостью С_п dx. Следовательно,

Разность напряжений в сечениях х и (х + dx) равна падению напряжения на катушке индуктивностью L_odx, откуда сле

Уравнения (2.49) и (2.50) впервые были получены при создании теории проволочного телеграфа и получили название телеграф ных уравнений. Продифференцировав уравнение (2.49) и (2.50) по і и приравняв найденные из них смешанные производные

получим волновые уравнение для силы тока в длинной линии:

Аналогично, продифференцировав (2.51) по х и приравняв смешанные производные

получим волновое уравнение для силы тока в длинной линии:

Аналогично продифференцировав (2.49) по t, а (2.50) — по х и приравняв смешанные производные

получим волновое уравнение для напряжения между проводами линии:

Уравнения (2.52) и (2.53) математически эквивалентны. Путем подстановки можно убедиться в том, что этим уравнениям удовлетворяет любая функция типа

Функция / при знаке «минус» в аргументе описывает волну, бегущую в положительном направлении оси х со скоростью v, при знаке «плюс» — волну, бегущую в противоположном направлении. С волнами напряжения и тока связаны соответственно волны электрического и магнитного полей, существующих в пространстве между проводами линии. Для двухпроводной линии

Подставив значения L и С в формулу для г, получим:

Такой же результат получается не только для двухпроводной, но также для полосковой и коаксиальной линий. Электромагнитные волны распространяются в длинных линиях с той же скоростью, что и в однородном изотропном диэлектрике. Провода линии при этом играют роль канала, который обеспечивает передачу электромагнитной энергии в определенном направлении и не позволяет ей рассеиваться в стороны.

Характер волнового процесса в длинной линии, т. е. конкретный вид функции / зависит от условий возбуждения волн. Так, если к левому концу линии подключен генератор синусоидальных высокочастотных колебаний, а линия имеет бесконечную протяженность, то в ней будет существовать синусоидальная электромагнитная волна, частота которой определяется частотой колебаний генератора. В этом случае бегущая волна имеет вид:

где К = — = ——волновое число.

Подставив (2.54) в (2.49) и проинтегрировав левую и правую части получившегося уравнения по / при любом фиксированном х, получим:

При сравнении (2.54) и (2.55) видим, что при чисто бегущей волне сила тока и напряжение в линии меняются синфазно. Следовательно, отношение

і в любой момент времени в любом сечении линии одинаково:

Величина Z_o, зависящая от геометрии линии, является одним из важных электрических параметров линии без потерь, называемым волновым сопротивлением. Она характеризует среднюю за период мощность, уносимую электромагнитной волной от генератора высокочастотных колебаний.

По форме это выражение эквивалентно закону Джоуля— Ленца для цепи переменного тока:

Из (2.56) следует, что если в качестве нагрузки длинной линии использовать активное сопротивление, равное Z_o, то вся мощность электромагнитной волны будет поглощаться нагрузкой, т. е. в линии будет сущест вовать чисто бегущая волна. Такую нагрузку называют согласованной.

Если нагрузка не является согласованной, она поглощает лишь часть мощности, другая часть отражается от нее. В линии, кроме бегущей волны, существует также стоячая волна. В том случае, когда нагрузка отражает всю падающую на нее мощность, в линии устанавливается чисто стоячая волна. Этот режим работы линии реализуется, если сопротивление нагрузки равно нулю (режим короткого замыкания) или неограниченно велико (режим холостого хода).

Благодаря резонансным свойствам отрезков линий при холостом ходе или коротком замыкании на концах они используются в качестве колебательных систем в диапазонах дециметровых или сантиметровых волн.

Источник

Кинематическое возбуждение

При движении точки подвеса по гармоническому закону S = Sq cos?2t: чувствительность системы к перемещению

фаза вынужденных колебаний груза по отношению к фазе возмущающих колебаний

чувствительность системы к скорости по перемещению

чувствительность системы к ускорению по перемещению

Система с двумя степенями свободы

Если колебательная система имеет две массы М и М₂ и одну, две к<, к₂ или три пружины, соединяющие их между собой, то такая система называется двухмассовой (рис. 2.4)

Внешняя сила приложена к массе М. Математическое описание этой системы довольно громоздко, поэтому для конкретных практических приложений прибегаем к их упрощению. В инженерной практике представляет инт ерес использование двухмассовой системы

для устранения колебаний машин и сооружений с помощью динамических поглотителей колебаний (гасителей).

составим выражения для собственных частот системы:

На основании этого выражения можно сделать следующие выводы:

Таким образом, если настроить вторую парциальную систему (К₂, М₂) на ее частоту п₂, то она будет совершать колебания по зако-(Ра] „ _

Сила упругости пружины К₂ равна силе PtzcosQz, приложенной к М, и направлена ей противоположно.

Практическое воплощение простейшего динамического поглотителя колебаний, или, как его называют, резонансного демпфера, покажем на следующем рисунке.

К вибрирующей поверхности жестко крепится упругий стержень, где находится масса, которую можно закрепить в любом положении по длине стержня. Ее перемещением добиваются, чтобы собственная частота системы стержень-масса была равна частоте возбуждающей силы, приложенной к объекту.

Колебательные системы с распределенными параметрами

К таким системам относятся стержни, мембраны, пластины (рис. 2.5). Уравнения колебаний таких систем подробно рассматривают в курсах по колебаниям панелей, оболочек.

Автоколебания

В рассмотренных системах колебания возникают под воздействием на них внешних возбуждающих сил и характер данных колебаний зависит от этих сил. Если сила гармоническая, то и колебания будут гармоническими.

Но имеются и другие системы, в которых колебания происходят с частотой собственных колебаний. В них колебательный процесс определяют не внешние воздействия на систему, а сама система. Колебания зарождаются внутри самой системы. Она сама генерирует колебания. Такие колебания называют автоколебаниями. Есть много примеров: струна, колеблющаяся при движении смычка, органная труба.

Источник