Компрессионное испытание грунта

Компрессионные испытания — наиболее распространенный вид лабораторных исследований для определения деформационных характеристик (свойств) грунтов. Компрессия — это процесс сжатия фунта без возможности бокового расширения (ε х =ε y =0), т.е. уплотнение образца без его разрушения.

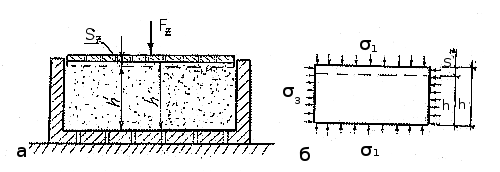
Компрессионные испытания грунтов в лабораторных условиях проводятся в компрессионных приборах (одометрах). Конструкции их бывают различные, в зависимости от способа приложения нафузки и целей исследования. В качестве примера на рис. 5.2 показан общий вид прибора для компрессионного испытания фунта.

На компрессионное сжатие ( рис. 5.3 ) образец грунта испытывается в металлическом кольце, и на него через жесткий штамп передается сила F, вызывающая в образце сжимающее напряжение σ = F/A, где А — площадь поперечного сечения образца. Таким образом, под действием вертикальной нагрузки происходит вертикальное перемещение штампа, вызывающее осадку образца.

Рис. 5.2 Общий вид прибора для испытания грунта на компрессию

Рис. 5.3 Схема компрессионного испытания образца грунта

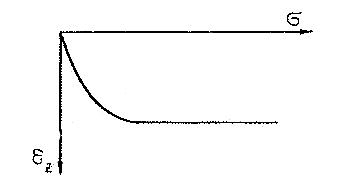
График зависимости относительных деформаций (ε z ) от сжимающих напряжений при компрессионном испытании показан на рис. 5.4:
(см. рис. 5.3).

Рис. 5.4. График зависимости ε z =ƒ(σ)

При испытании грунта на компрессию предварительно определяют плотность грунта р, плотность частиц грунта ps и природную влажность со грунта, по которым вычисляют начальный (до сжатия) коэффициент пористости грунта:

(5.2)

(5.3)

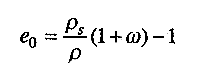
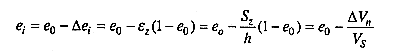
где ∆e i — изменение коэффициента пористости;
ΔV n — изменение объема пор образца грунта;
V s — объем твердых частиц грунта.

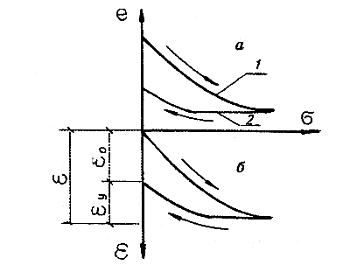
По значениям е, для различных напряжений строим кривую e=ƒ(P), которую назьгвают компрессионной кривой. На рис. 5.5 показаны компрессионные кривые для грунтов, не обладающих структурной прочностью.

Рис. 5.5. Компрессионные кривые (а) и зависимости изменения относительных деформаций от напряжений (б): 1 — кривая компрессии (уплотнения); 2 — кривая декомпрессии (набухания); ε 0 — относительная пластическая деформация; ε y — то же, упругая

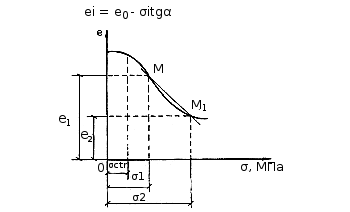
Для оценки сжимаемости грунтов в диапазоне реальных (строительных) нагрузок компрессионную кривую можно заменить прямой линией ММ1 ( рис. 5.6 ). Уравнение этой приямой

Рис. 5.6. Расчетная схема для определения коэффициента уплотнения (сжимаемости)

(5.5.)

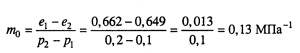
Коэффициент сжимаемости — расчетная характеристика деформируемости фунтов, которая используется при определении осадок сооружений. С помощью этого коэффициента можно производить качественную оценку грунта как основания зданий и сооружений:

(5.6)

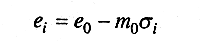
Продифференцировав это выражение, получим

(5.7)

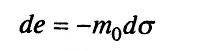
и тогда можно сформулировать закон уплотнения (компрессии): изменение коэффициента пористости грунта прямо пропорционально изменению давления.

Источник

Анализ компрессионной кривой

Как видно на рис. VIII-19 каждая компрессионная кривая может иметь две ветви — кривую уплотнения и кривую набухания Кривая уплотнения показывает уменьшение коэффициента пористости с увеличением давления, а кривая набухания — его увеличение после уменьшения давления. При последовательном уплотнении породы, разгрузке и повторном уплотнении кривые уплотнения и набухания образуют петлю гистерезиса (рис. VIII-21). При этом коэффициент пористости породы после снятия нагрузки в большинстве случаев не достигает того значения, которое он имел в начале опыта. Это объясняется образованием остаточных деформаций, которые проявляются в породах. Полная деформация породы под нагрузкой S складывается из необратимой S1 и обратимой S2.
Необратимые (остаточные) деформации возникают вследствие уменьшения пористости и увеличения плотности сложения породы в результате нарушения структурных связей и перемещения частиц и их агрегатов друг относительно друга Такие деформации называют структурными. В рыхлых несвязных песчаных и других обломочных породах структурные деформации протекают быстро, почти мгновенно. В глинистых породах они протекают не мгновенно, а с последействием, для их завершения требуется определенное время.

Обратимые деформации являются следствием сил упругости минеральных частиц, водных и коллоидных пленок, облекающих минеральные частицы, а также замкнутых пузырьков воды, воздуха или газов. Истинно упругие деформации протекают мгновенно и при давлениях, которые испытывают песчаные и глинистые породы от действия сооружений, ничтожны. Другая часть обратимых (восстанавливающихся) деформаций связана с изменением толщины гидратных оболочек, характерных для глинистых пород. При сближении частиц в таких породах, когда уплотняющее давление превышает силы расклинивающего давления пленок воды, т. е. когда внешнее давление превышает сорбционные силы взаимодействия породы с водой, толщина гидратных оболочек уменьшается. Косвенным показателем этого является изменение влажности породы.

При разгрузке породы или свободном доступе к ней воды (увлажнении) сорбционные силы могут превысить напряжения в ее структурных связях, толщина гидратных оболочек будет увеличиваться, а это вызовет разуплотнение и набухание породы. В некоторых типах глинистых пород такие деформации могут достигать больших размеров, особенно если первоначально устранить силы, сдерживающие набухание (нарушить структурные связи, снять внешнее давление). Поэтому коэффициент пористости породы после снятия давления может оказаться большим, чем в начале опыта. У таких разгруженных пород уплотнение часто происходит не за счет изменения естественной пористости, а вследствие того, что они были предварительно разуплотнены.

Обратимые деформации, связанные с изменением толщины гидратных оболочек, по предложению Н.Я. Денисова, принято называть структурно-адсорбционными. По перемещению частиц эти деформации сходны со структурными, но по значительной роли адсорбционных явлений они отличаются от них.

Структурно-адсорбционные деформации развиваются медленно, с последействием, для их завершения необходимо продолжительное время. Медленные структурно-адсорбционные деформации, развивающиеся под действием постоянного внешнего давления, называются ползучестью.

При уплотнении песчаных и других обломочных пород развиваются главным образом необратимые деформации, структурные, а упругие имеют подчиненное значение. При уплотнении глинистых пород происходят одновременно и обратимые, и необратимые деформации — упругие, структурные и структурноадсорбционные (табл. VIII-21).
При неоднократном уплотнении и разуплотнении породы общая деформация постепенно увеличивается, так как каждое повторное давление, особенно если оно больше предыдущего, вызывает дополнительную деформацию AS. На кривой сжатия образуется перелом. Этот перелом, очевидно, свидетельствует о том наибольшем напряжении, которое порода испытала ранее. Перелом на кривой уплотнения образуется часто и при первом цикле загрузки породы в компрессионном приборе, если первую ступень нагрузки прикладывать небольшими долями, например по 0,01 МПа, до того момента, пока не будет зафиксирована первая деформация породы. Это давление является эффективным, так как оно необходимо для начала сжатия и уплотнения породы, для преодоления или уравновешивания внутренних напряжений в породе (сорбционных сил — сил набухания) или прочности структурных связей. Если внешнее давление будет меньше эффективного (прочности структурных связей), деформация породы будет настолько мала, что ею можно пренебречь и рассматривать породу как квазитвердое тело.
На рис. VIII-22 видно, что разные породы имеют неодинаковую прочность структурных связей и соответственно для них неодинаково эффективное давление. Чем древнее порода, тем больше эффективное давление и тем меньше ее сжимаемость при давлении выше эффективного. Так, например, у поздне- и послеледниковых глинистых пород она составляет 0,03—0,05 МПа, у моренных ледниковых — 0,1, у каменноугольных и девонских соответственно 0,1 и 0,2, у кембрийских синих глии — 0,4—0,5, а у верхнепротерозойских превышает 0,6.

На рис. VIII-24 показано влияние предварительного набухания глин, а на рис. VIII-25 — их набухание после уплотнения нагрузками до 1,5 МПа. В первом случае структурные связи в породе были нарушены расклинивающим давлением пленок воды, проникающей в породу, а во втором — действием нагрузки. На рис. VIII-24 видно, что значительная часть сжатия глин произошла в результате их предварительного разуплотнения (набухания) при свободном доступе влаги. Рис. VIII-25 показывает, что набухание глин после уплотнения происходит быстро и достигает сравнительно значительных размеров; если после такого набухания их вновь начать уплотнять, то, естественно, значительная сжимаемость их будет также результатом только разуплотнения и набухания.
На рис. VIII-26 и VIII-27 показаны результаты испытания глин на сжатие при естественной влажности. Причем как в том, так и в другом случае при давлении выше эффективного (1,6 и 1,4 МПа) глины трижды уплотнялись до 2,0 МПа и 2 раза разуплотнялись до эффективного давления, а третий раз — до нуля, т. е. выше эффективного давления получены петли гистерезиса. Из этих кривых видно, что рассматриваемые глинистые породы слабосжимаемы, обладают малыми остаточными деформациями, в них проявляются главным образом упругие деформации.
На рис. VIII-28 приведены типичные компрессионные кривые послеледниковых иольдиевых глин из долины р. Кемь (Карелия). На этих кривых видно, что коэффициент пористости глин при давлении, равном нулю, соответствующий естественным условиям залегания, необычно велик. Эффективное давление для этих пород мало, оно составляет 0,02—0,05 МПа, при превышении его глины начинают сильно уплотняться. При нарушении естественного сложения сжимаемость их резко увеличивается во много раз начиная с малых давлений. При разгрузке глин после уплотнения обнаруживаются большие остаточные деформации, которые, несомненно, являются следствием главным образом структурных деформаций.
На рис. VIII-29 приведены компрессионные кривые мелкозернистого песка рыхлого сложения и песка, уплотненного трамбованием. Песок рыхлого сложения значительно сжимаем и имеет большие остаточные деформации явно структурного характера. У песка плотного сложения сжимаемость значительно меньше, а остаточные деформации невелики. Все это показывает, что на деформируемость песчаных и вообще обломочных пород большое влияние оказывает плотность сложения.

Источник

Компрессионная зависимость.

Уплотнение грунта сплошной постоянной нагрузкой называется компрессией грунтов (Рис. 3.1.). При этом деформации грунта могут развиваться только в одном направлении и никакие силы, кроме внешней нагрузки, не действуют (одномерная задача).

Для испытания грунта на сжимаемость применяют приборы с жёсткими стенками (одометры) для обеспечения сжатия грунта только в одном направлении (без возможности его бокового расширения). Компрессионное сжатие грунта оценивается изменением коэффициента пористости при изменении сжимающих напряжений в скелете грунта. Поскольку образец грунта в кольце не может получить бокового расширения, изменение его коэффициента пористости e_i под давлением p_i, распределённым по площади A, найдём по выражению:

, (3.1)

(3.2)

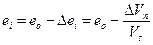
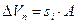
Объём твёрдых частиц в единице объёма образца грунта m остаётся практически неизменным и составляет 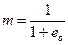. (3.3)

Тогда 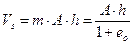. (3.4)

Подставляя уравнения (3.2) и (3.4) в уравнение (3.1), получим выражение:

. (3.5)

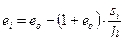
Эта формула позволяет определять коэффициент пористости грунта для любого приложенного давления. По значениям e_i для различных давлений p_i можно построить кривую зависимости коэффициента пористости от давлений, которую называют компрессионной кривой.

Закономерность изменения коэффициента пористости, установленная К. Терцаги, развита многими отечественными учёными (Н.М. Герсевановым, Н.А. Цытовичем, Н.Н. Масловым, М.Н. Гольдштейном и др.).

Рис. 3.3. Компрессионные кривые.

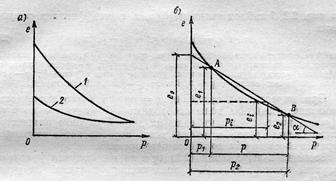
а) общая закономерность:

б) расчётная схема для определения коэффициента относительной сжимаемости.

Источник

Основная зависимость компрессионных свойств рыхлых несвязных и мягких связных горных пород. Компрессионная кривая

На компрессионные свойства песчаных и глинистых пород влияют многие факторы. Это влияние в большинстве случаев может быть охарактеризовано только качественно. Количественно оно лучше всего определяется зависимостью изменения пористости пород от действующего внешнего давления. Поэтому для оценки сжимаемости (деформируемости) песчаных и глинистых пород принято исследовать влияние внешнего давления на изменение их пористости или коэффициента пористости.
Эта зависимость весьма характерна и выражается обычно в виде компрессионной кривой (рис. VIII-19), из которой видно, что определенному давлению о1 соответствует определенный коэффициент пористости породы е1. При увеличении давления до о2 соответственно уменьшается коэффициент пористости породы до е2. Если изменение давления будет мало, т. е. о2—о1=dщ, то и коэффициент пористости изменится мало, т. е. е1—e2=de. На малом участке компрессионной кривой от М1 до М2 ее можно считать прямой. Тангенс угла наклона этого участка кривой характеризует сжимаемость породы на данном интервале давления
Чем больше tgа, тем порода слабее, так как она более податлива, сильнее уплотняется в пределах заданного интервала давлений. Тангенс угла наклона компрессионной кривой, т. е. tga, принято обозначать через а и называть коэффициентом сжимаемости. Следовательно, это угловой коэффициент, выражающий зависимость пористости от давления. Так как е есть отвлеченное число, а с измеряется в паскалях или мегапаскалях, то а соответствует 1/10в5 Па, или 1/0,1 МПа. Приближенно можно считать, что при небольших нагрузках (0,05—0,5 МПа) на песчаные и глинистые породы, если а=1/0,1 МПа, они являются чрезмерно сильносжимаемыми и сильносжимаемыми; если а составляет сотые доли этого значения — среднесжимаемыми, а если а выражается тысячными долями — слабосжимаемыми.

Из вышеприведенного равенства следует

Это уравнение выражает один из основных законов механики песчаных и глинистых горных пород — закон уплотнения. Формулируется он так: «Относительное изменение объема пор породы прямо пропорционально изменению давления». Этот закон выражает зависимость между коэффициентом пористости породы и внешним давлением и считается справедливым в определенных условиях для различных песчаных и других обломочных и глинистых пород. Интересно отметить, что основной закон механических свойств горных пород — закон уплотнения — аналогичен закону упругости в теории сопротивления материалов. Действительно, согласно закону Гука имеем

где относительная деформация X прямо пропорциональна напряжению о.

Сравнивая уравнения, выражающие закон уплотнения и закон упругости, видим, что коэффициент пористости породы е аналогичен значению относительной деформации Л, а коэффициент сжимаемости а аналогичен обратному значению модуля нормальной упругости Е.

На рис. VIII-20, а видим, что каждый элементарный объем породы в основании фундаментов сооружений находится в состоянии пространственного объемного напряжения — трехосного сжатия. Под воздействием этого сжатия, обусловленного весом сооружения и вышележащих толщ горных пород, породы основания деформируются.
Многочисленными исследованиями установлено, что между деформациями и напряжениями существует зависимость X=f(a). Типичный характер этой зависимости показан на рис. VIII-20, б, из которого видно, что в пределах определенного интервала нагрузок (обычно до 0,5—0,6 МПа) с достаточной для практических целей точностью можно считать ее линейной, а породы в этих пределах нагрузок — линейно деформируемыми телами. Эта зависимость справедлива для самых различных песчаных и глинистых пород и выражает важнейшую общую закономерность их механических свойств — закон деформируемости. Он позволяет в практике инженерных расчетов применять теорию упругости и для песчаных, и для глинистых пород.

Исследования показывают, что глинистые породы в природных условиях в некоторых случаях не подчиняются закону уплотнения и при одинаковом давлении могут обладать различной плотностью. Это объясняется тем, что определенная пористость породы в некоторых случаях обусловлена не только воздействием определенного давления. Сжатие осадка в процессе его накопления и при последующей литификации происходит под влиянием силы тяжести, преодолевающей силы трения и сцепления между минеральными частицами. При этом эффект уплотнения при одинаковом давлении будет различен в зависимости от пористости и влажности породы, от минерального состава частиц, ее слагающих, от степени «глинистости», характера и прочности возникающих структурных связей, ее цементации и др.

Так как коэффициент сжимаемости

Раскрывая скобки и группируя члены, будем иметь

Обозначая эту постоянную величину через А, получим уравнение, связывающее пористость породы с давлением:

Если в этом выражении о = 0, то постоянная величина А будет равна коэффициенту пористости породы при давлении, равном нулю, т. е. А = е0. На рис. VIII-19 величина А представлена как начальный параметр компрессионной кривой, получаемый продолжением прямой M1M2 до пересечения с осью ординат.

Выбор точек M1 и M2 на компрессионной кривой при определении коэффициента сжимаемости а не может быть случайным, а должен быть подчинен определенному правилу. Координаты точки M1 должны соответствовать естественному природному давлению на породу o1 и естественному коэффициенту пористости e1. Координаты точки M2 должны соответствовать конечному давлению на породу о2 после возведения сооружения. По конечному давлению о2 на компрессионной кривой находят значение е2.

При определении конечного давления необходимо иметь в виду, что оно должно удовлетворять следующему равенству:

где g — давление от проектируемого сооружения, МПа; h — глубина заложения подошвы фундамента сооружения, см; у — плотность породы, залегающей выше подошвы фундамента сооружения, г/см3. Величина g—hy означает давление на породу от сооружения за вычетом веса породы, т. е. фактически то дополнительное давление, которое порода воспримет после возведения сооружения.

Мерой компрессионной способности породы может быть также коэффициент относительной сжимаемости а0, выражающий относительную деформацию породы, т.е. представляющий сжатие слоя породы от давления о (МПа), отнесенное к первоначальной мощности слоя. Часто коэффициент относительной сжимаемости определяют как сжатие слоя породы мощностью в 1 м под давлением ст (МПа). Этот показатель выражают в процентах или в миллиметрах на метр (осадка в миллиметрах слоя породы мощностью в 1 м).

Коэффициент относительной сжимаемости может быть вычислен по следующей формуле

где а0 — коэффициент относительной сжимаемости, %, Ah — изменение высоты образца породы при полной стабилизации ее уплотнения от данного давления, h — первоначальная высота испытуемого образца породы.

Для теоретических построений иногда необходимо выражать компрессионную кривую аналитически. Как указывал И.M. Герсеванов на основании большого числа экспериментов, проведенных разными исследователями над песчаными и глинистыми породами, эти кривые выражаются формулой
где о1 = 0,1 МПа, а величины е1, А и С являются параметрами кривой. Величина С в этой формуле, как показали опыты, очень мала по сравнению с о1, а потому обычно пользуются формулой
В таком виде эта формула отражает довольно точно очертание компрессионной кривой для всех значений о начиная от о1 = 0,1 МПа. Меньшие давления практического значения для строительства не имеют. Точно такого же вида формулой может быть выражена и кривая набухания, но, естественно, при других значениях параметров е1 и А.

При определении по компрессионной кривой (рис. VIII-19) ее параметров достаточно обратить внимание на то, что при e = e1 логарифм, стоящий в правой части уравнения, обращается в нуль, а следовательно, e1 есть ордината кривой, соответствующая давлению, равному 0,1 МПа. Если через e1 обозначить ординату кривой, соответствующую давлению о=0,272 МПa, то из вышеприведенного уравнения получим

При использовании выводов теории упругости и механики горных пород для учета и оценки их деформации кроме основных параметров компрессионной кривой — коэффициента сжимаемости а и величины А = е+ао — необходимо знать и некоторые другие характеристики.

Рассматривая горные породы как линейно деформируемые тела и учитывая, что в условиях естественного залегания (или в теле земляных сооружений) они находятся в условиях объемного трехосного сжатия, при исследовании их сжимаемости (деформируемости) к ним можно применить следующие зависимости между напряжениями oz, ox и oy и соответствующими им относительными деформациями еz, еx и ey из теории сопротивления материалов:
Параметры, входящие в эти уравнения,— модуль общей деформации E0 и коэффициент поперечной деформации (коэффициент Пуассона) u — являются количественными характеристиками механических свойств пород — их способности деформироваться при сжатии. Они считаются основными характеристиками пород при проектировании оснований зданий и сооружений и расчетах их осадок (СНиП II—15—74).

Модулем общей деформации называется коэффициент пропорциональности между напряжением и соответствующей ему относительной деформацией породы

Он равен отношению сжимающего напряжения oz к вызываемой им относительной деформации породы ez при сжатии в условиях без возможности бокового расширения породы

Модуль общей деформации выражают в мегапаскалях. Его определяют путем специальных полевых и лабораторных исследований или вычисляют по данным компрессионных испытаний по формуле
о1; a — коэффициент сжимаемости 1/0,1 МПа, определяемый по компрессионной кривой для интервала нагрузок от о1 до о2, в — множитель для перехода от сжатия без возможности бокового расширения при компрессионных испытаниях к сжатию, имеющему место в натуре. Численно он равен для песков — 0,76; для супесей — 0,72, для суглинков — 0,57, для глин — 0,43 Значение в определяется по коэффициенту поперечного расширения в или коэффициенту бокового давления е по одной из следующих формул
Модуль общей деформации есть характеристика, аналогичная модулю упругости твердых тел. Однако песчаные и глинистые породы в отличие от твердых тел обладают значительными остаточными деформациями, часто намного превышающими упругие. Поэтому модуль общей деформации этих пород в отличие от модуля упругости характеризует общие их деформации на сжатие, как упругие, так и остаточные. Следует заметить, что прямая пропорциональная зависимость между напряжениями и относительными деформациями у песчаных и глинистых пород устанавливается в пределах сравнительно ограниченного интервала давления (рис. VIII-20, б). Поэтому модуль общей деформации есть характеристика свойств рассматриваемых пород для этого ограниченного интервала давлений. Так как при проектировании и строительстве различных сооружений имеют дело с умеренными давлениями на песчаные и глинистые породы, последние можно рассматривать как среду, в которой вполне применим такой показатель свойств.
Таким образом, для песчаных и глинистых пород в определенных пределах напряжений характерна линейная зависимость между общей их деформацией и вызывающим ее напряжением. Эта зависимость является второй основной закономерностью их механических свойств (закон деформируемости). Ее можно сформулировать так относительная общая деформация песчаных и глинистых пород прямо пропорциональна действующим напряжениям. Вычисление модуля общей деформации производят для определенного интервала давлений. Средние его значения показаны в табл. VIII. 20.

Коэффициент поперечного расширения (коэффициент Пуассона) является коэффициентом пропорциональности между поперечными и продольными относительными деформациями. Он равен отношению относительного поперечного (горизонтального) расширения еу к относительному продольному (вертикальному) сжатию еz

Для песчаных и глинистых пород он изменяется от 0,2 до 0,5. Среднее его значение для различных типов пород по СНиП равно крупнообломочные породы — 0,27, пески и супеси — 0,30, суглинки — 0,35, глины — 0,42.

Этот коэффициент можно вычислять также и по формуле

где е — коэффициент бокового давления, показывающий, какая часть вертикального давления передается через породу в стороны. Численно он равен отношению бокового давления породы Pб к вызвавшему его вертикальному давлению P

Коэффициент бокового давления изменяется в пределах от 0 до 1. По данным опытных работ различных авторов он равен для песков — 0,35—0,41, для суглинков — 0,50—0,70, для глин — 0,20—0,74. Определяется он в приборах особой конструкции или вычисляется по формуле

Источник