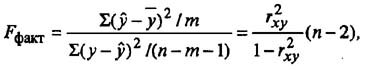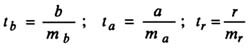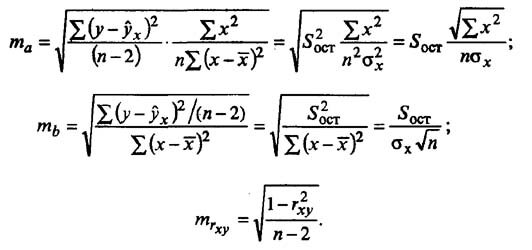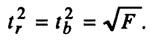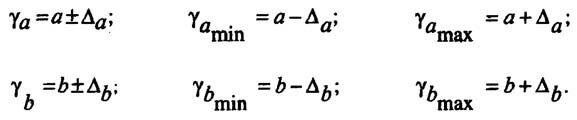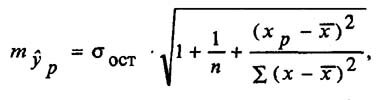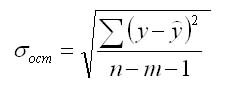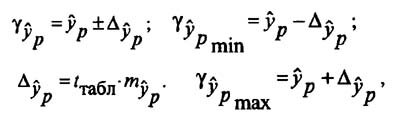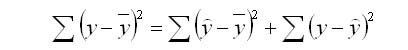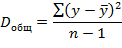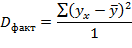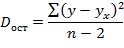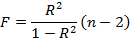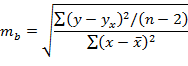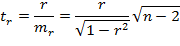Критерий фишера применяется для определения качества оценок параметров уравнения регрессии
Проверка качества уравнения регрессии. F-критерий Фишера. t-критерий Стьюдента.



После того как уравнение регрессии найдено, проводится оценка значимости как уравнения в целом, так и его отдельных параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Согласно F-критерию Фишера, выдвигается «нулевая» гипотеза H0 о статистической незначимости уравнения регрессии и показателя тесноты связи.
Непосредственному расчету F-критерия предшествует анализ дисперсии.
Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и εi:
Из данного уравнения следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е) (остаточной дисперсией Dост = D(ε)):


| полная (общая) сумма квадратов отклонений | = | сумма квадратов отклонений, объясненная регрессией | + | (остаточная) сумма квадратов отклонений, не объясненная регрессией |
где m – число независимых переменных в уравнении регрессии (для парной регрессии m = 1);
n– число единиц совокупности.
Если нулевая гипотезаН0 справедлива, то факторная и остаточная дисперсии не отличаются друг от друга (т. е. отличие величины F от нуля статистически незначимо).
Если нулевая гипотеза Н0не справедлива, то факторная дисперсия превышает остаточную в несколько раз.
Справедливость (несправедливость) гипотезы Н0 определяется по таблицам критических значений F-критерия Фишера, которые разработаны английским статистиком Снедекором для разных уровнях значимости нулевой гипотезы и различного числа степеней свободы.
Уровнем значимости (обозначается α) в статистических гипотезах называется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.
Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы.
Если Fфакт >Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения.
Если Fфакт
Стандартные ошибки параметров регрессии (ma, mb) определяются соотношениями:
Сопоставляя оценки параметров и их стандартные ошибки можно сделать вывод о надежности (точности) полученных оценок.
Для оценки статистической значимости коэффициентов регрессии применяется t-критерий Стьюдента, согласно которому выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или b от нуля):
t-критерий Стьюдента используется и для оценки статистической значимости выборочного коэффициента корреляции rxy:
Оценка значимости параметров уравнения и коэффициента корреляции проводится путем сопоставления их значений с величиной случайной ошибки:
Если tфакт >tтабл, то Н0 отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.
Если tфакт
Под доверительным интервалом понимаются пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью (P = 1-α).
Доверительные интервалы для параметров a и b уравнения линейной регрессии определяются соотношениями:


Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается равным нулю, так как он не может одновременно принимать и положительное, и отрицательное значения.
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
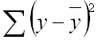
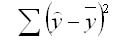
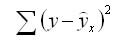
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Использование критерия Фишера для проверки значимости регрессионной модели
Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:
Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f1 равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f1=1). Число степеней свободы необъясненной дисперсии f2 = N–k-1, где N-количество экспериментальных точек, k-количество объясняющих переменных (например, для модели Y=A*X+B подставляем k=1).
Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным, взятым для числа степеней свободы f1 (бóльшая дисперсия) и f2 (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.
Коэффициент корреляции и F-критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих метод наименьших квадратов.
Оценка значимости по критериям Фишера и Стьюдента
После выбора уравнения линейной регрессии и оценки его параметров проводится оценка статистической значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера, который называют также F-критерием. При этом выдвигается нулевая гипотеза (Н0): коэффициент регрессии равен нулю (b = 0), следовательно, фактор х не оказывает влияния на результат у и линия регрессии параллельна оси абсцисс.
Перед тем как приступить к расчету критерия Фишера, проведем анализ дисперсии. Общую сумму квадратов отклонений у от 
Общая сумма квадратов отклонений результативного признака у от среднего значения 

Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов:
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс, обусловленный как влиянием фактора х, (регрессией у по х), так и действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации R 2 будет приближаться к единице.
Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с числом свободы независимого варьирования признака.
Существует равенство между числами степеней свободы общей, факторной и остаточной сумм квадратов.Запишем два равенства:
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим дисперсии на одну степень свободы:
Так как эти дисперсии рассчитаны на одну степень свободы, их можно сравнивать между собой. Критерий Фишера позволяет проверить нулевую гипотезу Н0 о том, что факторная и остаточная дисперсии на одну степень свободы равны между собой (Dфакт=Dост). Критерий Фишера рассчитывается по следующей формуле:
Если гипотеза Н0 подтверждается, то факторная и остаточная дисперсии одинаковы, и уравнение регрессии незначимо. Чтобы отвергнуть нулевую гипотезу и подтвердить значимость уравнения регрессии в целом, факторная дисперсия на одну степень свободы должна превышать остаточную дисперсию на одну степень свободы в несколько раз. Существуют специальные таблицы критических значений Фишера при различных уровнях надежности и степенях свободы. В них содержатся максимальные значения отношений дисперсий, при которых нулевая гипотеза подтверждается. Значение критерия Фишера для конкретного случая сравнивается с табличным, и на основе этого гипотеза Н0 принимается или отвергается.
Между критерием Фишера и коэффициентом детерминации существует связь, которая выражается следующей формулой для парной линейной регрессии:
В линейной регрессии часто оценивается не только значимость уравнения регрессии в целом, но и значимость его отдельных параметров, а также коэффициента корреляции.
Теперь нужно рассчитать критерии Стьюдента ta, tb, tr·. Для параметров а, b и коэффициента корреляции r критерий Стьюдента определяет соотношение между самим параметром и его ошибкой:
Фактические значения критерия Стьюдента сравниваются с табличными при определенном уровне надежности α и числе степеней свободы df= (п-2). По результатам этого сравнения принимаются или отвергаются нулевые гипотезы о несущественности параметров или коэффициента корреляции. Если фактическое значение критерия Стьюдента по модулю больше табличного, тогда гипотеза о несущественности отвергается. Подтверждение существенности коэффициента регрессии равнозначно подтверждению существенности уравнения регрессии в целом.
В парной линейной регрессии между критерием Фишера, критериями Стьюдента коэффициентов регрессии и корреляции существует связь.
На основании полученной связи можно сделать вывод, что статистическая незначимость коэффициента регрессии или коэффициента корреляции влечет за собой незначимость уравнения регрессии в целом, либо, наоборот, незначимость уравнения регрессии подразумевает несущественность указанных коэффициентов.
На основе стандартных ошибок параметров и табличных значений критерия Стьюдента можно рассчитать доверительные интервалы:
Дата добавления: 2015-10-05 ; просмотров: 13085 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Проверка качества уравнения регрессии. F-критерий Фишера
Оценка качества полученного уравнения регрессии основывается на мето-дах дисперсионного анализа.
Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и еi
Величина ŷi=а+ b·хi представляет собой расчетное значение переменной у в наблюдении i. Остаток еi есть расхождение между наблюдаемым и расчетны-ми значениями переменной у, или необъясненная с помощью уравнения рег-рессии часть переменной у.
Из (2.21) следует следующее соотношение между дисперсиями наблюдае-мых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е)
называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи.
Соотношение (2.23) можно представить в альтернативном виде
| n | ||||
| Dост | R 2 1 | ( yˆiyi ) 2 | ||
| R 2 1 | или | i 1 | . | (2.25) |
| D( y) | n | |||
| ( yi |
Коэффициент детерминации R 2 принимает значения в диапазоне от нуля до
Коэффициент детерминации R 2 показывает, какая часть дисперсии резуль-тативного признака y объяснена уравнением регрессии. Например, значение R 2 = 0,56говорит о том,что соответствующее уравнение регрессии объясняет56 % дисперсии результативного признака.
Возникает вопрос, при каких значениях R 2 уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использо-вание в анализе. Ответ на этот вопрос дает F-критерий Фишера.
Введем следующие обозначения:
| n | |||
| TSS = ( yi | полная сумма квадратов отклонений; | ||
| i 1 | |||
| n | |||
| ESS = ( yˆi | объясненная сумма квадратов отклонений; | ||
| i 1 | |||
| n | n | ||
| RSS = ( yˆiyi ) | 2 ei | необъясненная сумма квадратов отклонений. | |
| i 1 | i 1 | ||
| Известно, что величина | ESS | ||
| F | k | , | (2.26) |
| RSS |

где k число независимых переменных в уравнении регрессии (для парной рег-рессии k= 1), в случае нормально распределенной ошибки εi является F-статис-тикой Фишера (случайная величина, распределенная по закону Фишера) с чис-лом степеней свободы k1=k,k2=n k1.
Согласно F-критерию Фишера, выдвигается « нулевая» гипотеза H0 о ста-тистической незначимости уравнения регрессии (т. е. о статистически незначи-мом отличии величины F от нуля). Эта гипотеза отвергается при выполнении условия F>Fкрит, где Fкрит определяется по таблицам F-критерия Фишера (П3,
П4) при числе степеней свободы k1=k, k2=n k1 и заданному уровню зна-чимости α.
Уровнем значимости (обозначаетсяα)в статистических гипотезах называ-ется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.
Используя соотношение (2.24), величину F можно выразить через коэффи-циент детерминации R 2
| F | R 2 | n k 1 | . | (2.27) |
| R 2 | k |
Например, по данным 30 наблюдений было получено уравнение регрессии y = 50,5 + 3,2x и R 2 = 0,60.
Необходимо проверить его значимость при уровне значимости α = 0,05. Определим величину F-статистики, учитывая, что k= 1
| F | R 2 | n k 1 | 0,6 | 30 | 1 1 | 0,6 | 42. |
| R 2 | k | 0,6 | 0,4 |
По таблицам F-критерия Фишера при