Легкие задачи с параметром

Что такое параметр? Простые задачи с параметрами

Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?

Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».

Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.

Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?

Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.

Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».

Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.

1. Теперь пример из школьной математики.

Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.

Дискриминант квадратного уравнения:

Если , квадратное уравнение имеет два корня: и

Если , то есть с > 1, корней нет.

В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.

Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.

И еще две простые задачи с параметром.

2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.

Квадратное уравнение имеет два различных корня, когда .

Найдем дискриминант уравнения

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).

Разложим левую часть неравенства на множители:

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

3. При каких значениях параметра k система уравнений не имеет решений?

Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:

Источник

Графический метод решения задач с параметрами

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

В первом уравнении выделим полный квадрат:

Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

2. Найдите все значения a, при которых уравнение имеет единственное решение.

Уравнение равносильно системе:

Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

Приводим подобные слагаемые в уравнении.

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

Решим систему графически:

Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением

Пусть С — точка касания.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

Решая это уравнение, получаем, что

3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

Второе уравнение при задает окружность с центром в точке и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),

В — точка касания окружности и окружности

длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:

Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.

Аналогично, для точки D:

и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.

4. При каких значениях a система уравнений имеет 4 решения?

И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

Просто выделили полный квадрат во втором уравнении.

Сделаем замену Система примет вид:

Вот теперь все видно! Рисовать будем в координатах

Графиком первого уравнения является ромб, проходящий через точки с координатами и

Графиком второго уравнения является окружность с радиусом и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда

2) Есть второй случай, и мы его найдем.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

Значит, Объединим случаи и запишем ответ:

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Источник

Урок по теме «Методы решения задач с параметрами»

Разделы: Математика

Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.

Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Пример 1. Найдите все значения параметра a, при которых уравнение:

(2a – 1)x 2 + ax + (2a – 3) =0 имеет не более одного корня.

При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.

Чтобы записать окончательный ответ, необходимо понять,

2. Графический метод.

В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).

Пример 2. Для каждого значения параметра a определите количество решений уравнения .

Заметим, что количество решений уравнения равно количеству точек пересечения графиков функций и y = a.

График функции показан на рис.1.

y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a 25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

1) Если а = 0, то уравнение имеет единственное решение t = 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.

Задача № 1. При каких значениях параметра b уравнение не имеет корней?

Задача №2. Найти все значения параметра a, при которых множество решений неравенства:

содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

Преобразуем обе части неравенства.

Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:

Рис.4

При a > 6 множество решений неравенства: .

Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).

Это

Задача № 3. В области определения функции взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.

1) Графиком дробно-линейной функции является гипербола. По условию x > 0. При неограниченном возрастании х дробь монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.

2) По определению степени область определения D(y) состоит из решений неравенства . При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.

Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.

Источник

Задача 18: уравнения и неравенства с параметром

Существует ровно три генеральных метода решения задач 18:

Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.

Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)

Глава 1. Графический подход § 1. Вебинар по задачам 18: модуль и окружности § 2. Как решать задачу 18: графический подход § 3. Задача 18: две окружности и модуль § 4. Задача 18: пересечение графиков окружности и модуля § 5. Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром. Глава 2. Аналитический подход § 1. Задачи 18: Аналитическое решение § 2. Окружность и модуль: задачи 18 с двумя параметрами § 3. Аналитическое решение задачи 18 с перебором различных вариантов Глава 3. Нестандартные приемы § 1. Задача 18: метод симметричных корней § 2. Как увидеть симметрию корней в задаче 18? § 3. Метод мажорант в задаче 18 § 4. Графическое решение сложных задач 18 с модулем § 5. Задание 18: Симметрия корней в системе уравнений § 6. Анализ знаков квадратного трёхчлена в сложных задачах 18 § 7. Применение производной для отыскания точек пересечения графиков § 8. Продвинутый метод симметричных корней § 9. Новая задача 18 с графическим решением

Источник

Задачи с параметром (страница 4)

Решите при всех значениях параметра \(a\) уравнение \[|2ax-4|=a\]

При \(a уравнение не имеет решений, так как левая часть неотрицательна. При \(a=0\) уравнение равносильно \(2\cdot 0\cdot x-4=0 \ \Rightarrow \ 0=4\) и также не имеет решений.
При \(a>0\) уравнение равносильно \[\left[\begin\begin &2ax-4=a\\ &2ax-4=-a \end\end\right. \quad\Rightarrow\quad \left[\begin\begin &x=\dfrac<4+a><2a>\\[2ex] &x=\dfrac<4-a> <2a>\end\end\right.\] следовательно, имеет два различных корня.

\(a\leqslant 0 \ \Rightarrow \ x\in\varnothing\) ;

Решите уравнение при всех значениях параметра \(a\) : \[(a^2+a)x-2a^2=3a\]

\(a=0 \ \Rightarrow \ x\in \mathbb\) ;

\(a=-1 \ \Rightarrow \ x\in \varnothing\) ;

Решите уравнение при всех значениях параметра \(a\) : \[\dfrac=0\]

\(a=1 \ \Rightarrow \ x\in \varnothing\) ;

\(a\ne 1 \ \Rightarrow \ x=a\)

Найти, при каких значениях параметра \(a\) уравнение \[\sqrt\cdot (a(x^2+1)+a^2x+x)=0\]

имеет единственное решение.

Тогда исходное уравнение равносильно системе: \[\begin x\geqslant a\\ \left[ \begin \begin &x+a=0 \\ &ax+1=0 \qquad (*)\\ &x-a=0 \end \end \right. \end\]

Рассмотрим два случая:

\[\sqrt[3]+4\sqrt[3]=5\sqrt[3] <-x^2>\quad \Rightarrow \quad 10\sqrt[3]=0 \quad \Rightarrow \quad x=0\]

является луч (может быть, открытый).

Данное неравенство равносильно:

\(\log_(a^2x(x-1))>\log_(x^2-3x+2) \Rightarrow\quad \) по методу рационализации:

\[\begin x^2-3x+2>0\\ x^2-3x+2\ne 1\\ a^2x(x-1)>0\\ (x^2-3x+2-1)(a^2x(x-1)-x^2+3x-2)>0 \end \Rightarrow\]

\[\begin x\in(-\infty;1)\cup(2;+\infty)\\ x\ne \dfrac<3\pm \sqrt5>2\\ x\in (-\infty;0)\cup(1;+\infty)\\ a\ne 0\\ (x^2-3x+1)((a^2-1)x^2-(a^2-3)x-2)>0 \end \Rightarrow\]

Значит, значения \(a=-1;1\) нам подходят.

Тогда выражение можно преобразовать:

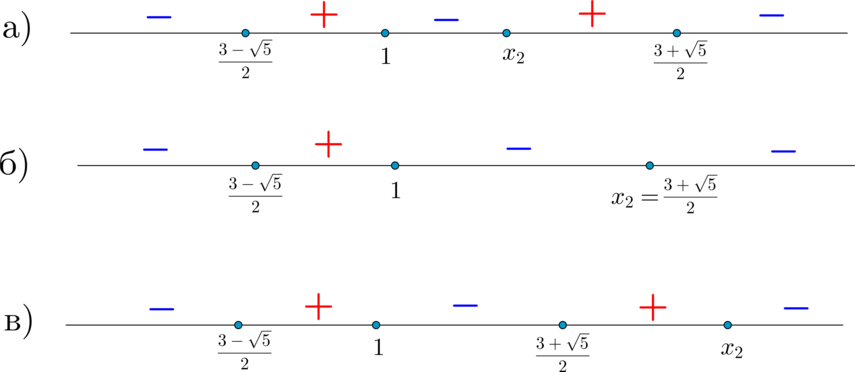
Таким образом, корень \(x_2\) может располагаться:

Посмотрим, как будет выглядеть метод интервалов в этих случаях:

Таким образом, в каждом из случаев а, б, в решение будет выглядеть как интервал или объединение двух интервалов, что после пересечения с ОДЗ не будет лучом. Следовательно, эти случаи нам не подходят.

Источник