Линейные системы с сосредоточенными параметрами

Для построения подобных моделей можно использовать два пути: применять фундаментальные физические соотношения и виде (дифференциальных) законов сохранения вещества, энергии и т. д. или восстанавливать параметры моделей по эмпирическим данным, причем второй путь чаще применяется на практике. Какие бы соображения ни использовались при построении моделей рассматриваемого класса, ими могут быть описаны многие реальные объекты управления.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

СИСТЕМЫ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

Смотреть что такое “СИСТЕМЫ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ” в других словарях:

СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ — (распределённые системы), системы, состоящие из элементов, непрерывно распределённых в конечных областях пр ва, так что происходящие в них движения передаются от одного элемента к другому и не могут быть идеализированы как движения объектов (масс … Физическая энциклопедия

Система с сосредоточенными параметрами — 71. Система с сосредоточенными параметрами Система, оператор которой может быть представлен в виде одного или системы обыкновенных дифференциальных уравнений Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и… … Словарь-справочник терминов нормативно-технической документации

ГОСТ 21878-76: Случайные процессы и динамические системы. Термины и определения — Терминология ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа: Cross power spectral density function of stationary dependent random processes Определения термина из разных документов: Cross power… … Словарь-справочник терминов нормативно-технической документации

СИСТЕМА С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ — (распределённая система) система, пространственные масштабы движения в к рой соразмерны с пространственнымимасштабами изменения физ. параметров. Термин «С. с р. п.» возник при становлениипроводной телеграфии для характеристики линии передач как… … Физическая энциклопедия

ЛИНЕЙНЫЕ СИСТЕМЫ — системы, (движения в к рых удовлетворяют суперпозиции принципу и описываются линейными ур ниями. Л. с. всегда явл. идеализацией реальной системы. Упрощения могут относиться как к параметрам, характеризующим систему, так и к движению в ней. Напр … Физическая энциклопедия

Устойчивость системы автоматического управления — Устойчивость системы автоматического управления, способность системы автоматического управления (САУ) нормально функционировать и противостоять различным неизбежным возмущениям (воздействиям). Состояние САУ называется устойчивым, если отклонение… … Большая советская энциклопедия

Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия

Электроакустические преобразователи — устройства, преобразующие электрическую энергию в акустическую (энергию упругих колебаний среды) и обратно. В зависимости от направления преобразования различают Э. п.: излучатели и приёмники. Э. п. широко используют для излучения и… … Большая советская энциклопедия

ЭЛЕКТРОАКУСТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ — устройство, преобразующее эл. магн. энергию в энергию упругих волн в среде и обратно. В зависимости от направления преобразования различают Э. п.: излучатели и приёмники. Э. п. широко используют для излучения и приёма звука в технике связи и… … Физическая энциклопедия

ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ — устройства, преобразующие эл. магн. энергию в энергию упругих волн в среде и обратно. В зависимости от направления преобразования различают Э … Физическая энциклопедия

Источник

Ширина спектра ЧМ-колебания с малым индексом модуля­ции равна 2Ω, т.е. определяется шириной спектра модулирующе­го сигнала. В случае большого индекса модуляции ширина спектра ЧМ-колебания равна 2∆ω и определяется девиацией частоты (4.15).

4.7. Фазовая модуляция

Фазомодулированный сигнал описывается выражением (4.10). Его мгновенная фаза согласно (4.9) определяется из выражения

(4.18)

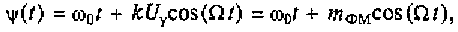
где m_фн = kU_y— коэффициент фазовой модуляции.

В соответствии с (4.18) мгновенная частота ФМ-сигнала

где ∆ω = kUyΩ — девиация частоты при фазовой модуляции.

ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ

ЛИНЕЙНЫЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

5.1. Классификация радиотехнических цепей

Радиотехническими цепями называют электрические цепи, при­меняемые в радиоэлектронных устройствах. Поэтому анализ ра­диотехнических цепей базируется на использовании общей тео­рии электрических цепей.

Радиотехнические цепи классифицируются по следующим при­знакам.

1. По числу внешних выводов (полюсов, портов) цепи, кото­рыми данная цепь соединяется с источниками сигналов, нагру­зочными элементами или другими электрическими цепями.

2. По наличию источника энергии внутри радиотехнической цепи (цепь активная, если имеется источник энергии, пассивная цепь — при его отсутствии).

3. По характеру процессов, протекающих в цепи, реакции (от­клику) цепи на внешнее воздействие. В линейной цепи (табл. 5.1) зависимость напряжения, тока или мощности отклика цепи от внешнего воздействия носит линейный характер. В нелинейной цепи (см. табл. 5.1) вольт-амперная характеристика (ВАХ) хотя бы од­ного элемента носит нелинейный характер. И, наконец, в пара­метрической цепи имеется хотя бы один элемент, у которого один или несколько параметров зависят от времени.

Графические обозначения элементов радиотехнических цепей

4. По сосредоточенным либо распределенным параметрам.

Под цепью с сосредоточенными параметрами понимают цепь, в которой выделяется конечное число элементов (участков) с гео­метрическими размерами, существенно меньшими длины элект­ромагнитной волны. К таким элементам цепи относят индуктив­ные катушки, конденсаторы, резисторы и т.д.

Цепи, в которых геометрические размеры элементов (участ­ков.) превышают длину электромагнитной волны, называются цепями с распределенными параметрами. К таким элементам цепи относят, например, волноводы и коаксиальные кабели.

Линейными называются цепи, состоящие только из линейных элементов, под которыми понимают элементы с параметрами, остающимися постоянными при приложении к ним напряжения и или тока i и не зависящими от их значений и направления. К ли­нейным элементам (двухполюсным) можно отнести резистор R, индуктивную катушку Lи конденсатор С.

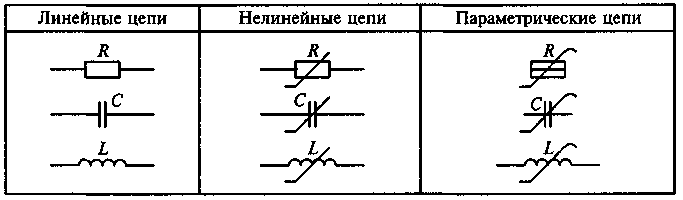
Так, для любой точки ВАХ резистора отношение напряжения к току u/i согласно закону Ома, равно сопротивлению Rэтого резистора и представляет собой постоянную величину. ВАХ по­добного резистора носит линейный характер. На рис 5.1 показан процесс формирования выходного тока в линейной цепи при воздействии гармонического сигнала. При приложении к этой цепи синусоидального напряжения с фиксированной частотой на вы­ходе цепи появится ток, имеющий вид гармонической функции той же частоты, что и напряжение.

Рис. 5.1. Процесс формирования выходного тока в линейной цепи

при воздействии гармонического сигнала

Для постоянного конденсатора линейный характер имеет кулон-вольтная характеристика, т.е. зависимость заряда, накапли­ваемого в конденсаторе, от напряжения, приложенного к нему. Для индуктивной катушки линейный характер носит вебер-амперная xарактеристика, т.е. зависимость заряда, накапливаемого в индуктивной катушке, от тока, протекающего через нее.

Отличительной чертой линейных цепей является то, что они под­чиняются принципу суперпозиции (наложения): при воздействии на цепь нескольких ЭДС любой формы и частоты отклики на каждую из ЭДС не зависят друг от друга. Полный отклик на выходе линейной цепи представляется суммой этих откликов. Например, так как со­противление линейной цепи не зависит от приложенного напря­жения, то любая вводимая в такую цепь ЭДС приведет к пропорцио­нальному приращению тока. Соответственно и результирующий ток в резисторе будет равен сумме токов, вызываемых отдельными ЭДС.

Нелинейными цепями называют такие цепи, в которые входят один или несколько нелинейных элементов, под которыми пони­мают элементы с параметрами, зависящими от напряжений и токов, приложенных к ним. Например, к числу нелинейных эле­ментов можно отнести полупроводниковый диод, ВАХ которого носит нелинейный характер. На рис. 5.2, а показаны графическое обозначение и ВАХ полупроводникового диода. Напряжение, при­ложенное к диоду, и ток, протекающий через него, связаны не­линейной зависимостью (рис. 5.2, б).

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Линейные системы с сосредоточенными параметрами

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

Классический метод расчета

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.

Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

;

при наличии магнитной связи с катушкой, обтекаемой током ,

;

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

.

(1)

Подставив в (1) значение тока через конденсатор

,

получим линейное дифференциальное уравнение второго порядка относительно

.

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:

,

(2)

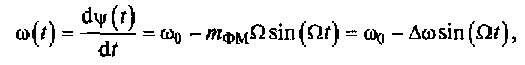
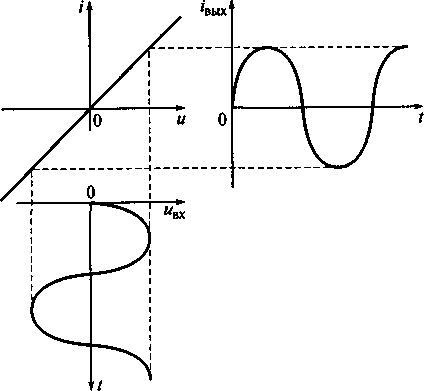
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); – известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); – к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

,

(3)

где и – соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; – число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); – число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная – свободной составляющей.

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид

(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Первый закон коммутации (закон сохранения потокосцепления)

Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Второй закон коммутации (закон сохранения заряда)

Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и , что приводит к нарушению законов Кирхгофа.

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:

первый закон коммутации – в ветви с катушкой индуктивности ток в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

второй закон коммутации – напряжение на конденсаторе в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .

Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.

В соответствии с законами коммутации

и .

На основании второго закона Кирхгофа для момента коммутации имеет место

,

и .

Для известных значений и из уравнения

определяется .

Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

.

Корни характеристического уравнения. Постоянная времени

Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).

Таблица 3. Выражения свободных составляющих общего решения

Вид корней характеристического уравнения

Выражение свободной составляющей

Корни вещественные и различные

Корни вещественные и

Пары комплексно-сопряженных корней

Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

,

которое называется декрементом колебания, или натуральным логарифмом этого отношения

,

называемым логарифмическим декрементом колебания, где .

,

где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при

Источник