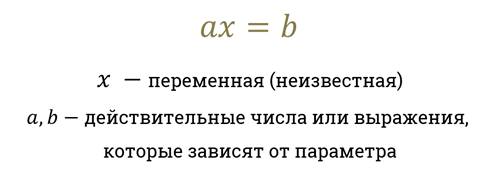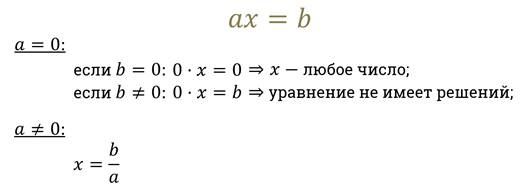Линейные уравнения с параметрами

Методическое пособие “Методы решения линейного уравнения с параметрами”

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Министерство обороны Российской Федерации

Федеральное государственное общеобразовательное учреждение

«Оренбургское президентское кадетское училище»

ЛИНЕЙНОГО УРАВНЕНИЯ С ПАРАМЕТРАМИ.

(Методические рекомендации для преподавателей и воспитанников)

Источник

Класс: 7

Презентация к уроку

Тип урока: введение нового материала.

Учебник: «Алгебра-7» авт. Ю.Н.Макарычев, Н.Г. Миндюк и др. издательство «Мнемозина», 2008 год.

I. Проверка домашнего задания (работа выполнялась на двойных листах и сдаётся на проверку).

Готовые решения проецируются на доску и разбирается (проговаривается) алгоритм решения.

№ 624. Решите уравнение:

а) 0,3(2x – 1) – 0,4 (x + 8) = 1,2x – 1;
0,6x – 0,3 – 0,4x – 3,2 = 1,2x – 1;
0,6x – 0,4x –1,2x = 0,3 + 3,2– 1;
– x = 2,5;
x = –2,5. Ответ: – 2,5.

в) – 6(2 – 0,2x) + 11 = – 4(3 – 0,3x) – 1;
– 12 + 1,2x + 11 = – 12 + 1,2x – 1;
1,2x – 1,2x = 12 – 11 + 1;
0x = 2. Ответ: решений нет.

№ 625. Решите уравнение

а) (2x – 1)(3x + 7) – (1 + 6x)(x + 2) = 4;
6x 2 + 14x – 3x – 7 – (x + 2 + 6×2 + 12x) = 4;
6x 2 + 14x – 3x – 7 – x – 2 – 6×2 – 12x = 4;
6x 2 + 14x – 3x – x – 6x 2 – 12x = 4 + 7 + 2;
– 2x = 13;
x = – 6,5. Ответ: – 6,5.

№ 626. Решите уравнение

№ 622. При каких значениях a уравнение ax = 2a – 1:

а) имеет единственный корень; (при a 0)
б) имеет бесконечно много корней; (таких значений a нет)
в) не имеет корней? (при a = 0).

II. Устная работа (задания проецируются на доску)

1. Найдите корни уравнения:

а) 14 + 3x = 5 – x ; (– 2,25)
б) 105y – 28 = 105y + 7;
в) 34x + 2 = 34x + 2. (x – любое число)

2. При каких значениях a число 3 является корнем уравнения?

3. Укажите контрольные значения, при которых уравнение не имеет решений или решением является любое число?

а) (5 – a) x = 0; б) (b + 4) x = 5; в) ax = x.

III. Изучение нового материала

Учитель. Сегодня на уроке мы с вами будем учиться решать линейные уравнения с параметрами.

Задание 1

Рассмотрим уравнение mx + 3 = 4m – 2x. Оно содержит две переменные: m и x.

1. Вопрос. Чем же они отличаются? (одна из переменных, например m, принимает любые значения, тогда переменная x принимает не все значения, а только те, которые получаются при заданных значениях переменной m).

2. Задание. Решите данное уравнение при m = 2, – 1, 0.

если m = 2, то уравнение примет вид 2x + 3 = 8 – 2x. Ответ: ;
если m = – 1, то уравнение примет вид – x + 3 = – 4 – 2x. Ответ: – 7;
если m = 0, то уравнение примет вид 3 = – 2x. Ответ: – 1,5 )

3. Задание. Решите данное уравнение, задав свое значение для переменной m.
Переменную m, значения которой мы задаём, называют параметром (фиксированным числом).
Определение: решить уравнение с параметром – значит, для любых допустимых значений параметра найти значения неизвестной переменной.

4. Вопрос. Можем ли мы перебрать все значения параметра m, чтобы найти значения x? (нет)

5. Возникла проблемная ситуация. Как же решить данное уравнение mx + 3 = 4m – 2x?
Нет ли другого подхода к решению уравнения?
Оказывается существует. Для решения линейного уравнения с параметром применяется тот же
алгоритм решения, как и для линейного уравнения без параметра, т.е.перенос слагаемых и
приведение подобных слагаемых. Всегда ли эти операции выполняются? (да).
Выполним указанные операции:

6. Вопрос. Всегда ли можно выполнить деление? (нет).

7. Задание. Найдите контрольные значения, при которых уравнение не имеет решений.

Запишем решение уравнения далее так:

Задание 2 (разобрать так же подробно на доске)

Решите уравнение n 2 x + 3nx = 5n + 15;

n 2 x + 3nx = 5n + 15;
n (n + 3) x = 5 (n + 3);
n = – 3; 0 – контрольные значения параметра

1) при n = – 3 уравнение примет вид 0x = 0, x – любое число;
2) при n = 0 уравнение примет вид 0x = 15, решений нет;

Задание 3.

Самостоятельное решение уравнений с последующей проверкой на доске.

1. 2кx – 5(2 + x) = 7.

2кx – 5(2 + x) = 7;
2кx – 5x – 10 = 7;
2кx –5x = 7 + 10;
(2к –5) x = 17;
2к –5 = 0, к = 2,5 – контрольное значение параметра

1) при к = 2,5 уравнение примет вид 0x = 17, решений нет;

2. a 2 x – 2a = a 2 + ax

a 2 x – 2a = a 2 + ax;
a 2 x – ax = a 2 + 2a;
a(a – 1)x = a (a + 2);
a(a – 1) = 0, a = 0; 1 – контрольные значения параметра

1) при a = 0 уравнение примет вид 0x = 0, x – любое число;
2) при a = 1 уравнение примет вид 0x = 3, решений нет;

IV. Подведение итогов

1. Что мы сегодня рассматривали на уроке? (решение линейных уравнений с параметрами.)
2. В чем заключался алгоритм решения таких уравнений? Какие равносильные преобразования применяли?

а) освобождение от знаменателя, умножив обе части равенства на одно и тоже отличное от нуля число;
б) раскрытие скобок;
в) перенос слагаемых из одной части равенства в другую с противоположным знаком;
г) приведение подобных слагаемых.

V. Выставление оценок

VI. Домашнее задание

1) № 631; № 632; № 633.
2) Дополнительное задание

Источник

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

при а = 1 х – любое действительное число, кроме х = 1

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Источник

Линейное уравнение с параметром

Урок 18. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Линейное уравнение с параметром”

· рассмотреть линейные уравнения с параметрами;

· сформулировать алгоритм решения линейных уравнений с параметрами.

Уравнения, содержащие помимо неизвестных, ещё и буквенные величины называются уравнениями с параметрами.

Линейные уравнения, записанные в общем виде, рассматривают как уравнение с параметрами.

Как правило, для любого уравнения особым значением параметра является то, про котором коэффициент при переменной обращается в ноль.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Решим ещё одно уравнение.

Рассмотрим ещё одно уравнение.

Решим ещё один пример.

Теперь давайте попробуем сформулировать алгоритм решения линейных уравнений с параметром.

Сегодня на уроке мы рассмотрели линейные уравнения с параметрами, сформулировали алгоритм решения таких уравнений.

Источник