Линейные уравнения с параметром примеры с решением

Линейные уравнения с параметрами в 7-м классе (методические рекомендации)

Разделы: Математика

а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.

а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.

Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.

Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если а=10; а=-2; а=0.

Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра а

Как было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
Решение.1) (а2-1)=0, а=±1.
При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.

Задачи для самостоятельного решения.

Для всех значений параметров а и в решите уравнения:

Используемая литература.

Источник

Линейное уравнение с параметром

Урок 18. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Линейное уравнение с параметром»

· рассмотреть линейные уравнения с параметрами;

· сформулировать алгоритм решения линейных уравнений с параметрами.

Уравнения, содержащие помимо неизвестных, ещё и буквенные величины называются уравнениями с параметрами.

Линейные уравнения, записанные в общем виде, рассматривают как уравнение с параметрами.

Как правило, для любого уравнения особым значением параметра является то, про котором коэффициент при переменной обращается в ноль.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Решим ещё одно уравнение.

Рассмотрим ещё одно уравнение.

Решим ещё один пример.

Теперь давайте попробуем сформулировать алгоритм решения линейных уравнений с параметром.

Сегодня на уроке мы рассмотрели линейные уравнения с параметрами, сформулировали алгоритм решения таких уравнений.

Источник

Класс: 7

Презентация к уроку

Тип урока: введение нового материала.

Учебник: «Алгебра-7» авт. Ю.Н.Макарычев, Н.Г. Миндюк и др. издательство «Мнемозина», 2008 год.

I. Проверка домашнего задания (работа выполнялась на двойных листах и сдаётся на проверку).

Готовые решения проецируются на доску и разбирается (проговаривается) алгоритм решения.

№ 624. Решите уравнение:

а) 0,3(2x – 1) – 0,4 (x + 8) = 1,2x – 1;
0,6x – 0,3 – 0,4x – 3,2 = 1,2x – 1;
0,6x – 0,4x –1,2x = 0,3 + 3,2– 1;
– x = 2,5;
x = –2,5. Ответ: – 2,5.

в) – 6(2 – 0,2x) + 11 = – 4(3 – 0,3x) – 1;
– 12 + 1,2x + 11 = – 12 + 1,2x – 1;
1,2x – 1,2x = 12 – 11 + 1;
0x = 2. Ответ: решений нет.

№ 625. Решите уравнение

а) (2x – 1)(3x + 7) – (1 + 6x)(x + 2) = 4;
6x 2 + 14x – 3x – 7 – (x + 2 + 6×2 + 12x) = 4;
6x 2 + 14x – 3x – 7 – x – 2 – 6×2 – 12x = 4;
6x 2 + 14x – 3x – x – 6x 2 – 12x = 4 + 7 + 2;
– 2x = 13;
x = – 6,5. Ответ: – 6,5.

№ 626. Решите уравнение

№ 622. При каких значениях a уравнение ax = 2a – 1:

а) имеет единственный корень; (при a 0)
б) имеет бесконечно много корней; (таких значений a нет)
в) не имеет корней? (при a = 0).

II. Устная работа (задания проецируются на доску)

1. Найдите корни уравнения:

а) 14 + 3x = 5 – x ; (– 2,25)
б) 105y – 28 = 105y + 7;
в) 34x + 2 = 34x + 2. (x – любое число)

2. При каких значениях a число 3 является корнем уравнения?

3. Укажите контрольные значения, при которых уравнение не имеет решений или решением является любое число?

а) (5 – a) x = 0; б) (b + 4) x = 5; в) ax = x.

III. Изучение нового материала

Учитель. Сегодня на уроке мы с вами будем учиться решать линейные уравнения с параметрами.

Задание 1

Рассмотрим уравнение mx + 3 = 4m – 2x. Оно содержит две переменные: m и x.

1. Вопрос. Чем же они отличаются? (одна из переменных, например m, принимает любые значения, тогда переменная x принимает не все значения, а только те, которые получаются при заданных значениях переменной m).

2. Задание. Решите данное уравнение при m = 2, – 1, 0.

если m = 2, то уравнение примет вид 2x + 3 = 8 – 2x. Ответ: ;
если m = – 1, то уравнение примет вид – x + 3 = – 4 – 2x. Ответ: – 7;
если m = 0, то уравнение примет вид 3 = – 2x. Ответ: – 1,5 )

3. Задание. Решите данное уравнение, задав свое значение для переменной m.
Переменную m, значения которой мы задаём, называют параметром (фиксированным числом).
Определение: решить уравнение с параметром – значит, для любых допустимых значений параметра найти значения неизвестной переменной.

4. Вопрос. Можем ли мы перебрать все значения параметра m, чтобы найти значения x? (нет)

5. Возникла проблемная ситуация. Как же решить данное уравнение mx + 3 = 4m – 2x?
Нет ли другого подхода к решению уравнения?
Оказывается существует. Для решения линейного уравнения с параметром применяется тот же
алгоритм решения, как и для линейного уравнения без параметра, т.е.перенос слагаемых и
приведение подобных слагаемых. Всегда ли эти операции выполняются? (да).
Выполним указанные операции:

6. Вопрос. Всегда ли можно выполнить деление? (нет).

7. Задание. Найдите контрольные значения, при которых уравнение не имеет решений.

Запишем решение уравнения далее так:

Задание 2 (разобрать так же подробно на доске)

Решите уравнение n 2 x + 3nx = 5n + 15;

n 2 x + 3nx = 5n + 15;
n (n + 3) x = 5 (n + 3);
n = – 3; 0 – контрольные значения параметра

1) при n = – 3 уравнение примет вид 0x = 0, x – любое число;
2) при n = 0 уравнение примет вид 0x = 15, решений нет;

Задание 3.

Самостоятельное решение уравнений с последующей проверкой на доске.

1. 2кx – 5(2 + x) = 7.

2кx – 5(2 + x) = 7;
2кx – 5x – 10 = 7;
2кx –5x = 7 + 10;
(2к –5) x = 17;
2к –5 = 0, к = 2,5 – контрольное значение параметра

1) при к = 2,5 уравнение примет вид 0x = 17, решений нет;

2. a 2 x – 2a = a 2 + ax

a 2 x – 2a = a 2 + ax;
a 2 x – ax = a 2 + 2a;
a(a – 1)x = a (a + 2);
a(a – 1) = 0, a = 0; 1 – контрольные значения параметра

1) при a = 0 уравнение примет вид 0x = 0, x – любое число;
2) при a = 1 уравнение примет вид 0x = 3, решений нет;

IV. Подведение итогов

1. Что мы сегодня рассматривали на уроке? (решение линейных уравнений с параметрами.)
2. В чем заключался алгоритм решения таких уравнений? Какие равносильные преобразования применяли?

а) освобождение от знаменателя, умножив обе части равенства на одно и тоже отличное от нуля число;
б) раскрытие скобок;
в) перенос слагаемых из одной части равенства в другую с противоположным знаком;
г) приведение подобных слагаемых.

V. Выставление оценок

VI. Домашнее задание

1) № 631; № 632; № 633.
2) Дополнительное задание

Источник

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

Источник

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

при а = 1 х – любое действительное число, кроме х = 1

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

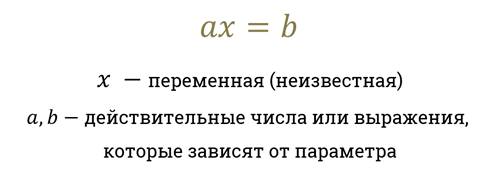
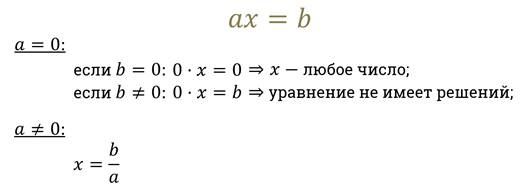
Источник