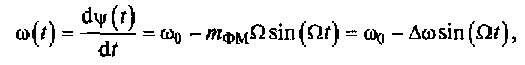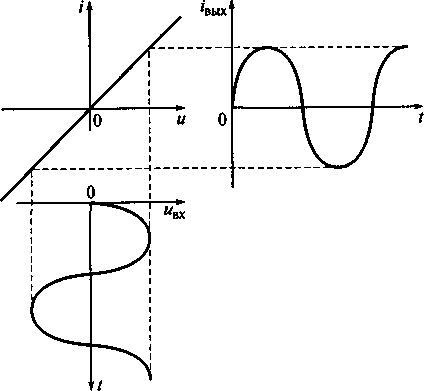Линия с сосредоточенными параметрами
Электрические цепи с сосредоточенными и распределенными параметрами
Электрические цепи с сосредоточенными и распределенными параметрами
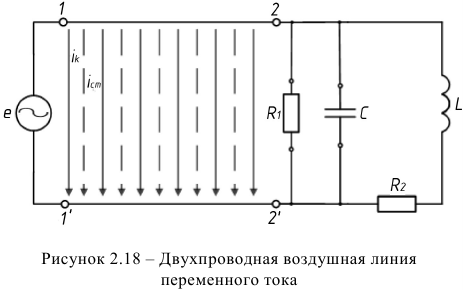
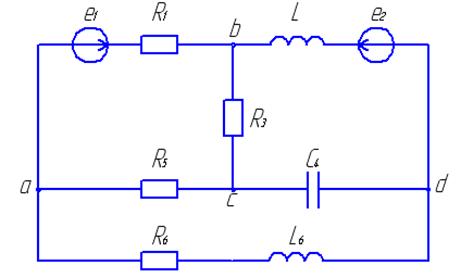
Рассмотренные в предыдущих параграфах пассивные идеальные элементы позволяют учитывать основные физические явления, протекающие в сложных электротехнических устройствах. Рассмотрим в качестве примера двухпроводную воздушную линию, соединяющую источник переменной ЭДС и приемник энергии (рисунок 2.18).
В соединительных проводах следует учитывать в общем случае четыре явления.
Электрическая цепь, в которой электрические сопротивления и проводимости, индуктивности и электрические емкости распределены вдоль линии, называют электрической цепью (линией) с распределенными параметрами.
Кроме приведенного примера к электрическим линиям с распределенными параметрами можно отнести реостаты, реальные индуктивные катушки и конденсаторы.
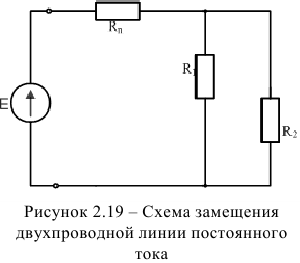
Далеко не во всех случаях необходимо учитывать все физические явления, происходящие в цепях переменного тока, что существенно упрощает задачу. Так, если в предыдущем примере величина напряжения источника питания малая, токи короны исчезают, а при постоянном характере ЭДС во времени исчезают токи электрического смещения и ЭДС самоиндукции. Схема замещения двухпроводной воздушной линии постоянного тока принимает упрощенный вид (рисунок 2.19), где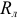 
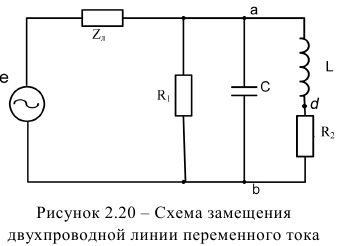
— резистор, учитывающий сопротивление току соединительного прямого и обратного проводов при малых значениях длины.
Схема замещения двухпроводной линии переменного тока с допущениями предыдущего примера представлена на рисунке 2.20, где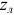 
— сопротивление прямого и обратного проводов соединительного провода.
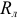
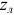
Не трудно заметить в схемах на рисунках 2.19 и 2.20 линия представлена в виде сосредоточенного сопротивления или .
Токи электрического смещения существуют только на участке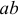 
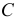
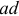
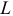
между обкладками конденсатора (рисунок 2.20), т.е. в этом участке сосредоточена емкость 
цепи. Наконец, предположим, что переменный магнитный поток индуцирует ЭДС только в катушке на участке 
, т.е., что в этом участке сосредоточена вся индуктивность 
цепи.
Электрические цепи, имеющие сложную конфигурацию и содержащие сосредоточенные резисторы, проводимости, индуктивности и электрические емкости только на отдельных участках и величина тока и потенциала, в общем случае, при переходе от одной точки к рядом расположенной непрерывно не изменяются для одного момента времени, называются электрическими цепями с сосредоточенными параметрами.
Приняв сделанные допущения, мы получаем возможность рассматривать теорию электрических цепей с сосредоточенными параметрами, охватывающую большой класс реальных электрических цепей, за исключением длинных линий передачи энергии и протяженных линий связи.
Электрическую цепь можно рассматривать как цепь с сосредоточенными параметрами, если изменения напряжений и токов в соединительных проводах цепи столь малы, что за время распространения электромагнитной волны вдоль всей цепи в любом направлении изменения величин напряжений и токов остаются малыми.
Эта страница взята со страницы задач по электротехнике:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Частотная характеристика соизмеримых линейных цепей, как и всех цепей с распределенными элементами, будет периодически повторяться, ограничивая частотный диапазон, в котором они действуют. Схемы, разработанные по методикам Ричардса и Курода, не самые компактные. Усовершенствования методов соединения элементов вместе могут привести к созданию более компактных конструкций. Тем не менее теория соразмерных линий остается основой для многих из этих более совершенных конструкций фильтров.
СОДЕРЖАНИЕ
Соразмерные линии
Преимущество использования соразмерных линий состоит в том, что теория соразмерных линий позволяет синтезировать схемы на основе заданной частотной функции. Хотя любую схему, использующую линии передачи произвольной длины, можно проанализировать для определения ее частотной функции, эту схему не обязательно легко синтезировать, исходя из частотной функции. Основная проблема заключается в том, что для использования более одной длины обычно требуется более одной частотной переменной. Для использования соразмерных линий требуется только одна частотная переменная. Существует хорошо разработанная теория синтеза схем с сосредоточенными элементами на основе заданной частотной функции. Любую синтезированную таким образом схему можно преобразовать в соизмеримую линейную схему с помощью преобразования Ричардса и новой переменной частоты.
Преобразование Ричардса
Ричардс преобразования преобразует угловую частоту переменного, со, в соответствии с,
Сравнивая это преобразование с выражениями для вождения точки импеданса от окурков прерванных, соответственно, короткого замыкания и обрыва цепи,
Это часто записывается как,
L и C обычно обозначают индуктивность и емкость, но здесь они представляют соответственно характеристическое сопротивление индуктивного шлейфа и характеристическую проводимость емкостного шлейфа. Это соглашение используется многими авторами и далее в этой статье.
Омега-домен
Преобразование Ричардса можно рассматривать как преобразование из представления s-области в новую область, называемую Ω-областью, где,
и длина в единицах расстояния становится,
Каскадный элемент
Личности Куроды
Тождества Куроды представляют собой набор из четырех эквивалентных схем, которые преодолевают определенные трудности с прямым применением преобразований Ричардса. Четыре основных преобразования показаны на рисунке. Здесь символы конденсаторов и катушек индуктивности используются для обозначения шлейфов разомкнутой цепи и короткого замыкания. Аналогично, символы C и L здесь обозначают, соответственно, восприимчивость шлейфа разомкнутой цепи и реактивное сопротивление шлейфа короткого замыкания, которые для θ = λ / 8 соответственно равны характеристической проводимости и характеристическому сопротивлению шлейфа. Прямоугольники с толстыми линиями представляют собой каскад, соединенный соразмерными длинами линий с отмеченным характеристическим сопротивлением.
Первая решаемая трудность заключается в том, что все UE должны быть соединены вместе в одной точке. Это возникает из-за того, что модель с сосредоточенными элементами предполагает, что все элементы занимают нулевое пространство (или не занимают значительного пространства) и что нет задержки в сигналах между элементами. Применение преобразования Ричардса для преобразования схемы с сосредоточенными параметрами в распределенную схему позволяет элементу теперь занимать конечное пространство (его длину), но не отменяет требования нулевого расстояния между соединениями. Путем многократного применения первых двух идентификаторов Курода длины UE линий, идущих в порты схемы, можно перемещать между компонентами схемы для их физического разделения.
Третья и четвертая идентичности позволяют уменьшать или увеличивать характеристические импедансы соответственно. Они могут быть полезны для преобразования импедансов, которые непрактично реализовать. Однако у них есть недостаток, заключающийся в необходимости добавления идеального трансформатора с коэффициентом масштабирования, равным коэффициенту масштабирования.
История
В течение десятилетия после публикации Ричардса успехи в теории распределенных схем имели место в основном в Японии. К. Курода опубликовал эти личности в 1955 году в своей докторской диссертации. Однако они не появлялись на английском языке до 1958 года в статье Одзаки и Исии о полосовых фильтрах.
Дальнейшие уточнения
Ширина спектра ЧМ-колебания с малым индексом модуляции равна 2Ω, т.е. определяется шириной спектра модулирующего сигнала. В случае большого индекса модуляции ширина спектра ЧМ-колебания равна 2∆ω и определяется девиацией частоты (4.15).
4.7. Фазовая модуляция
Фазомодулированный сигнал описывается выражением (4.10). Его мгновенная фаза согласно (4.9) определяется из выражения
(4.18)
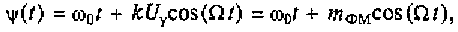
где mфн = kUy— коэффициент фазовой модуляции.
В соответствии с (4.18) мгновенная частота ФМ-сигнала
где ∆ω = kUyΩ — девиация частоты при фазовой модуляции.
ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
ЛИНЕЙНЫЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
5.1. Классификация радиотехнических цепей
Радиотехническими цепями называют электрические цепи, применяемые в радиоэлектронных устройствах. Поэтому анализ радиотехнических цепей базируется на использовании общей теории электрических цепей.
Радиотехнические цепи классифицируются по следующим признакам.
1. По числу внешних выводов (полюсов, портов) цепи, которыми данная цепь соединяется с источниками сигналов, нагрузочными элементами или другими электрическими цепями.
2. По наличию источника энергии внутри радиотехнической цепи (цепь активная, если имеется источник энергии, пассивная цепь — при его отсутствии).
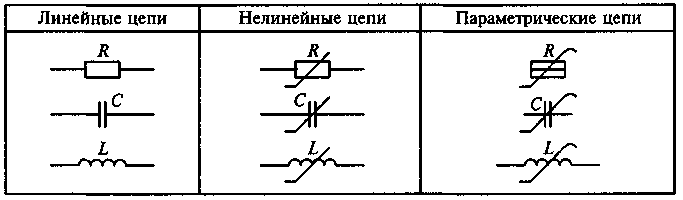
3. По характеру процессов, протекающих в цепи, реакции (отклику) цепи на внешнее воздействие. В линейной цепи (табл. 5.1) зависимость напряжения, тока или мощности отклика цепи от внешнего воздействия носит линейный характер. В нелинейной цепи (см. табл. 5.1) вольт-амперная характеристика (ВАХ) хотя бы одного элемента носит нелинейный характер. И, наконец, в параметрической цепи имеется хотя бы один элемент, у которого один или несколько параметров зависят от времени.
Графические обозначения элементов радиотехнических цепей
4. По сосредоточенным либо распределенным параметрам.
Под цепью с сосредоточенными параметрами понимают цепь, в которой выделяется конечное число элементов (участков) с геометрическими размерами, существенно меньшими длины электромагнитной волны. К таким элементам цепи относят индуктивные катушки, конденсаторы, резисторы и т.д.
Цепи, в которых геометрические размеры элементов (участков.) превышают длину электромагнитной волны, называются цепями с распределенными параметрами. К таким элементам цепи относят, например, волноводы и коаксиальные кабели.
Линейными называются цепи, состоящие только из линейных элементов, под которыми понимают элементы с параметрами, остающимися постоянными при приложении к ним напряжения и или тока i и не зависящими от их значений и направления. К линейным элементам (двухполюсным) можно отнести резистор R, индуктивную катушку Lи конденсатор С.
Так, для любой точки ВАХ резистора отношение напряжения к току u/i согласно закону Ома, равно сопротивлению Rэтого резистора и представляет собой постоянную величину. ВАХ подобного резистора носит линейный характер. На рис 5.1 показан процесс формирования выходного тока в линейной цепи при воздействии гармонического сигнала. При приложении к этой цепи синусоидального напряжения с фиксированной частотой на выходе цепи появится ток, имеющий вид гармонической функции той же частоты, что и напряжение.
Рис. 5.1. Процесс формирования выходного тока в линейной цепи
при воздействии гармонического сигнала
Для постоянного конденсатора линейный характер имеет кулон-вольтная характеристика, т.е. зависимость заряда, накапливаемого в конденсаторе, от напряжения, приложенного к нему. Для индуктивной катушки линейный характер носит вебер-амперная xарактеристика, т.е. зависимость заряда, накапливаемого в индуктивной катушке, от тока, протекающего через нее.
Отличительной чертой линейных цепей является то, что они подчиняются принципу суперпозиции (наложения): при воздействии на цепь нескольких ЭДС любой формы и частоты отклики на каждую из ЭДС не зависят друг от друга. Полный отклик на выходе линейной цепи представляется суммой этих откликов. Например, так как сопротивление линейной цепи не зависит от приложенного напряжения, то любая вводимая в такую цепь ЭДС приведет к пропорциональному приращению тока. Соответственно и результирующий ток в резисторе будет равен сумме токов, вызываемых отдельными ЭДС.
Нелинейными цепями называют такие цепи, в которые входят один или несколько нелинейных элементов, под которыми понимают элементы с параметрами, зависящими от напряжений и токов, приложенных к ним. Например, к числу нелинейных элементов можно отнести полупроводниковый диод, ВАХ которого носит нелинейный характер. На рис. 5.2, а показаны графическое обозначение и ВАХ полупроводникового диода. Напряжение, приложенное к диоду, и ток, протекающий через него, связаны нелинейной зависимостью (рис. 5.2, б).
Чтобы распечатать файл, скачайте его (в формате Word).
Цепи с распределенными и с сосредоточенными параметрами
Если электрическая цепь содержит хотя бы один элемент с распределенными параметрами, то эта цепь называется цепью с распределенными параметрами. В противном случае цепь с сосредоточенными параметрами.
Элемент с сосредоточенными параметрами – это такой элемент, размеры которого не влияют на физические процессы в нем. К элементам с распределенными параметрами относятся линии передач, антенны. Если размеры элемента влияют на физические процессы, то это элемент с распределенными параметрами. В основном большинство элементов будем считать элементами с сосредоточенными параметрами.
Все высказанные выше определения достаточно условны. Один и тот же элемент в той или иной степени описания процесса на нем может быть отнесен к линейным или нелинейным, с распределенными или сосредоточенными параметрами.
В дальнейшем мы будем изучать линейные цепи с сосредоточенными параметрами.
Электрическая схема
Графическое изображение электрической цепи называется электрической схемой. На электрических схемах различают 3 элемента:
1. Ветвь – это последовательное соединение элементов, по которым протекает один и тот же ток.
2. Узел – это место электрической схемы, где сходится 3 и более ветвей.
3. Контур – это замкнутый участок цепи.
— ветви;
— узлы;
— замкнутые контуры.
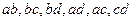
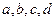
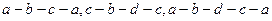
Число независимых контуров – это минимальное количество контуров, из которых может быть составлена рассматриваемая схема.
Обозначим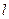 
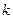
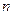
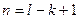
— число ветвей, 
— число узлов, 
— число независимых контуров, которое определяется по формуле 
.
Положительные направления токов, падений напряжений и э.д.с.
Обычно при анализе электрических цепей произвольно выбирается положительное направление токов в ветвях. Затем в зависимости от выбранных положительных направлений токов определяются положительные направления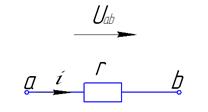 
падений напряжений на элементах. Рассмотрим отдельные элементы.
Это значит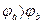 
, 
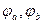
— потенциалы точек а и b.
Падение напряжений – это разность потенциалов, т.е.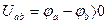 
, 
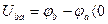
. То же самое будет на катушке индуктивности и конденсаторе.
Таким образом, положительное направление падения напряжения на пассивных элементах совпадает с положительным направлением тока через них.
Рассмотрим активный элемент – источник э.д.с.
, — потенциалы точек а и b.Тогда 
, 
.
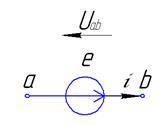
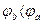
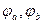
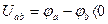
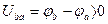
Таким образом, положительное направление падения напряжения на источнике э.д.с. противоположно положительному направлению э.д.с.
Пример:
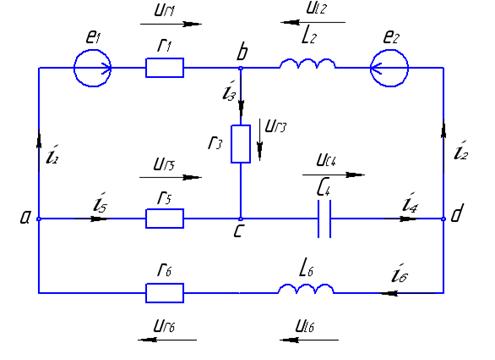
2.2 Электрические цепи с сосредоточенными параметрами.
Пассивные электрические цепи могут быть с сосредоточенными и распределенными параметрами.
Цепь состоит из источников R,L,C и соединительных проводов.
Если не выполнено хотя бы одно из перечисленных условий, то цепь следует рассматривать как цепь с распределенными параметрами.
Свойства цепи с сосредоточенными параметрами:
1)Если в данной цепи провести ряд сечений и включить в данное сечение А, то ток во всех точках в один и тот же момент окажется одинаковым.
2)Такая цепь не излучает в окружающее пространство электромагнитную энергию, все процессы сосредоточены внутри цепи.
Возникает вопрос: как разбивать схему для анализа?
В данной схеме, как источник u(t) поставляющий энергию в цепь, так и расходующий её пассивный элемент могут рассматриваться либо как элементы, в ходящие в состав данной цепи, либо как внешние по отношению к ней. В простейших случаях резистор считают элементом цепи, а источник внешним по отношению к ней.
Если электрическая цепь подключается к внешним элементам в двух точках (точка 1и 1’ на рисунке 2.1), то она называется двухполюсной.
Схему 2.1 можно считать как 2 двухполюсника
2.3 Электрические цепи с распределенными параметрами
Линия передает часть энергии в окружающее пространство в виде излучения.
рис 2.2
В цепи с сосредоточенными параметрами в любом сечении в один и тот же момент времени будет один и тот же ток, а в цепи с распределенными параметрами в разных сечениях в один и тот же момент времени будет разный ток.