Логарифмические уравнения и неравенства с параметром

Логарифмические уравнения, неравенства и системы с параметром

п.1. Примеры

Ответ:
При \(a\leq 1\cup a\gt 100\) решений нет, \(x\in\varnothing\)
При \(a=100\) один корень \(x=1\)
При \(1\lt a\lt 100\) два корня \(x_<1,2>=1\pm\sqrt<1-\frac<\lg a><2>>\)

б) \( x^<\log_a x>=a^2 x \)
ОДЗ: \( \begin x\gt 0\\ a\gt 0\\ a\ne 1 \end \)
Замена: \(t=\log_a x\Rightarrow x=a^t.\) Подставляем: \begin (a^t)^t=a^2\cdot a^t\Rightarrow a^=a^<2+t>\Rightarrow\\ \Rightarrow t^2=2+t\Rightarrow t^2-t-2=0\Rightarrow (t+1)(t-2)=0\Rightarrow \left[ \begin t_1=-1\\ t_2=2 \end \right. \end Возвращаемся к исходной переменной: \begin \left[ \begin \log_a x=-1\\ \log_a x=2 \end \right. \Rightarrow \left[ \begin x_1=a^<-1>=\frac1a\\ x_2=a^2 \end \right. \end Ответ:
При \(0\lt a\lt 1\cup a\gt 1\) два корня \(x_1=\frac1a,\ x_2=a^2\)
При \(a\lt 0\cup a=1\) решений нет.

Пример 2. Решите неравенство:
a) \( \log_a(x-1)+\log_a x\gt 2 \)
\(\log_a(x(x-1))\gt\log_a a^2\) \begin \left[ \begin \begin a\gt 1\\ x-1\gt 0\\ x\gt 0\\ x^2-x\gt a^2 \end \\ \begin 0\lt a\lt 1\\ x-1\gt 0\\ x\gt 0\\ x^2-x\lt a^2 \end \end \right. \Rightarrow \left[ \begin \begin a\gt 1\\ x\gt 1\\ x^2-x-a^2\gt 0 \end \\ \begin 0\lt a\lt 1\\ x-1\gt 0\\ x\gt 1\\ x^2-x-a^2\lt 0 \end \end \right. \end Исследуем параболу \(f(x)=x^2-x-a^2\)
\(D=1+4a^2\gt 0, \forall a\)
\(x_<1,2>=\frac<1\pm\sqrt<1+4a^2>><2>\)
Эта парабола всегда имеет две различных точки пересечения с осью OX.
\(f(x)\gt 0\), при \(x\lt x_1\cup x\gt x_2\)
\(f(x)\lt 0\), при \(x_1\lt x\lt x_2\)
Подставляем в совокупность: \begin \left[ \begin \begin a\gt 1\\ x\gt 1\\ x\lt\frac<1-\sqrt<1+4a^2>><2>\cup x\gt\frac<1+\sqrt<1+4a^2>> <2>\end \\ \begin 0\lt a\lt 1\\ x\gt 1\\ \frac<1-\sqrt<1+4a^2>><2>\lt x\lt \frac<1+\sqrt<1+4a^2>> <2>\end \end \right. \Rightarrow \left[ \begin \begin a\gt 1\\ x\gt \frac<1+\sqrt<1+4a^2>> <2>\end \\ \begin 0\lt a\lt 1\\ a\lt x\lt \frac<1+\sqrt<1+4a^2>> <2>\end \end \right. \end Ответ:
При \(a\gt 1\) луч \(x\in\left(\frac<1+\sqrt<1+4a^2>><2>;+\infty\right)\)
При \(0\lt a\lt 1\) интервал \(x\in\left(1;\frac<1+\sqrt<1+4a^2>><2>\right)\)
При \(a\leq 0\cup a=1\) решений нет.

б) \( \log_x(x-a)\gt 2 \)
\(\log_x(x-a)\gt\log_x x^2\) \begin \left[ \begin \begin x\gt 1\\ x-a\gt x^2\\ x-a\gt 0 \end \\ \begin 0\lt x\lt 1\\ x-a\lt x^2\\ x-a\gt 0 \end \end \right. \Rightarrow \left[ \begin \begin x\gt 1\\ x^2-x+a\lt 0\\ x\gt a \end \\ \begin 0\lt x\lt 1\\ x^2-x+a\gt 0\\ x\gt a \end \end \right. \end Исследуем параболу \(f(x)=x^2-x+a\)
\(D=1-4a\)

в) \( \frac<\log_a(35-x^3)><\log_a(5-x)>\gt 3 \) \begin \frac<\log_a(35-x^3)><\log_a(5-x)>-3\gt 0\\ \frac<\log_a(35-x^3)-3\log_a(5-x)><\log_a(5-x)>\gt 0\\ \left[ \begin \begin \log_a(35-x^3)\gt 3\log_a(5-x)\\ \log_a(5-x)\gt 0 \end \\ \begin \log_a(35-x^3)\lt 3\log_a(5-x)\\ \log_a(5-x)\lt 0 \end \end \right. \Rightarrow \left[ \begin \begin \log_a(35-x^3)\gt \log_a(5-x)^3\\ \log_a(5-x)\gt 0 \end \\ \begin \log_a(35-x^3)\lt \log_a(5-x)^3\\ \log_a(5-x)\lt 0 \end \end \right. \Rightarrow \\ \Rightarrow \left[ \begin \begin a\gt 1\\ \left[ \begin \begin 35-x^3\gt(5-x)^3\gt 0\\ 5-x\gt 1 \end \\ \begin 0\lt 35-x^3\lt(5-x)^3\\ 0\lt 5-x\lt 1 \end \end \right. \end \\ \begin 0\lt a\lt 1\\ \left[ \begin \begin 0\lt 35-x^3\lt(5-x)^3\\ 0\lt 5-x\lt 1 \end \\ \begin 35-x^3\gt (5-x)^3\gt 0\\ 5-x\gt 1 \end \end \right. \end \end \right. \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin \begin 35-x^3\gt(5-x)^3\gt 0\\ 5-x\gt 1 \end \\ \begin 0\lt 35-x^3\lt (5-x)^3\\ 0\lt 5-x\lt 1 \end \end \right. \end \end Решим основное неравенство: \begin 35-x^3\gt(5-x)^3\\ 35-x^3\gt 125-75x+15x^2-x^3\\ 15x^2-75x+90\lt 0\\ x^2-5x+6\lt 0\\ (x-2)(x-3)\lt 0\\ 2\lt x\lt 3 \end Подставляем в систему: \begin \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin \begin 2\lt x\lt 3\\ x\lt 4 \end \\ \begin x\lt 2\cup x\gt 3\\ x\lt\sqrt[3]<35>\\ 4\lt x\lt 5 \end \end \right. \end \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin 2\lt x\lt 3\\ \varnothing \end \right. \end \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ 2\lt x\lt 3 \end \end Ответ:
При \(0\lt a\lt 1\cup a\gt 1,\ x\in(2;3)\)
При \(a\leq 0\cup a=1\) решений нет

Источник

Занятие по программе элективного курса “Решение логарифмических, показательных уравнений, неравенств с параметрами”

Разделы: Математика

1. Введение

2. Показательные и логарифмические уравнения

Рассмотрим решение показательных и логарифмических уравнений с параметром на конкретных примерах.

Найти все значения параметра a, при которых уравнение 21g(x + 3) = lg ax имеет единственный корень.

Решите следующие примеры самостоятельно.

2. Найти все значения параметра, при каждом из которых уравнение log₃(9 x + 9a 3 ) = x имеет два различных решения.

3. Решите уравнение

.

4. Решите уравнение

.

9. Решите уравнение

.

10. Решите уравнение

.

4. При a ∈ (0; 1) ∪ (1; +∞) x = 3 / 4.

5. При

, при m = 1 x = 1, при

, при m ∈ [-1; 1] x ∈ ∅.

7. При a ∈ (-∞; 1 / 4]

.

9. При

.

3. Показательные и логарифмические неравенства

Решите неравенство

.

При a ≤ 0 и a = 0 показательная функция не определена, следовательно, неравенство не имеет решения.

Рассмотрим решение неравенства при a > 0, a ≠ 1

.

Введем вспомогательную переменную a x = z.

Тогда неравенство принимает вид

или

.

Решив алгебраическое неравенство методом интервалов, получим z ∈ (-∞; 1 / 2) ∪ (1; 2),

или

.

Монотонность показательной функции зависит от величины основания, следовательно,

при a ∈ (0; 1) совокупность неравенств принимает вид

,

а при a ∈ (1; +∞)

.

2. При каких значениях параметра неравенство

верно при любом действительном значении x?

6. Найдите все действительные значения параметра, при которых неравенство 1 + log₂(2x 2 + 2x + 7 / 2) ≥ log₇(cx 2 + c) имеет хотя бы одно решение.

Источник

Методическая разработка для учащихся 11-го класса “Решение логарифмических уравнений с параметром”

Разделы: Математика

Ученик проходит в несколько лет
дорогу, на которую человечество
употребило тысячелетие.
Однако его следует вести к цели
не с завязанными глазами, а
зрячим: он должен воспринимать
истину, не как готовый результат,
а должен её открывать.
Учитель должен руководить этой
экспедицией открытий, следовательно,
также присутствовать не только в качестве простого зрителя.
Но ученик должен напрягать свои силы; ему ничто не должно
доставаться даром. Даётся только тому, кто стремится.

Кто любит учиться, никогда
не проводит время в праздности.

Гений состоит из одного процента вдохновения и девяноста девяти процентов потения.

К сожалению, изучению этих трёх типов решения логарифмических уравнений с параметрами в программе общеобразовательной школы уделяется незаслуженно мало внимания. А подобные уравнения входят в сложную группу заданий, предлагаемых в рамках ЕГЭ, для решения которых необходима хорошая теоретическая подготовка учащихся и уверенное владение технологиями решения математических задач. Выпускник должен не только знать обязательные этапы решения логарифмических уравнений с параметрами, но и хорошо понимать их смысл и назначение, так как многие учащиеся понимают параметр, как «обычное число». Действительно, в некоторых задачах параметр можно считать постоянной величиной, но эта постоянная величина принимает неизвестные значения. Поэтому необходимо рассматривать задачу при всех возможных значениях этой постоянной. В других задачах параметром бывает удобно объявить одну из неизвестных.
На вступительных экзаменах в высшие учебные заведения в виде ЕГЭ встречаются два типа задач с параметрами. Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям». Соответственно и ответы в задачах этих двух типов различаются по существу. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
Основная цель данной методической разработки: научить учащихся решать нестандартные логарифмические уравнения с параметром, показать разные методы их решений, сделать использование этих методов глубоко осмысленными.
Предлагаемые в этой методической разработке методы решения уравнений не сказочный ключ к решению любой задачи. Но они направляют мысль, сокращают время поиска, формируют навыки решения. Все предлагаемые уравнения снабжены подробными решениями. Показано решение 18 уравнений. Но чтобы получить ощутимую пользу от знакомства с готовым решением, необходимо, уловив новую идею, удержаться и не читать дальше, и попробовать затем решать самостоятельно.

При решении логарифмических уравнений с параметрами необходимо придерживаться следующей схемы:

1. Найти область допустимых значений.
2. Решить уравнение (чаще всего выразить х через а).
3. Сделать перебор параметра а с учетом ОДЗ.
4. Проверить, удовлетворяют ли найденные корни уравнения условиям ОДЗ.
5. Записать ответ.

Источник

Логарифмические уравнения с параметром

Содержимое разработки

Логарифмические уравнения с параметром.

Областью определения его служит решение системы

При a = b мы получим уравнение f(x) = g(x) , равносильное исходному.

При a = b мы получим уравнение f(x) = g(x) , равносильное исходному.

При a ≠ b решение уравнения сводится к решению уравнения

При решении логарифмических уравнений с параметрами необходимо придерживаться следующей схемы:

1. Найти область допустимых значений. 2. Решить уравнение (чаще всего выразить x через a). 3. Сделать перебор параметра a с учетом ОДЗ. 4. Проверить, удовлетворяют ли найденные корни уравнения условиям ОДЗ. 5. Записать ответ.

Типы логарифмических уравнений с параметром:

0 (a ≠ 1 ), 2. ” width=”640″

Источник

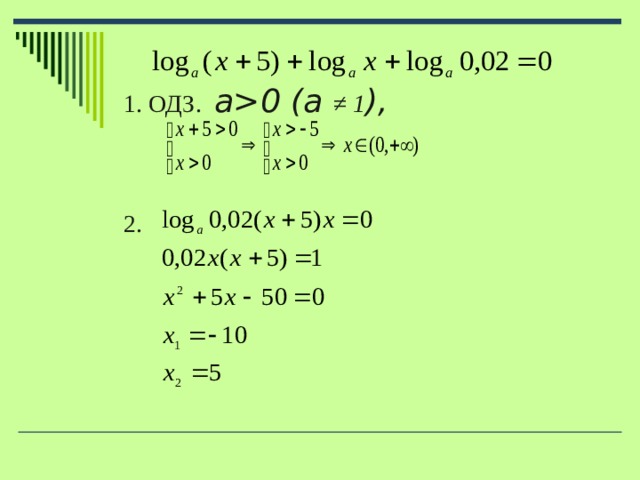
Учебное пособие “Уравнения и неравенства с параметрами”

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В. Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

« Уравнения и неравенства с параметрами» для учащихся 10 –11 классов

данное пособие является приложением к программе элективного курса «Уравнения и неравенства с параметрами», которая прошла внешнюю экспертизу (научно-методическим экспертным советом министерства образования и науки Самарской области от 19 декабря 2008 года бала рекомендована к использованию в образовательных учреждениях Самарской области)

Авторы

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Ромаданова Ирина Владимировна

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Сербаева Ирина Алексеевна

Линейные уравнения и неравенства с параметрами……………..4-7

Квадратные уравнения и неравенства с параметрами……………7-9

Дробно- рациональные уравнения с параметрами……………..10-11

Иррациональные уравнения и неравенства с параметрами……11-13

Тригонометрические уравнения и неравенства с параметрами.14-15

Показательные уравнения и неравенства с параметрами………16-17

Логарифмические уравнения и неравенства с параметрами…. 16-18

Задания для самостоятельной работы…………………………. 21-28

Уравнения и неравенства с параметрами.

Если в уравнении или неравенстве некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Для того, чтобы решить уравнение или неравенство с параметрами необходимо:

Определить допустимые значения – это значения параметра, при которых уравнение или неравенство имеет смысл.

Решить уравнение или неравенство с параметрами означает:

1) определить, при каких значениях параметров существуют решения;

2) для каждой допустимой системы значений параметров найти соответствующее множество решений.

Решить уравнение с параметром можно следующими методами: аналитическим или графическим.

Аналитический метод предполагает задачу исследования уравнения рассмотрением нескольких случаев, ни один из которых нельзя упустить.

Решение уравнения и неравенства с параметрами каждого вида аналитическим методом предполагает подробный анализ ситуации и последовательное исследование, в ходе которого возникает необходимость «аккуратного обращения» с параметром.

Графический метод предполагает построение графика уравнения, по которому можно определить, как влияет соответственно, на решение уравнения изменение параметра. График подчас позволяет аналитически сформулировать необходимые и достаточные условия для решения поставленной задач. Графический метод решения особенно эффективен тогда, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра и обладает несомненным преимуществом увидеть это наглядно.

§ 1. Линейные уравнения и неравенства.

Линейное уравнение а x = b , записанное в общем виде, можно рассматривать как уравнение с параметрами, где x – неизвестное, a , b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра a является значение а = 0.

Если а ¹ 0, то при любой паре параметров а и b оно имеет единственное решение х=.

b = 0 является особым значением параметра b .

При b ¹ 0 уравнение решений не имеет.

При b = 0 уравнение примет вид: 0х = 0. Решением данного уравнения является любое действительное число.

Неравенства вида ах > b и ax b ( а ≠ 0) называются линейными неравенствами. Множество решений неравенства ах > b – промежуток

ах b множество решений – промежуток (-;), если a > 0, и (; +), если а

Пример 1. Решить уравнение ах = 5

Если а = 0, то уравнение 0 × х = 5 решения не имеет.

Ответ: при а ¹ 0, х=

при а = 0 решения нет.

Пример 2. Решить уравнение ах – 6 = 2а – 3х.

Решение: Это линейное уравнение, ах – 6 = 2а – 3х (1)

ах + 3х = 2а +6

Переписав уравнение в виде (а+3)х = 2(а+3), рассмотрим два случая:

Пример 3. При каких значениях параметра а среди корней уравнения

Решение: Решим уравнение 2ах – 4х – а 2 + 4а – 4 = 0 – линейное уравнение

При а = 2 решением уравнения 0х = 0 будет любое число, в том числе и большее 1.

При а ¹ 2 х =. По условию х > 1, то есть >1, а > 4.

Ответ: При а <2>U (4;∞).

Пример 4. Для каждого значения параметра а найти количество корней уравнения ах=8.

Решение. ах = 8 – линейное уравнение.

а =,

y = a – семейство горизонтальных прямых;

y = – графиком является гипербола. Построим графики этих функций.

Ответ: Если а =0, то уравнение решений не имеет. Если а ≠ 0, то уравнение имеет одно решение.

Пример 5. С помощью графиков выяснить, сколько корней имеет уравнение:

y = ах – 1 – графиком является прямая, проходящая через точку (0;-1).

Построим графики этих функций.

Ответ:При|а|>1– один корень

при | а|≤1 – уравнение корней не имеет.

Решение : ах + 4 > 2х + а 2 (а – 2) х > а 2 – 4. Рассмотрим три случая.

а > 2. (а – 2) х > ( а – 2)(а + 2) х > а + 2

а (а – 2) х > ( а – 2)(а + 2) х а + 2

Ответ. х > а + 2 при а > 2; х при а при а=2 решений нет.

§ 2. Квадратные уравнения и неравенства

Для решения квадратных уравнений с параметром можно использовать стандартные способы решения на применение следующих формул:

2) формул корней квадратного уравнения: х ₁ =, х ₂ =,

(х _{1,2 =} )

Квадратными называются неравенства вида

Множество решений неравенства (3) получается объединением множеств решений неравенства (1) и уравнения , a х 2 + b х + с=0. Аналогично находится множество решений неравенства (4).

Если квадратный трехчлен имеет корни (х _{1 2} ), то при а > 0 он положителен на множестве (-; х ₂ )( х _2; +) и отрицателен на интервале

(х ₁ ; х ₂ ). Если а ₁ ; х ₂ ) и отрицателен при всех х (-; х ₁ )( х _2; +).

Это квадратное уравнение

Решение: Особое значение а = 0.

При а = 0 получим линейное уравнение 2х – 4 = 0. Оно имеет единственный корень х = 2.

При а ≠ 0. Найдем дискриминант.

Пример 2. Найдите количество корней данного уравнения х²-2х-8-а=0 в зависимости от значений параметра а.

Решение. Перепишем данное уравнение в виде х²-2х-8=а

y = х²-2х-8– графиком является парабола;

y =а– семейство горизонтальных прямых.

Построим графики функций.

Решение. Квадратный трехчлен положителен при всех значениях х, если

§ 3. Дробно- рациональные уравнения с параметром,

сводящиеся к линейным

Процесс решения дробных уравнений выполняется по обычной схеме: дробное заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решается целое уравнение, исключая посторонние корни, то есть числа, которые обращают знаменатель в нуль.

В случае уравнений с параметром эта задача более сложная. Здесь, чтобы «исключить» посторонние корни, требуется найти значение параметра, обращающее общий знаменатель в нуль, то есть решить соответствующие уравнения относительно параметра.

Пример 1. Решить уравнение = 0

Это дробно- рациональное уравнение

Пример 2 . Решить уравнение– = (1)

Это дробно- рациональное уравнение

При переходе от уравнения (1) к уравнению (2) расширилась область определения уравнения (1), что могло привести к появлению посторонних корней. Поэтому, необходима проверка.

П р о в е р к а. Исключим из найденных значений х такие, при которых

х ₁+1=0, х ₁+2=0, х₂+1=0, х₂+2=0.

Если х₂+1=0, то есть (а – 3) + 1= 0, то а = 2. Таким образом, при а = 2 х₂ – посторонний корень уравнения (1).

Если х₂+2=0, то есть (а – 3) + 2 = 0, то а=1. Таким образом, при а = 1,

Можно записать ответ.

§4. Иррациональные уравнения и неравенства

Уравнения и неравенства, в которых переменная содержится под знаком корня, называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение, учитывая при этом изменения значений параметра.

Уравнение вида = g ( x ) равносильно системе

Неравенство f ( x ) ≥ 0 следует из уравнения f ( x ) = g 2 ( x ).

При решении иррациональных неравенств будем использовать следующие равносильные преобразования:

≤ g(x) ≥g(x)

Пример 1. Решите уравнение = х + 1 (3)

Это иррациональное уравнение

Решение: По определению арифметического корня уравнение (3) равносильно системе .

При а = 2 первое уравнение системы имеет вид 0 х = 5, то есть не имеет решений.

откуда а ≤ или а > 2.

Ответ: При а≤, а > 2 х= , при уравнение решений не имеет.

Пример 2. Решить уравнение = а (приложение 4)

Решение. y =

y = а – семейство горизонтальных прямых.

Построим графики функций.

Решение. О.Д.З. х ≤ 2. Если а+1 ≤0, то неравенство выполняется при всех допустимых значениях х. Если же а+1>0, то

(а+1)

откуда х (2- 2

§ 5. Тригонометрические уравнения и неравенства.

Приведем формулы решений простейших тригонометрических уравнений:

Sinx = a x= (-1) n arcsin a+πn, n Z, ≤1, (1)

tg x = a x= arctg a + πn, n Z, aR

ctg x = a x = arcctg a + πn, n Z, aR

Для каждого стандартного неравенства укажем множество решений:

1. sin x > a arcsin a + 2 πn Z,

при a xR ; при a ≥ 1, решений нет.

при а≤-1, решений нет; при а >1, xR

3. cos x > a – arccos a + 2 πn x arccos a + 2 πn , n Z ,

5. tg x > a, arctg a + πnZ

Пример1. Найти а, при которых данное уравнение имеет решение:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Решение. Запишем уравнение в виде

Ответ. а -2; 0 4; 6

Пример 2. При каких b найдется а такое, что неравенство + b > 0 выполняется при всех х ≠ πn , n Z .

Решение. Положим а = 0. Неравенство выполняется при b >0. Покажем теперь, что ни одно b ≤0 не удовлетворяет условиям задачи. Действительно, достаточно положить х = π /2, если а π /2 при а ≥0.

§ 6. Показательные уравнения и неравенства

1. Уравнение h ( x ) f ( x ) = h ( x ) g ( x ) при h ( x ) > 0 равносильно совокупности двух систем и

2. В частном случае ( h ( x )= a ) уравнение а f ( x ) = а g ( x ) при а > 0, равносильно совокупности двух систем

и

3. Уравнение а f ( x ) = b , где а > 0, a ≠1, b >0, равносильно уравнению

Решение простейших показательных неравенств основано на свойстве степени. Неравенство вида f ( a x ) > 0 при помощи замены переменной t = a x сводится к решению системы неравенств а затем к решению соответствующих простейших показательных неравенств.

Пример 1 . При каких а уравнение 8 х = имеет только положительные корни?

Решение. По свойству показательной функции с основанием, большим единицы, имеем х>0 8 х >1 >1 >0, откуда a (1,5;4).

Ответ. a (1,5;4).

Решение. Рассмотрим три случая:

§ 7. Логарифмические уравнения и неравенства

Приведем некоторые эквивалентности, используемые при решении логарифмических уравнений и неравенств.

В частности, если а >0, а ≠1, то

log _a g (x)= log _a h(x)

2. Уравнение log _a g (x)=b g (x)= a b ( а >0, a ≠ 1, g(x) >0).

3. Неравенство log _{f ( x )} g ( x ) ≤ log _{f ( x )} h ( x ) равносильно совокупности двух систем: и

Если а, b – числа, а >0, а ≠1, то

log _a f (x) ≤ b

log _a f (x) > b

_{Пример 1. Решите уравнение}

Пример 2. Найдите наибольшее значение а, при котором уравнение

2 log – + a = 0 имеет решения.

При а = квадратное уравнение имеет корень t = >0.

Ответ. а =

Решение. Решим систему неравенств

Корни квадратных трехчленов х _1,2 = 1 ± и х _3,4 = 1 ±.

Критические значения параметра : а = 1 и а = 9.

Пусть Х₁ и Х₂ – множества решений первого и второго неравенств, тогда

Х ₁ Х ₂ = Х – решение исходного неравенства.

Рассмотрим три случая:

3. a ≥ 9 Х – решений нет.

Высокий уровень С1, С2

Пример 1. Найдите все значения р, при которых уравнение

р ∙ ctg 2 x + 2 sinx + p = 3 имеет хотя бы один корень.

Решение. Преобразуем уравнение

При t , E ( f ) = ,

При t , E ( f ) = , то есть при t , E ( f ) = .

Чтобы уравнение 3 t 2 – 2 t 3 = p ( следовательно, и данное) имело хотя бы один корень необходимо и достаточно p E ( f ), то есть p .

Ответ. .

При каких значениях параметра а уравнение log (4 x 2 – 4 a + a 2 +7) = 2 имеет ровно один корень?

Решение. Преобразуем уравнение в равносильное данному:

Отметим, что если некоторое число х является корнем полученного уравнения, то число – х также является корнем этого уравнения. По условию это не выполнимо, поэтому единственным корнем является число 0.

1) a ₁ = 1. Тогда уравнение имеет вид: log (4 x 2 +4) =2. Решаем его

2) a ₂ = 3. Уравнение имеет вид: log (4 x 2 +4) =2 х = 0 – единственный корень.

Высокий уровень С4, С5

Пример 3. Найдите все значения р, при которых уравнение

Пример 4. Найдите все положительные значения параметра а, при которых число 1 принадлежит области определения функции

Если значения х = 1 принадлежит области определения, то должно выполняться неравенство а– а ≥ 0, а≥ а (1)

Таким образом, необходимо найти все а > 0, удовлетворяющие неравенству (1).

1) а = 1 удовлетворяет неравенству (1).

2) При а > 1 неравенство (1) равносильно неравенству 2 + 5а ≥ а 2 +6,

Источник