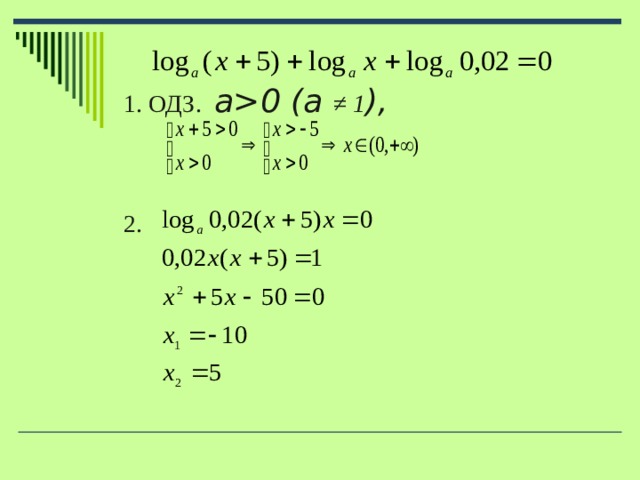Логарифмическое уравнение с параметром и модулем

Занятие по программе элективного курса “Решение логарифмических, показательных уравнений, неравенств с параметрами”

Разделы: Математика

1. Введение

2. Показательные и логарифмические уравнения

Рассмотрим решение показательных и логарифмических уравнений с параметром на конкретных примерах.

Найти все значения параметра a, при которых уравнение 21g(x + 3) = lg ax имеет единственный корень.

Решите следующие примеры самостоятельно.

2. Найти все значения параметра, при каждом из которых уравнение log₃(9 x + 9a 3 ) = x имеет два различных решения.

3. Решите уравнение

.

4. Решите уравнение

.

9. Решите уравнение

.

10. Решите уравнение

.

4. При a ∈ (0; 1) ∪ (1; +∞) x = 3 / 4.

5. При

, при m = 1 x = 1, при

, при m ∈ [-1; 1] x ∈ ∅.

7. При a ∈ (-∞; 1 / 4]

.

9. При

.

3. Показательные и логарифмические неравенства

Решите неравенство

.

При a ≤ 0 и a = 0 показательная функция не определена, следовательно, неравенство не имеет решения.

Рассмотрим решение неравенства при a > 0, a ≠ 1

.

Введем вспомогательную переменную a x = z.

Тогда неравенство принимает вид

или

.

Решив алгебраическое неравенство методом интервалов, получим z ∈ (-∞; 1 / 2) ∪ (1; 2),

или

.

Монотонность показательной функции зависит от величины основания, следовательно,

при a ∈ (0; 1) совокупность неравенств принимает вид

,

а при a ∈ (1; +∞)

.

2. При каких значениях параметра неравенство

верно при любом действительном значении x?

6. Найдите все действительные значения параметра, при которых неравенство 1 + log₂(2x 2 + 2x + 7 / 2) ≥ log₇(cx 2 + c) имеет хотя бы одно решение.

Источник

Логарифмические уравнения, неравенства и системы с параметром

п.1. Примеры

Ответ:
При \(a\leq 1\cup a\gt 100\) решений нет, \(x\in\varnothing\)
При \(a=100\) один корень \(x=1\)
При \(1\lt a\lt 100\) два корня \(x_<1,2>=1\pm\sqrt<1-\frac<\lg a><2>>\)

б) \( x^<\log_a x>=a^2 x \)
ОДЗ: \( \begin x\gt 0\\ a\gt 0\\ a\ne 1 \end \)
Замена: \(t=\log_a x\Rightarrow x=a^t.\) Подставляем: \begin (a^t)^t=a^2\cdot a^t\Rightarrow a^=a^<2+t>\Rightarrow\\ \Rightarrow t^2=2+t\Rightarrow t^2-t-2=0\Rightarrow (t+1)(t-2)=0\Rightarrow \left[ \begin t_1=-1\\ t_2=2 \end \right. \end Возвращаемся к исходной переменной: \begin \left[ \begin \log_a x=-1\\ \log_a x=2 \end \right. \Rightarrow \left[ \begin x_1=a^<-1>=\frac1a\\ x_2=a^2 \end \right. \end Ответ:
При \(0\lt a\lt 1\cup a\gt 1\) два корня \(x_1=\frac1a,\ x_2=a^2\)
При \(a\lt 0\cup a=1\) решений нет.

Пример 2. Решите неравенство:
a) \( \log_a(x-1)+\log_a x\gt 2 \)
\(\log_a(x(x-1))\gt\log_a a^2\) \begin \left[ \begin \begin a\gt 1\\ x-1\gt 0\\ x\gt 0\\ x^2-x\gt a^2 \end \\ \begin 0\lt a\lt 1\\ x-1\gt 0\\ x\gt 0\\ x^2-x\lt a^2 \end \end \right. \Rightarrow \left[ \begin \begin a\gt 1\\ x\gt 1\\ x^2-x-a^2\gt 0 \end \\ \begin 0\lt a\lt 1\\ x-1\gt 0\\ x\gt 1\\ x^2-x-a^2\lt 0 \end \end \right. \end Исследуем параболу \(f(x)=x^2-x-a^2\)
\(D=1+4a^2\gt 0, \forall a\)
\(x_<1,2>=\frac<1\pm\sqrt<1+4a^2>><2>\)
Эта парабола всегда имеет две различных точки пересечения с осью OX.
\(f(x)\gt 0\), при \(x\lt x_1\cup x\gt x_2\)
\(f(x)\lt 0\), при \(x_1\lt x\lt x_2\)
Подставляем в совокупность: \begin \left[ \begin \begin a\gt 1\\ x\gt 1\\ x\lt\frac<1-\sqrt<1+4a^2>><2>\cup x\gt\frac<1+\sqrt<1+4a^2>> <2>\end \\ \begin 0\lt a\lt 1\\ x\gt 1\\ \frac<1-\sqrt<1+4a^2>><2>\lt x\lt \frac<1+\sqrt<1+4a^2>> <2>\end \end \right. \Rightarrow \left[ \begin \begin a\gt 1\\ x\gt \frac<1+\sqrt<1+4a^2>> <2>\end \\ \begin 0\lt a\lt 1\\ a\lt x\lt \frac<1+\sqrt<1+4a^2>> <2>\end \end \right. \end Ответ:
При \(a\gt 1\) луч \(x\in\left(\frac<1+\sqrt<1+4a^2>><2>;+\infty\right)\)
При \(0\lt a\lt 1\) интервал \(x\in\left(1;\frac<1+\sqrt<1+4a^2>><2>\right)\)
При \(a\leq 0\cup a=1\) решений нет.

б) \( \log_x(x-a)\gt 2 \)
\(\log_x(x-a)\gt\log_x x^2\) \begin \left[ \begin \begin x\gt 1\\ x-a\gt x^2\\ x-a\gt 0 \end \\ \begin 0\lt x\lt 1\\ x-a\lt x^2\\ x-a\gt 0 \end \end \right. \Rightarrow \left[ \begin \begin x\gt 1\\ x^2-x+a\lt 0\\ x\gt a \end \\ \begin 0\lt x\lt 1\\ x^2-x+a\gt 0\\ x\gt a \end \end \right. \end Исследуем параболу \(f(x)=x^2-x+a\)
\(D=1-4a\)

в) \( \frac<\log_a(35-x^3)><\log_a(5-x)>\gt 3 \) \begin \frac<\log_a(35-x^3)><\log_a(5-x)>-3\gt 0\\ \frac<\log_a(35-x^3)-3\log_a(5-x)><\log_a(5-x)>\gt 0\\ \left[ \begin \begin \log_a(35-x^3)\gt 3\log_a(5-x)\\ \log_a(5-x)\gt 0 \end \\ \begin \log_a(35-x^3)\lt 3\log_a(5-x)\\ \log_a(5-x)\lt 0 \end \end \right. \Rightarrow \left[ \begin \begin \log_a(35-x^3)\gt \log_a(5-x)^3\\ \log_a(5-x)\gt 0 \end \\ \begin \log_a(35-x^3)\lt \log_a(5-x)^3\\ \log_a(5-x)\lt 0 \end \end \right. \Rightarrow \\ \Rightarrow \left[ \begin \begin a\gt 1\\ \left[ \begin \begin 35-x^3\gt(5-x)^3\gt 0\\ 5-x\gt 1 \end \\ \begin 0\lt 35-x^3\lt(5-x)^3\\ 0\lt 5-x\lt 1 \end \end \right. \end \\ \begin 0\lt a\lt 1\\ \left[ \begin \begin 0\lt 35-x^3\lt(5-x)^3\\ 0\lt 5-x\lt 1 \end \\ \begin 35-x^3\gt (5-x)^3\gt 0\\ 5-x\gt 1 \end \end \right. \end \end \right. \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin \begin 35-x^3\gt(5-x)^3\gt 0\\ 5-x\gt 1 \end \\ \begin 0\lt 35-x^3\lt (5-x)^3\\ 0\lt 5-x\lt 1 \end \end \right. \end \end Решим основное неравенство: \begin 35-x^3\gt(5-x)^3\\ 35-x^3\gt 125-75x+15x^2-x^3\\ 15x^2-75x+90\lt 0\\ x^2-5x+6\lt 0\\ (x-2)(x-3)\lt 0\\ 2\lt x\lt 3 \end Подставляем в систему: \begin \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin \begin 2\lt x\lt 3\\ x\lt 4 \end \\ \begin x\lt 2\cup x\gt 3\\ x\lt\sqrt[3]<35>\\ 4\lt x\lt 5 \end \end \right. \end \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ \left[ \begin 2\lt x\lt 3\\ \varnothing \end \right. \end \Rightarrow \begin 0\lt a\lt 1\cup a\gt 1\\ 2\lt x\lt 3 \end \end Ответ:
При \(0\lt a\lt 1\cup a\gt 1,\ x\in(2;3)\)
При \(a\leq 0\cup a=1\) решений нет

Источник

Методическая разработка для учащихся 11-го класса “Решение логарифмических уравнений с параметром”

Разделы: Математика

Ученик проходит в несколько лет
дорогу, на которую человечество
употребило тысячелетие.
Однако его следует вести к цели
не с завязанными глазами, а
зрячим: он должен воспринимать
истину, не как готовый результат,
а должен её открывать.
Учитель должен руководить этой
экспедицией открытий, следовательно,
также присутствовать не только в качестве простого зрителя.
Но ученик должен напрягать свои силы; ему ничто не должно
доставаться даром. Даётся только тому, кто стремится.

Кто любит учиться, никогда
не проводит время в праздности.

Гений состоит из одного процента вдохновения и девяноста девяти процентов потения.

К сожалению, изучению этих трёх типов решения логарифмических уравнений с параметрами в программе общеобразовательной школы уделяется незаслуженно мало внимания. А подобные уравнения входят в сложную группу заданий, предлагаемых в рамках ЕГЭ, для решения которых необходима хорошая теоретическая подготовка учащихся и уверенное владение технологиями решения математических задач. Выпускник должен не только знать обязательные этапы решения логарифмических уравнений с параметрами, но и хорошо понимать их смысл и назначение, так как многие учащиеся понимают параметр, как «обычное число». Действительно, в некоторых задачах параметр можно считать постоянной величиной, но эта постоянная величина принимает неизвестные значения. Поэтому необходимо рассматривать задачу при всех возможных значениях этой постоянной. В других задачах параметром бывает удобно объявить одну из неизвестных.
На вступительных экзаменах в высшие учебные заведения в виде ЕГЭ встречаются два типа задач с параметрами. Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям». Соответственно и ответы в задачах этих двух типов различаются по существу. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
Основная цель данной методической разработки: научить учащихся решать нестандартные логарифмические уравнения с параметром, показать разные методы их решений, сделать использование этих методов глубоко осмысленными.
Предлагаемые в этой методической разработке методы решения уравнений не сказочный ключ к решению любой задачи. Но они направляют мысль, сокращают время поиска, формируют навыки решения. Все предлагаемые уравнения снабжены подробными решениями. Показано решение 18 уравнений. Но чтобы получить ощутимую пользу от знакомства с готовым решением, необходимо, уловив новую идею, удержаться и не читать дальше, и попробовать затем решать самостоятельно.

При решении логарифмических уравнений с параметрами необходимо придерживаться следующей схемы:

1. Найти область допустимых значений.
2. Решить уравнение (чаще всего выразить х через а).
3. Сделать перебор параметра а с учетом ОДЗ.
4. Проверить, удовлетворяют ли найденные корни уравнения условиям ОДЗ.
5. Записать ответ.

Источник

Проект на тему “Логарифмы с параметрами”

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

муниципальное образовательное учреждение средняя общеобразовательная школа №9

на тему: «Логарифмы с параметрами»

Александрова Светлана Викторовна-учитель математики

Учащийся 11 класса Герасимов Виталий.

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению уравнений, содержащих параметр. Решение задач с параметрами вызывает большие трудности у учащихся, так как их изучение не является отдельной составляющей школьного курса математики, и рассматривается только на немногочисленных факультативных занятиях. Между тем, параметрические уравнения, в том числе и логарифмические, входят в состав сборников ЕГЭ. А ЕГЭ сдавать придется каждому.

Данный проект должен помочь в изучении таких интересных тем, как «Логарифмы» и «Параметры», а так же должен помочь при подготовке к единому государственному экзамену.

Логарифмы, а тем более с параметрами – вещь очень сложная. Поэтому перед началом проекта был проведен опрос в нашем классе (22 человека, 6 не участвовали в опросе) : «Можете ли вы решать логарифмы с параметрами?».

Результаты (представлены в диаграмме) оказались очень интересными:

Как мы видим из результатов опроса, логарифмические уравнения с параметрами особой популярностью не пользуются. Но это и не удивительно: чтобы их решать, нужно знать все о логарифмах.

Решить уравнение, содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения

Виды логарифмических уравнений с параметрами:

Логарифмические уравнения с параметрами можно разделить на три вида в зависимости от местоположения параметра:

Уравнения, содержащие параметры в логарифмируемом выражении.

Уравнения, содержащие параметры в основании.

Уравнения, содержащие параметры и в основании и в логарифмируемом выражении.

Уравнения, содержащие параметры в логарифмируемом выражении:

Уравнения, содержащие параметры в основании:

Из определения логарифма следует, что

Уравнения, содержащие параметры и в основании и в логарифмируемом выражении:

С5. Найдите все значения параметра а, при которых система

имеет ровно два различных решения

Что дал этот проект?

В процессе работы мы овладели начальными навыками решений параметрических уравнений, научились решать логарифмические уравнения с параметрами. Эта работа позволила нам лучше изучить и запомнить все свойства логарифмов. А главное, мы окончательно убедились в том, что есть вещи похуже проектной по технологии.

Результаты повторного опроса:

По окончанию данного проекта был проведен повторный опрос на тему «Можете ли вы решать логарифмические уравнения с параметрами?». Результаты оказались намного лучше предыдущих: теперь все 100% (22 человек) ответили «не могу».

С.И.Колесникова «Решение сложных задач ЕГЭ» 300 задач с подробным решением. Издательство Москва Айрис пресс 2009 год.

Г.А.Воронина Практическое руководство для учителя «Элективные курсы»

Издательство Москва Айрис пресс 2008 год

Ю.Н.Макаров, Н.Г.Миндюк «Дополнительные главы к школьному учебнику»

9-11 класс, Москва Просвещение, 1997г.

КИМы ЕГЭ за 2012-2013 года.

А.Г. Мерзляк и др. «Алгебраический тренажер»., Москва «Илекс», 2005г.

А В Ефремов «Универсальные математические методы», Казань БФ КГТУ, 2010 год.

А.Г. Корянов 2012 задания С ₁ – С ₅ Методы решения (электронный ресурс)

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Номер материала: ДБ-617511

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

Школы организуют экскурсии и спортивные игры в день выборов

Время чтения: 1 минута

Всероссийская олимпиада школьников начнется 13 сентября

Время чтения: 2 минуты

Игры со взрослыми полезнее для развития детей, чем игры со сверстниками

Время чтения: 2 минуты

ЕГЭ в 2022 году может пройти в допандемийном формате

Время чтения: 1 минута

Минобрнауки предлагает дифференцированный подход к аккредитации вузов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Логарифмические уравнения с параметром

Содержимое разработки

Логарифмические уравнения с параметром.

Областью определения его служит решение системы

При a = b мы получим уравнение f(x) = g(x) , равносильное исходному.

При a = b мы получим уравнение f(x) = g(x) , равносильное исходному.

При a ≠ b решение уравнения сводится к решению уравнения

При решении логарифмических уравнений с параметрами необходимо придерживаться следующей схемы:

1. Найти область допустимых значений. 2. Решить уравнение (чаще всего выразить x через a). 3. Сделать перебор параметра a с учетом ОДЗ. 4. Проверить, удовлетворяют ли найденные корни уравнения условиям ОДЗ. 5. Записать ответ.

Типы логарифмических уравнений с параметром:

0 (a ≠ 1 ), 2. ” width=”640″

Источник