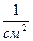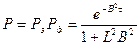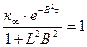Материальный параметр критического реактора сферической формы

Реактор в форме сферы.

Граничными условиями задачи будут конечность плотности потока тепловых нейтронов во всех точках и ее равенство нулю на экстраполированной границе активной зоны.

Решение уравнения (4.23) имеет вид

Из первого граничного условия следует, что постоянная С₂ должна быть равна нулю. Тогда

Из второго граничного условия следует, что

где d— длина линейной экстраполяции.

Так как С), /?₀ и d отличны от нуля, то sin B(R₀ + d) = 0, следовательно, B(Rq + d) = пп, где n — любое целое число.

Распределение плотности нейтронного потока по радиусу сферического реактора имеет вид

Как было отмечено, С] определяется по заданной мощности реактора.

Тогда мощность реактора может быть выражена через число делений следующим образом:

Использовав соотношение (4.26) и выразив элементарный объем через сферические координаты, после интегрирования получим

Как видно из (4.26), распределение плотности нейтронного потока по радиусу активной зоны неравномерно. Количественной характеристикой степени неравномерности является коэффициент неравномерности плотности потока нейтронов, представляющий собой отношение максимальной плотности потока нейтронов к средней:

Если считать для упрощения экстраполированные размеры активной зоны равными физическим, будем иметь

Реактор в форме цилиндра. Энергетические ядерные реакторы, как правило, имеют цилиндрическую форму.

Рис. 4.3. Схема цилиндрического реактора

Рассмотрим реактор радиусом Я и высотой Н (рис. 4.3). Под размерами Я и Я в дальнейшем будем понимать действительные размеры, увеличенные на длину линейной экстраполяции.

Распределение плотности потока тепловых нейтронов в реакторе по-прежнему описывается волновым уравнением, которое для цилиндрических координат имеет вид

Решение уравнения (4.27) будем искать методом разделения переменных, полагая

После подстановки (4.28) в (4.27) получим Разделив все члены уравнения на 02, будем иметь

В уравнении (4.29) первый член зависит только от /-, а второй — только от И. Поэтому каждый из них можно положить равным некоторой постоянной величине. Пусть

Таким образом, получим, что где а“ и Р“ — произвольные постоянные.

Уравнение (4.30) может быть сведено к уравнению Бесселя. Введем новую независимую переменную и = а г; так как а —

величина постоянная, то

Выразим производные 0 по г через новую независимую переменную:

После подстановки в уравнение (4.30) получим или

Уравнение (4.32) при положительном значении и, а следовательно, и а

есть уравнение Бесселя нулевого порядка, общее решение которого имеет вид

где У₀ и Т₀ — функции Бесселя нулевого порядка соответственно первого и второго рода.

На рис. 4.4 приведены графики функции Бесселя. Имея в виду граничные условия, приходим к выводу, что второе слагаемое в уравнении (4.33) должно быть равно нулю, так как при стремлении аргумента к нулю значение функции нулевого порядка второго рода стремится к бесконечности. Следовательно,

Теперь определим значение а. Плотность нейтронного потока на экстраполированной границе равна нулю: Ф(/?, И) = 0 (при г = /?), а так как нейтронный поток равен нулю по всей высоте реактора при г = /?, то

Постоянная интегрирования А не может быть равна нулю, так как теряет смысл само решение. Значит,

Наименьшее собственное значение а“ соответствует решению при минимальном аргументе и равно первому корню функции Бесселя 7₀(и) = 0. Из графика на рис. 4.4, а следует

Для определения р вернемся к функции 2 <И).Из равенства (4.31) следует

Решение уравнения (4.36), отвечающее граничным условиям, запишется в виде

Постоянная интегрирования не может быть равной нулю. Следовательно, при Значит, , откуда

Изменение плотности нейтронного потока по высоте реактора будет определяться как

Значение плотности нейтронного потока в любой точке активной зоны реактора может быть найдено по выражению

Геометрический параметр цилиндрического реактора конечных размеров

Коэффициент неравномерности распределения плотности нейтронного потока по высоте активной зоны определяется следующим образом:

Коэффициент неравномерности распределения плотности нейтронного потока по радиусу активной зоны

Произведением коэффициентов К_ь и К,, оценивается неравномерность распределения плотности нейтронного потока по объему активной зоны:

В заключение следует отметить, что для активной зоны в форме параллелепипеда с размерами ребер а, Ь и с аналогичным способом можно получить:

Источник

Уравнение критичности для реактора конечных размеров.

Значение величин λ, υ, μ, φ, Θ, r позволяет определить к_∞(коэффициент размножения в бесконечной среде). Для реактора конечных размеров к_{эфф 2 )-геометрический параметр, который зависит от формы и размеров активной зоны. Для}

сферы с R: ,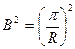

цилиндра R и Н: ,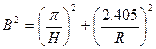

Для бесконечной среды к_∞=1,для реактора конечных размеров к_эфф=1,что является условием критичности для реактора конечных размеров

Утечка нейтронов зависит от отношения поверхности активной зоны к ее объему. Поэтому наименьшая критическая масса для активной зоны определенного объема и определенного состава имеет место при наименьшем значении поверхности активной зоны.

Зная наивыгоднейшее соотношение между размерами, можно найти зависимость минимального критического объема от величины материального параметра, равного в критическом реакторе геометрическому параметру.

Для цилиндрической активной зоны:

,

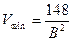
Для сферы 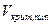наименьшее, так как сфера имеет наименьшую поверхность.

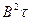
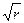
Уравнение критичности может быть значительно упрощено для случая больших реакторов. Большими считаются реакторы, для которых ‹‹1, то есть ‹‹1 или R›› .

Отсюда видно, что большими реакторами являются такие, у которых размеры активной зоны намного больше длины замедления.

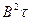
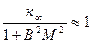
Тогда при удовлетворении неравенства ‹‹1 получим

, где М 2 = L 2 + r –площадь миграции.

Кроме определения критических размеров важное практическое значение имеет и другая задача- расчет эффективного коэффициента для активной зоны определенных состава, формы и размеров. Для этого используют уравнение

,

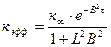
в которое с этой целью вместо В 2 подставляется рассчитанное для данного реактора значение геометрического параметра.

В расчетах реакторов встречается и обратная задача- определение размеров активной зоны определенного состава и геометрической формы, которые обеспечивают необходимое значение к_эфф, найденное из условия обеспечения заданной продолжительности работы реактора. Для этого из уравнения к_эфф при выбранном значении к_эфф находят материальный параметр В 2 и приравнивают его к геометрическому параметру. Из этого последнего уравнения и определяются требуемые размеры активной зоны.

Уравнение критичности позволяет обнаружить зависимость критических размеров активно зоны от площади миграции. Из этого уравнения следует, что с увеличением L и τ материальный параметр уменьшается и следовательно, уменьшается равный ему геометрический параметр. А это означает, что критические размеры реактора возрастают. Данный результат физически вполне очевиден.

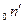
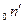
Действительно τ характеризует расстояние по прямой, на которое смещается в процессе своего замедления до тепловой энергии, а L 2 характеризует расстояние, пройденное тепловым до точки захвата. Чем больше эти расстояния, тем меньше вероятность того, что нейтрон избежит утечки в процессе диффузии и замедления, то есть тем больше размеры реактора, при которых протекает самоподдерживающаяся цепная реакция.

Например, реактор, где в качестве замедлителя- вода при прочих равных условиях будет иметь гораздо меньше размеры, чем реактор с графитовым замедлителем, так как для воды L=2,72см, τ= 31см, а для графита L=58см, τ= 313см. Вследствие высокого содержания Н₂ органические жидкости приближаются к воде по замедляющим и диффузионным качествам. Поэтому реактор с органическим замедлителем имеют малые габариты.

Дата добавления: 2015-06-17 ; просмотров: 3404 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Основы построения реактора

Глава 6. Основы работы атомных электростанций

Понятие о цепной реакции

Известно, что при бомбардировке атомов урана–235 в результате его деления из осколков вылетает 2 – 3 новых нейтрона способных производить дальнейшее деление соседних атомов. Однако этот процесс деления следующих атомов нейтронами возможен только при достаточном и определенном количестве урана-235. Процесс лавинообразного нарастания деления последующих атомов урана-235 называется цепной реакцией деления ядер.

Выделение энергии при ядерных реакциях соответствует принципу Эйнштейна:

,

где — изменение массы системы, кг;

— соответствующее ему изменение энергии, Дж;

Любой химический элемент М символически обозначается как , где z – число протонов в ядре атома; А – массовое число равное сумме чисел протонов и нейтронов в ядре. Например, соответствует изотопу урана, в ядре которого 92 протона и 143 нейтрона, а их сумма равна 235.

Выделение энергии при делении ядра урана определяется из уравнения:

,

где La – лантан; Br – бром; Q – тепловая энергия реакции, Дж.

Тепловая энергия ядерной реакции определяется по уравнению:

,

М(М А ) – молярная масса вещества.

После подстановки массы элементов, участвующих в реакции получим Q = 193 МэВ.

При делении ядер, содержащихся в 1 г урана-235, выделяется энергия 7,8·10 10 Дж, т.е. 1 г урана-235 эквивалентен более чем 2 т. высококалорийного угля.

При делении ядер тепловыми нейтронами, находящимися в равновесии с ядрами вещества среды, выделяется в среднем следующее количество вторичных нейтронов: п = 2,58 для ; п = 2,47 для ; п = 3,5 для (плутоний).

Кроме мгновенно выделяющихся нейтронов имеются запаздывающие нейтроны, наличие которых обеспечивает управление цепной реакцией деления ядер. На долю запаздывающих нейтронов приходится около 0,7 % общего числа нейтронов. При столкновении нейтронов с ядрами его энергия уменьшается. После ряда столкновений скорость нейтрона уменьшается до значения, соответствующего скорости теплового движения ядер вещества. Таким образом, нейтрон достигает тепловой энергии (становится тепловым нейтроном). Например, при Т = 300 К скорость движения теплового нейтрона равна 2200 м/с. В соответствии с этим реакторы АЭС подразделяются на тепловые и быстрые.

Процесс деления ядер обычно представляется на основе капельной модели ядра, согласно которой реакция взаимодействия его с нейтроном имеет две стадии. В первой стадии, частица поглощается ядром, в результате чего образуется возбужденное ядро. Во второй стадии, возбужденное ядро приходит либо в стабильное состояние, испуская элементарную частицу или квант, либо делится. На этот процесс большое влияние оказывают энергия связи и энергия порога деления.

Энергия связи – энергия, вносимая нейтроном в ядро и достаточная, чтобы войти в него и удержаться в нем:

.

Энергия порога деления – энергия достаточная, для того чтобы ядро атома начало делиться. Для того чтобы ядро разделилось необходимо к нему подвести энергию не ниже энергии порога деления (Е_п.д). Для сравнения в табл.6.1. даны эти энергии для урана-235 и урана-239.

Энергетические характеристики урана

Наименование элемента	Энергия порога деления, Еп.д МэВ	Энергия связи, Еп, МэВ
Уран-236,	5,75	6,4
Уран-239,	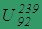5,85	4,76

Сравнивая, видно, что при захвате теплового нейтрона ураном-235, ядро 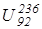получает энергию возбуждения большую порога деления этого ядра, поэтому ядро урана-236 готово делиться, и наоборот, уран-238 при попадании в него нейтрона получает энергии возбуждения (Е_п.д) меньше, поэтому оно не делится.

Характеристикой взаимодействия нейтронов с ядром вещества является вероятность этого события (встречи или столкновения). Вероятность ядерной реакции одного нейтрона с N количеством ядер, находящихся в единице объема вещества называется макроскопическим сечением:

Тип ядерной реакции определяется соответствующим макроскопическим сечением:

— Σ_а = σ_а N – макроскопическое эффективное сечение поглощения;

— Σ_f = σ_f N – макроскопическое эффективное сечение деления;

— Σ_s = σ_s N – макроскопическое эффективное сечение рассеивания.

Величина Σ_f зависит от энергии нейтронов. Например, для быстрых нейтронов урана-235 с энергией 2 МэВ σ_f = 0,5 б, тогда как для тепловых нейтронов урана-235 с энергией 0,025 МэВ σ_f =590 б. Поэтому в реакторах, в которых нейтроны находятся в тепловом равновесии с ядрами урана-235, деление происходит с наибольшей вероятностью.

Поскольку при одном акте деления ядра урана образуется несколько нейтронов, то цепная реакция деления в уране-235 вполне возможна. Однако в природном уране основным изотопом является уран-238 (его в природе до 99,3 %), а на долю урана-235 приходится всего 0,7 %, поэтому цепная реакция в природном уране не развивается, нейтроны поглощаются ядрами урана-238.

Самоподдерживающаяся цепная реакция деления в смеси изотопов урана создается путем увеличения содержания изотопов урана-235 в смеси и применение замедлителя нейтронов. Замедление нейтронов деления достигается при столкновении их с легкими ядрами замедлителя, введенного в урановую среду. Захват нейтронов легкими ядрами маловероятен, так как масса его ядра близка к массе нейтрона и, таким образом, происходит обмен упругими ударами между ними. В замедлителе нейтрон теряет свою кинетическую энергию до теплового состояния, после чего блуждает в среде до поглощения его ядрами урана-235 с последующим делением.

Отношение числа нейтронов какого-либо поколения к числу нейтронов предшествующего поколения называется коэффициентом размножения k.

Если k >1, то количество нейтронов возрастает.

Если k = 1, то количество нейтронов остается неизменным, а реакция деления происходит с постоянной скоростью.

.

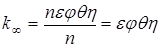
v – скорость нейтронов, см/с.

Среднее расстояние λ, проходимое нейтронами между взаимодействиями с соседними ядрами вещества обратно пропорционально макроскопическому эффективному сечению: λ = 1/Σ.

Количество взаимодействий нейтронов, находящихся в единице объема, за единицу времени, 1/(с см 3 ) определится по уравнению

.

В единице вещества нейтронного потока Ф в единицу времени происходит Σ_аФ поглощений, Σ_fФ делений и Σ_sФ актов рассеивания.

Основное уравнение реактора выражает зависимость эффективного коэффициента размножения нейтронов от состава и размеров активной зоны:

,

где — материальный параметр, зависящий от свойств материалов активной зоны; для критического состояния реактора материальный параметр становится равен геометрическому;

D – коэффициент диффузии нейтронов;

τ – возврат нейтронов, зависящий от квадрата среднего расстояния, проходимого нейтроном в процессе замедления;

L – длина диффузии нейтронов.

Параметр В отражает также размеры и геометрическую форму активной зоны. В этом случае величина В называется геометрическим параметром и для цилиндрической активной зоны она определяется по уравнению

,

где R – радиус активной зоны, м;

Н – высота активной зоны, м (расчетная длина ТВЭЛ).

Таким образом, из последних двух уравнений можно определять размеры активной зоны, если известен ее состав. Оптимальным соотношением между высотой и радиусом активной зоны является Н/R ≈ 1,85.

Распределение нейтронного потока по объему активной зоны для цилиндрической формы определяется уравнением:

,

где — значение нейтронного потока в центре активной зоны;

— текущее значение функции Бесселя;

Утечка нейтронов через поверхность активной зоны снижает плотность нейтронов во всех ее частях, создавая неравномерность распределения нейтронного потока. В реакторах без отражателей максимальное значение потока тепловых нейтронов соответствует геометрическому центру активной зоны, уменьшаясь к ее границам.

Коэффициент неравномерности нейтронного потока определяется по выражению

.

Наибольшее значение нейтронного потока ( ) имеет место при r = 0. В этом случае изменение нейтронного потока по высоте реактора определяется соотношением:

.

В этом случае изменение Ф по радиусу описывается уравнением

.

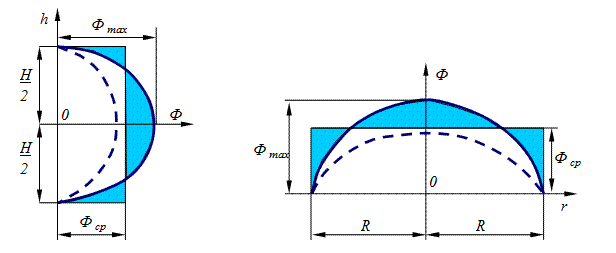
Значения нейтронного потока в активной зоне реактора в различных точках по высоте и радиусу показаны на рис.6.2. Штриховые линии означают изменение нейтронного потока Ф по высоте и радиусу при r ≠ 0 и h ≠ 0.

Рис.6.2. Изменение нейтронного потока по высоте и радиусу активной

Неравномерность нейтронного потока по объему активной зоны оценивается произведением коэффициентов неравномерностей по высоте k_h и радиусу k_r:

.

В энергетических реакторах обычно Ф_ср = 10 12 ÷ 10 14 1/(с см 2 ).

Для уменьшения утечек нейтронов активную зону реактора окружают отражателем 4 (рис.6.1), от которого нейтроны попадают обратно в активную зону, что улучшает баланс нейтронов в реакторе. За счет этой экономии нейтронов можно либо уменьшить размеры активной зоны без изменения ее состава, либо уменьшить обогащение ядерного горючего при неизменных размерах активной зоны.

При утечке из активной зоны быстрых нейтронов они замедляются в отражателе и возвращаются в активную зону уже тепловыми. Поэтому поток тепловых нейтронов вблизи границы активной зоны реактора увеличивается.

Зная средний поток нейтронов, можно определить тепловую мощность реактора:

,

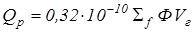
Среднее удельное объемное тепловыделение ядерного горючего определяется по уравнению

.

Средние коэффициенты неравномерности тепловыделения равны средним коэффициентам неравномерностей нейтронного потока активной зоны реактора: k_r = 2,31; k_h = 1,57; k_v = k_r k_h = 2,31·1,57 = 3,67. Таким образом, максимальное удельное объемное тепловыделение равно:

.

При проектировании реакторов снижение неравномерности тепловыделения является одной из основных задач, так как это мероприятие повышает мощность реактора, увеличивает глубину и равномерность выгорания ядерного топлива, увеличивает компанию реактора.

Источник