Местная ось х1 направлена вниз для вертикальных стержней как исправить

Местные системы координат стержня

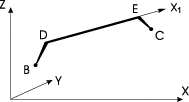
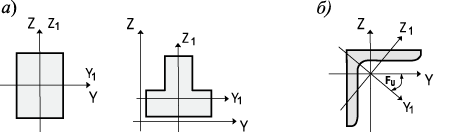
Стержневой конечный элемент универсального вида изображен на рис. 1. На его концах могут быть абсолютно жесткие (недеформируемые) вставки BD и CE. Узел B является началом стержня, узел C — его концом. Для упругой части стержня DE принято следующее обозначение концевых сечений: номером 1 обозначается сечение у начала стержня, номером 2 — у его конца.

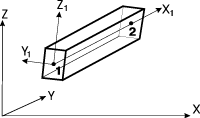
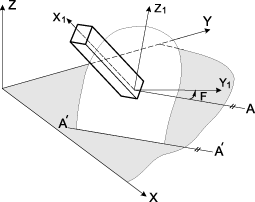
В общем случае предполагается, что стержень может быть произвольным образом расположен по отношению к принятой общей системе координат XYZ. Однако характеристики отдельно взятого конечного элемента стержневого типа удобнее получать в системе координат, опре­деленным образом связанной с данным элементом. Для этого на упругой части, изображенной на рис. 2, определена местная система координат X₁Y₁Z₁ (В SCAD используются только правые системы координат. Система координат считается правой, если ось Y образуется поворотом оси X против часовой стрелки при взгляде с конца оси Z на угол 90°), относительно которой вычисляются усилия и задаются некоторые исходные данные. В этой системе оси Y₁ и Z₁ являются главными осями инерции поперечного сечения.

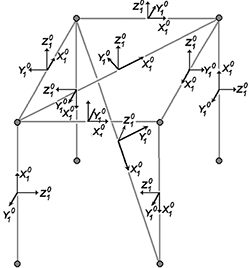
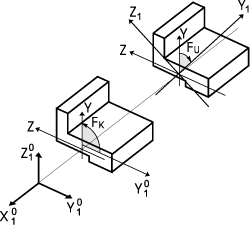
Однако еще до ввода информации о форме поперечного сечения система SCAD строит оси («пре­дварительный проект») локальной системы координат X₁ 0 Y₁ 0 Z₁ 0 (рис. 3, а) с использованием следующих соображений:

Это угол между осью Y₁ и прямой, связанной с глобальной системой координат. В качестве такой прямой принимается линия пересечения плоскости, параллельной XОY, и плоскости поперечного сечения стержня Y₁OZ₁, проходящей через начало упругой части стержня (рис. 5). Эта прямая (ось А) ориентирована так, чтобы тройка X₁AZ₁ была правой. При этом считается, что оси X₁Y₁Z₁ образуют правую тройку, а ось Z₁ всегда направлена в верхнее полупространство (в сторону возрастания координаты Z).

Положительное значение угла ориента­ции F_K определяется поворотом оси А до ее со­вмещения с осью Y₁ против часовой стрелки, если смотреть с конца оси X₁.

Окончательно положение главных осей инерции поперечного сечения определяется значением суммы «угла разворота конструктивных осей FK» между конструктивной осью Y(Z) и осью Y 0 ₁(Z 0 ₁) с углом наклона главных осей инерции к конструктивным осям сечения FU (рис. 6). При назначении сечений из сортамента металлопроката или же при использовании для этого программ Конструктор сечений, Тонус и Консул учет угла F_U выполняется системой автоматически.

Положительное значение углов F_K (F_U) определяется поворотом сечения против часовой стрелки, если смотреть с конца оси X₁. Таким образом, на рис. 6 угол F_K является положительным, а угол F_U — отрицательным.

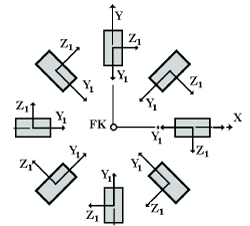
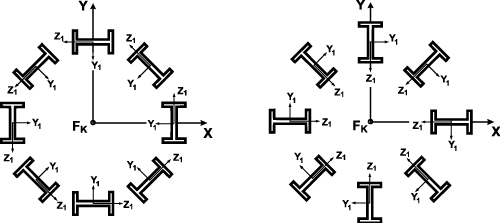
Более удобным способом задания положения локальных осей по отношению к глобальным координатам является за­да­ние некоторой дополнительной точки (точка ориентации), ко­торая должна иметь положительную координату Y₁ или Z₁ (см. ниже). Так для всех вер­ти­кальных колонн цилинд­ри­чес­кого сооружения (рис. 7) задается одна и та же точка ори­ен­та­ции F_K с координатами центра круга сооружения (пред­полагается, что глобальные оси проведены через этот центр).

Для того чтобы расположить стержень в пространстве вполне определенным способом, следует указать, какой имен­но угол используется — с конструктивными или с главными осями инерции. При этом можно задать, какая именно из осей Y₁ или Z₁ (аналогично y или z) направлена в сторону точки ориентации. Естественно, что результат при этом меняется (рис. 8).

Следует, однако, помнить, что при использовании сечений, у которых не равен нулю угол F_U, может оказаться, что схема типа «плоская рама» некорректна. Это связано с тем, что главные оси инерции стержня не лежат в выбранной силовой плоскости. При контроле исходных данных такие ошибки идентифицируются. Эта ситуация, казалось бы, не должна иметь место при расчете конструкций, где в составе системы стержни работают только на растяжение/сжатие (элементы типа 1 или 4). Но поскольку в SCAD и для таких случаев предусмотрена, например, местная нагрузка по направлениям главных осей инерции, то она может уже не действовать в плоскости рамы. Поэтому запрет сохраняется и в этом случае.

Источник

Согласование осей стержней

Перед согласованием (сонаправлением) местных осей Y1 и Z1 (которые задают поворот поперечного сечения стержня), нужно проконтролировать направление продольной местной оси X1.

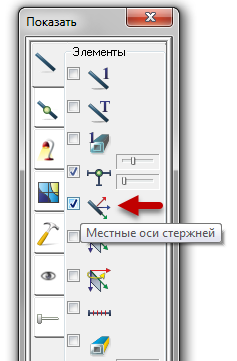
Для визуализации местных осей стержней во флагах рисования во вкладке «Элементы» нужно включить соответствующую галочку:

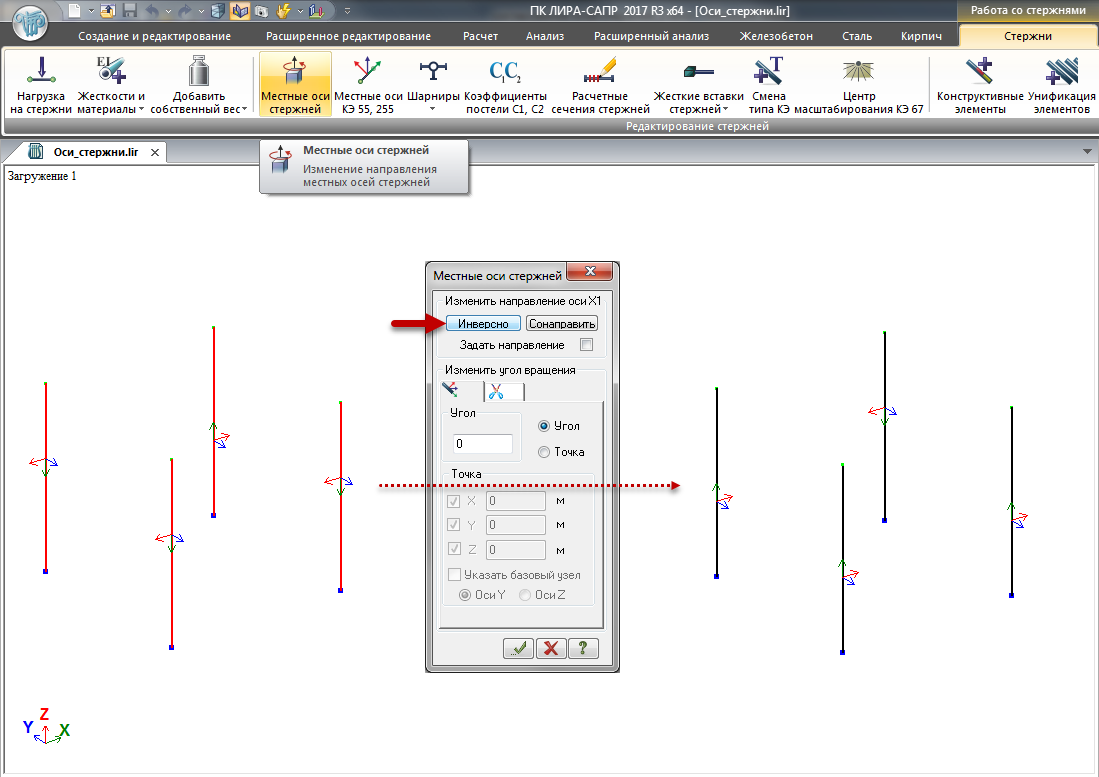
Для изменения направления оси Х1 стержня необходимо отметить соответствующие элементы, перейти в появившуюся контекстную вкладку «Стержни» → «Местные оси стержней».

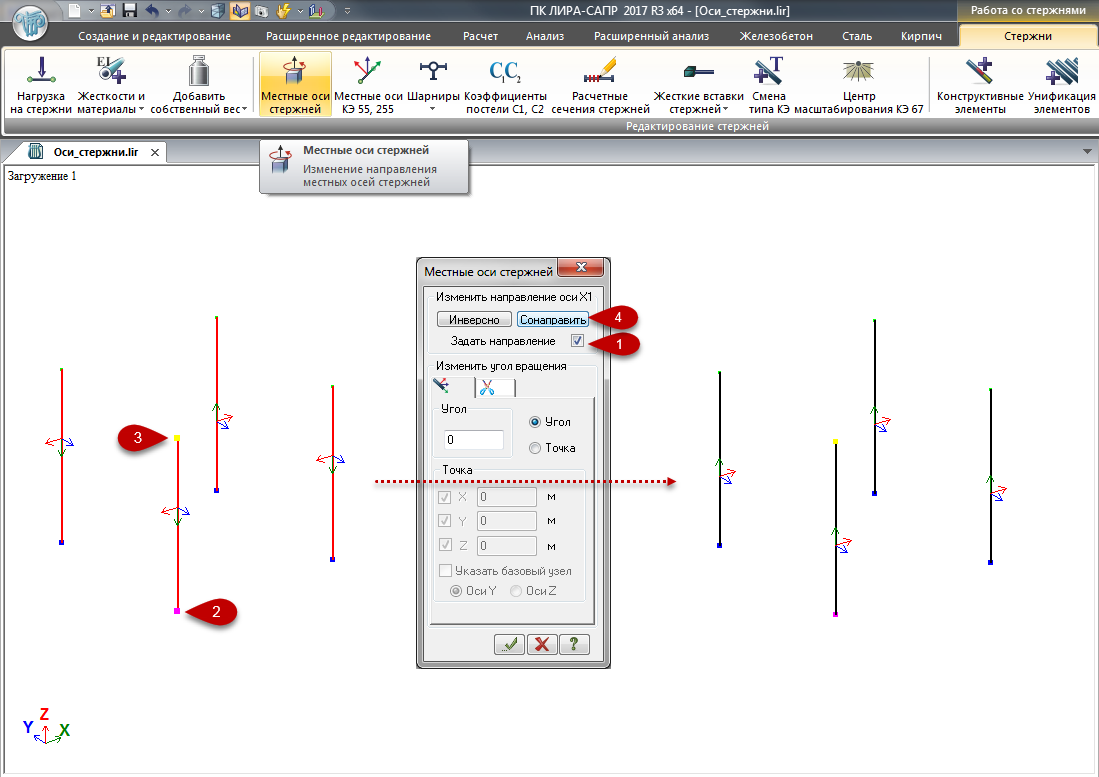
При нажатии «Сонаправить» произойдет разворот осей Х1 в выделенных параллельных стержнях в ту сторону, куда направлены оси Х1 большинства выделенных элементов. Если предварительно нажать галку «Задать направление» и парой узлов (первый – розовый, второй – желтый) указать на схеме в какую сторону развернуть оси Х1, то сонаправление произойдёт в указанном направлении.

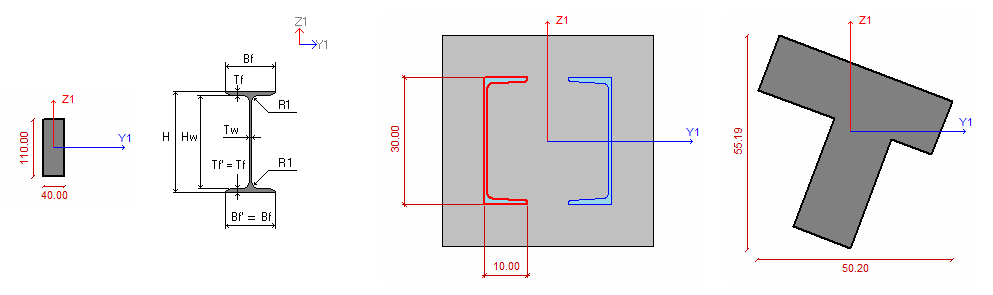
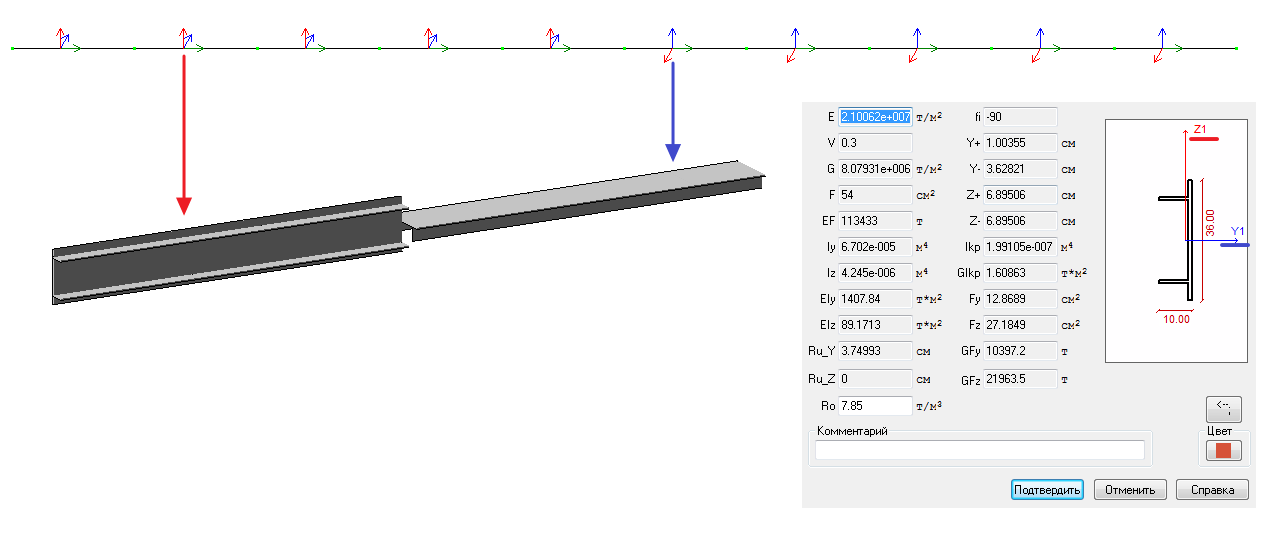
Усилия в стержневых элементах определяются относительно местных осей, так момент Му действует в плоскости вокруг оси Y1 (т.е. в плоскости местных осей Х1Z1), а момент Mz вокруг оси Z1. Каким образом местные оси стержня соотносятся с заданным сечением, можно увидеть в меню «Жесткости» для каждого из возможных сечений: стандартное, стальное, сталежелезобетонное, из конструктора сечений.

Причем для стальных сечений в диалоге задания можно развернуть сечение относительно показанных осей Y1-Z1 на угол с шагом 90 градусов, а для остальных сечений нет такой опции.

Для численно заданных жесткостей характеристики назначаются сразу относительно местных осей стержня, это нужно помнить, задавая параметры жесткостей.

При необходимости задать нужную ориентацию сечения элемента, т.е. развернуть местные оси элемента, можно разными способами:

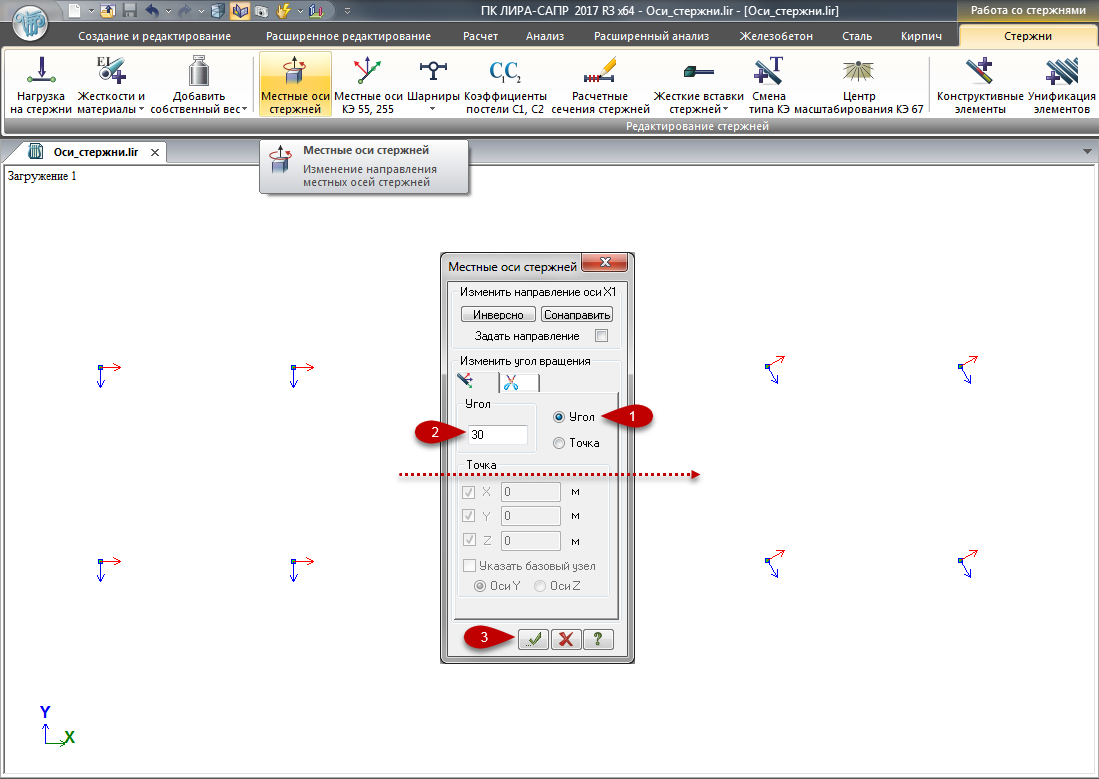
1. поворот на заданный угол относительно первоначального положения (именно относительно первоначального положения, а не положения предшествующего повороту)

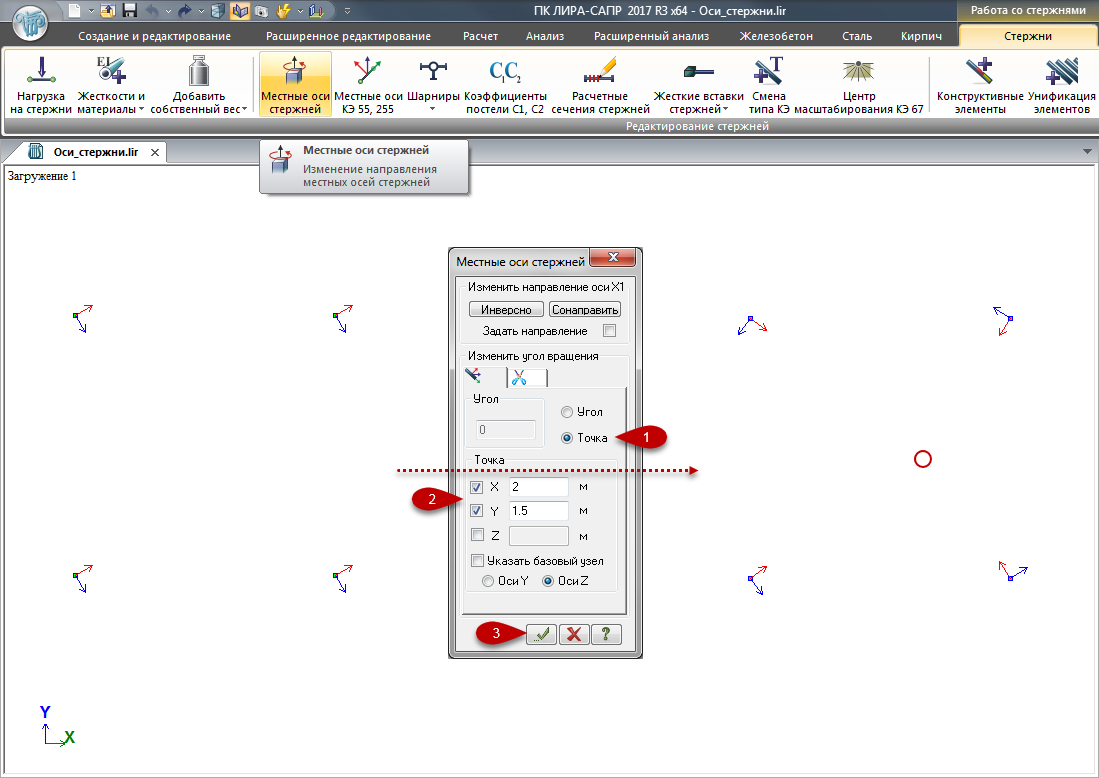
2. поворот на указанную точку

Можно задавать не все координаты этой точки – незаданные координаты будут приняты такими же, как центр тяжести у самого стержня, таким образом, для каждого стержня эта координата будет своя.

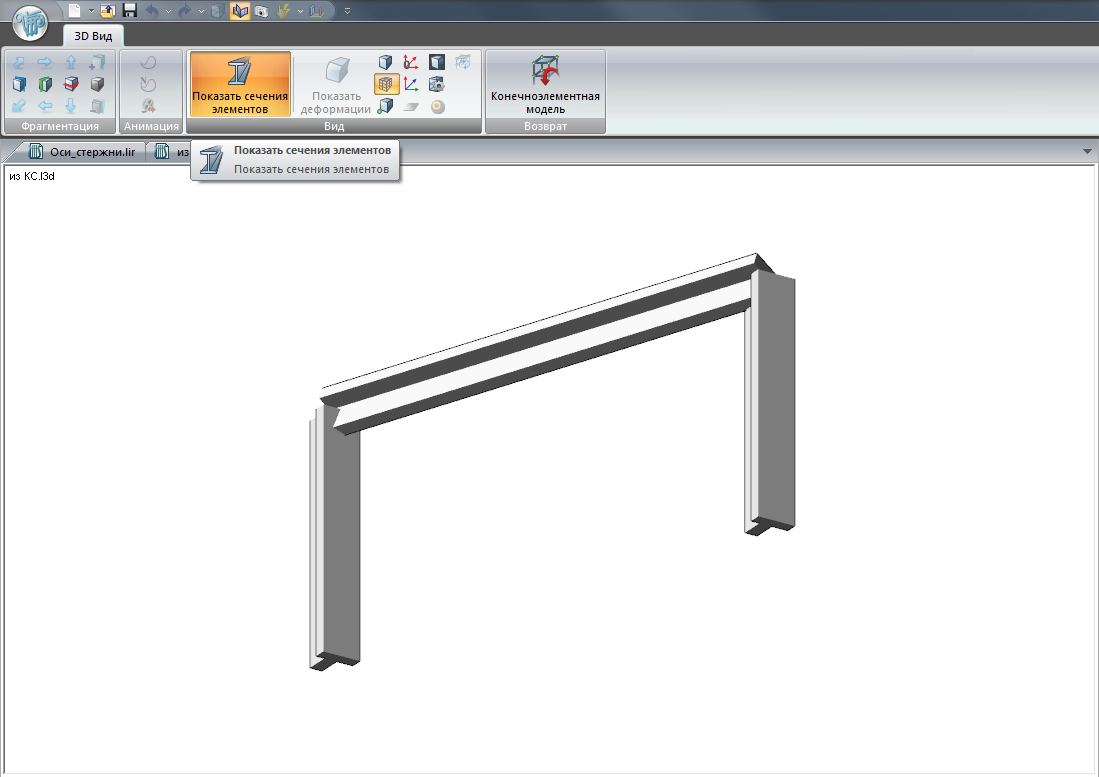
Корректность положения/поворота сечения элемента в схеме можно проверить в 3D-виде:

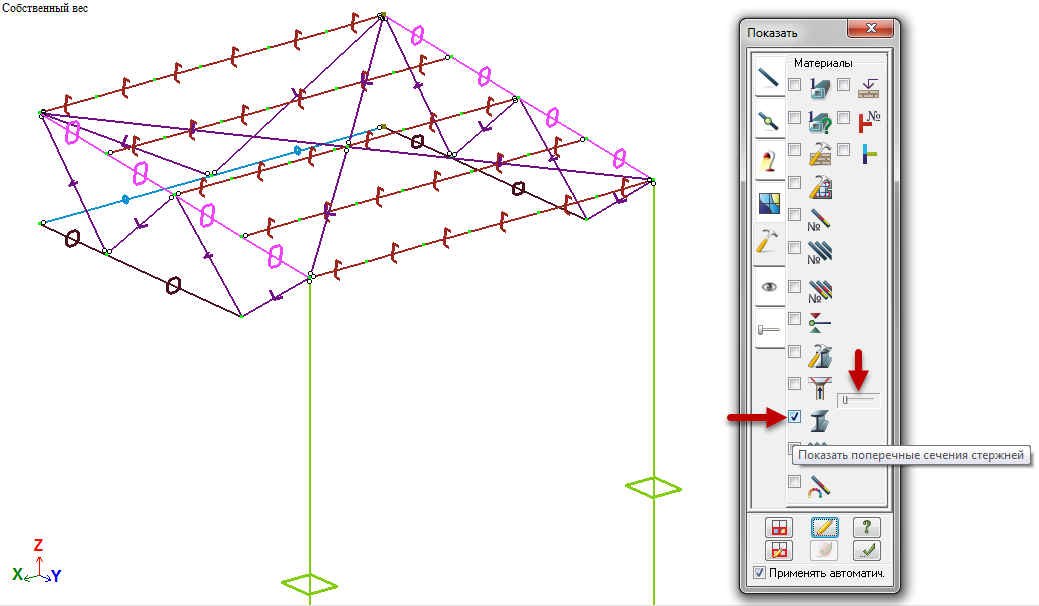
Или включить во флагах рисования во вкладке «Материалы» галочку «Показать поперечные сечения стержней». Рядом есть ползунок для регулировки масштаба отрисованного сечения.

Примеры некорректно заданных поворотов сечений и их исправление:
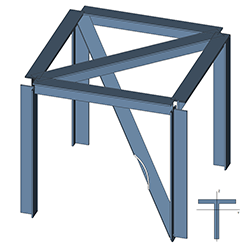
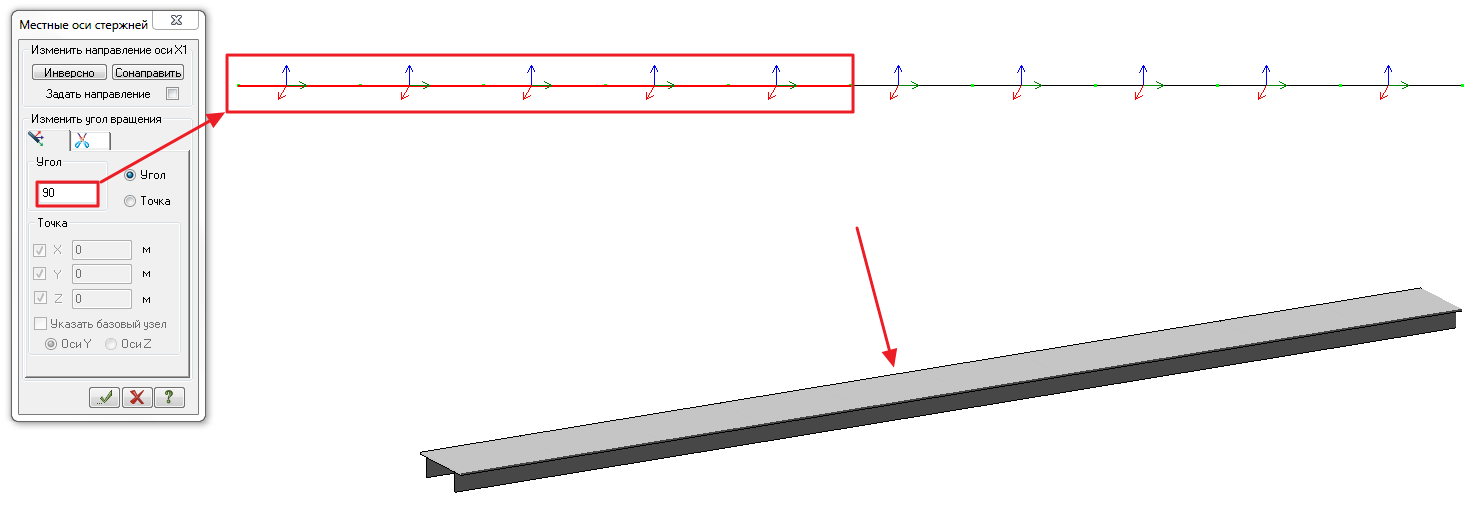
Для корректной ориентации сечения по длине стержня следует контролировать их местные оси. Так, ось Z1 для сечения на рисунке ниже лежит в плоскости полки, ось Y1 – в плоскости стенки. Для левой части балки ось Z1 вертикальная, ось Y1 – горизонтальная. Для правой наоборот.

Для того чтобы полка балки лежала в горизонтальной плоскости следует развернуть местные оси:

Или, чтобы не выделять курсором вручную все элементы повернутые «не так», можно было направить ось Z1 в точку с координатой Y= 10000 м, а оси X и Z выключить (считаем, что балка направлена вдоль глобальной оси Х, т.е. ось Y поперек балки), как в примере ниже.

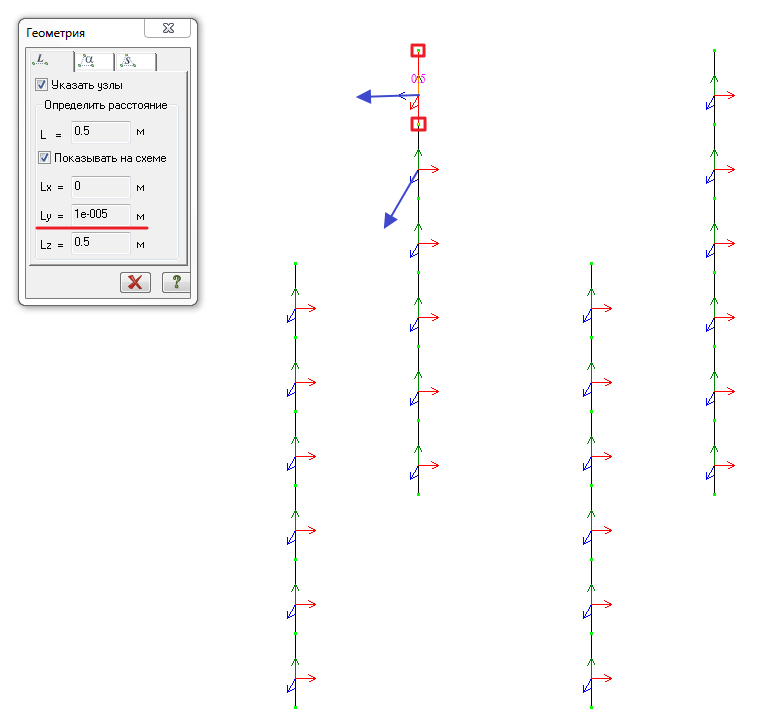
Также следует следить за ориентацией осей элементов, узлы которых не лежат в ортогональных плоскостях. Например, колонны, немного отклонённые от вертикали. На рисунке ниже между отмеченными узлами по оси Y расстояние 0.0001 м. Поэтому местные оси Z1 направлены в разные стороны (программа считает элементы уже наклонными, и разворачивает местную ось Z1 в верхнее полупространство).

Для сонаправления осей следует указать, что местная ось Z1 должна смотреть в точку с координатой Х = 10000 м, а остальные оси выключить (таким образом, оси Z1 всех выделенных стержней направятся в точку с координатами Х = 10000 м и координатами Y и Z, как у центров самих стержней):

Источник

Направление расположения арматуры в SCAD

proekt прав. А про выровнять оси. Ну видимо это не нужно, раз нет такой функции. В схемах присутствуют и треугольники и ромбы, как там “оси лягут”, кто их знает

A III, вот это я зажёг!
По-моему, вы путаете понятие местных осей элемента и осей выдачи напряжений. На приведенном примере оси как были на своих местах, так и остались. И чего тут путаться?

Из справки к СКАДу:

· назначить направление оси Х вычисления напряжений в общей системе координат. При этом заданная ось проектируется на плоскость элемента, а ось Y лежит в плоскости элемента и проходит перпендикулярно полученной проекции;

· назначить точку. Проекция линии на плоскость элемента, соединяющая эту точку с первым узлом элемента, определяет ось Х вычисления напряжений, а ось Y лежит в плоскости элемента и проходит перпендикулярно полученной проекции.

Ось Х выдачи напряжений может быть задана приращениями относительно первого узла элемента, координатами точки, или явным указанием оси общей системы координат.

После активизации опции и задания в диалоговом окне необходимых данных следует выбрать на схеме элементы, для которых применяются сделанные назначения, и нажать кнопку ОК в разделе Назначения.

Для отмены сделанных назначений необходимо установить режим задания осей и нажать в диалоговом окне кнопку Отменить выравнивание. После выхода из окна выбрать на схеме элементы, у которых направление осей выдачи напряжений должно совпадать с направлением местных осей, и нажать кнопку ОК.

Источник

Направление расположения арматуры в SCAD

proekt прав. А про выровнять оси. Ну видимо это не нужно, раз нет такой функции. В схемах присутствуют и треугольники и ромбы, как там “оси лягут”, кто их знает

A III, вот это я зажёг!
По-моему, вы путаете понятие местных осей элемента и осей выдачи напряжений. На приведенном примере оси как были на своих местах, так и остались. И чего тут путаться?

Из справки к СКАДу:

· назначить направление оси Х вычисления напряжений в общей системе координат. При этом заданная ось проектируется на плоскость элемента, а ось Y лежит в плоскости элемента и проходит перпендикулярно полученной проекции;

· назначить точку. Проекция линии на плоскость элемента, соединяющая эту точку с первым узлом элемента, определяет ось Х вычисления напряжений, а ось Y лежит в плоскости элемента и проходит перпендикулярно полученной проекции.

Ось Х выдачи напряжений может быть задана приращениями относительно первого узла элемента, координатами точки, или явным указанием оси общей системы координат.

После активизации опции и задания в диалоговом окне необходимых данных следует выбрать на схеме элементы, для которых применяются сделанные назначения, и нажать кнопку ОК в разделе Назначения.

Для отмены сделанных назначений необходимо установить режим задания осей и нажать в диалоговом окне кнопку Отменить выравнивание. После выхода из окна выбрать на схеме элементы, у которых направление осей выдачи напряжений должно совпадать с направлением местных осей, и нажать кнопку ОК.

Источник

Как не наделать ошибок с осями пластин при расчете в Лире. Видеоурок.

Для тех, кто торопится: внизу статьи есть видео по теме ↓. Но сначала, как всегда, “немного” текста с иллюстрациями.

В Лире есть такая возможность – построить самому объекты любой конфигурации и любой сложности с нуля. Собрать свой лего из палочек и пластинок. Вот только иногда из-за незнания особенностей построения можно получить очень странные результаты. И хорошо, если вы имеете представление о работе конструкции и знаете, где должна быть расположена рабочая арматура. А если нет? Если опыт расчетов невелик и вы доверяете результатам программы? Тогда будьте готовы заармировать все с точностью до наоборот.

На рисунке выше вы видите изгибающие моменты в двух практически одинаковых расчетах лестниц. Слева все понятно и логично: момент с одним знаком на опорах, с другим – в пролете. Прямо классика. А вот справа лестницу явно штормит. Смена моментов непонятна и нелогична. А если взглянуть на армирование, то вообще за голову схватиться можно – в нижнем марше рабочая арматура окажется сверху, а в самой верхней площадке надопорная арматура будет снизу.

Чем же таким отличаются эти два расчета?

Почему такая разительная разница в результатах? А разница только в одном – в направлении местных осей пластин.

При построение любого трех- или четырехузлового элемента в Лире, ему назначаются местные оси, их можно увидеть, если активировать соответствующий маркер во флагах рисования (“Местные оси пластин”). Направление этих местных осей программа определяет сама и они как-то связаны с очередностью построения элементов. Нам нужно всегда следить, чтобы местные оси пластин совпадали с глобальными – только тогда мы сможем без проблем прочесть результаты расчета. Я для себя поняла, что если я строю 4-узловой элемент вручную или же выполняю построение триангуляцией контура, мне нужно указывать узлы в такой очередности, чтобы контур рисовался против часовой стрелки. Тогда местная ось пластин Z cовпадет с глобальной. Но вот с осями Х и У не все так просто. Их направление тоже зависит от того, где будет первая точка построения контура и в каком направлении вы будете очерчивать контур.

На рисунке выше у меня показаны четыре 4-узловых элемента, которые я строила указанием четырех узлов, с подсвеченными местными осями пластин. Первый элемент я начинала строить из точки 1 и вела построение против часовой стрелки; второй – из точки 2 по часовой; третий – из точки 3 по часовой; четвертый – из точки 4 против часовой. Видите разницу в направлении осей? В нижнем левом углу показаны глобальные оси. Только первый элемент по положению местных осей совпадает с глобальными. У остальных те или иные оси смотрят в разные стороны.

А теперь давайте глянем на плиту, построенную с помощью триангуляции контура:

Эту плиту я строила, начиная из узла 1, обводя против часовой стрелки. В итоге местные оси Z для всех элементов совпадают с глобальными. Это хорошо. Но если взглянуть на оси Х и У – кто в лес, кто по дрова. Программа разворачивает их совсем не так, как нам хочется.

На что может повлиять несовпадение местных осей с глобальными?

Результаты расчета (усилия – моменты, поперечная сила и т.д., армирование) показывается для местных осей, а не для глобальных. Если местные оси сонаправлены с глобальными, мы видим понятную картину – верх совпадает с верхом, низ с низом, левая сторона – с левой, а правая – с правой.

Если не совпадают местная и глобальная оси Z, мы в эпюрах увидим не те знаки (плюс вместо минуса и минус вместо плюса), а в результатах армирования – неправильное положение арматуры (нижняя вместо верхней и верхняя вместо нижней).

Если местная ось Х (или У) оказалась перпендикулярной глобальным осям Х (или У), в результатах усилий и армирования мы получим не то направление (Му вместо Мх и арматуру вдоль У вместо арматуры вдоль Х).

Давайте я поясню эту путаницу на простом примере.

Есть плита, шарнирно опирающаяся по двум сторонам.

Рассчитаем ее в двух вариантах: слева – когда местные оси пластин совпадают с глобальными; справа – когда местная ось Z направлена в противоположную сторону глобальной, а оси местные Х и У повернуты относительно глобальных на 90 градусов.

Давайте сравним результаты расчета.

Перемещения по оси Z:

Как видите, прогибы плит абсолютно одинаковы, местные оси пластин не влияют на закон тяготения – вниз так вниз.

Изгибающие моменты Мх:

А вот тут пошло интересное. Слева картина классическая – плита не работает в направлении глобальной оси Х и момент в ней одинаково близок к нулю. А вот справа нам показаны усилия классического изгибающего момента в плите, только с другим знаком. В центре – момент максимален, на опорах равен нулю. На картинке я постаралась изобразить эпюру изгибающего момента в привычном формате, и вышло, что она в принципе такая, как в классической схеме с шарнирным опиранием по двум сторонам, но только повернута “пузиком” вверх. Почему так вышло? Да просто эпюры усилий в элементах даются с учетом местных осей, а не глобальных. Напомню, мы рассматриваем момент Мх. Местная ось Х в плите слева направлена так же, как глобальная и эпюра выглядит абсолютно предсказуемо. А вот местная ось Х в плите справа направлена вдоль глобальной оси У (непривычный взгляд). И момент Мх в плите показывает ее работу вдоль плиты, то есть вдоль глобальной оси У. Почему же максимальный момент Мх в плите справа отрицательный, а не положительный? Ведь мы привыкли уже, что растяжение в нижней зоне плиты соответствует положительному моменту. Все дело в направлении местной оси Z: так как она направлена сверху вниз – навстречу глобальной оси, момент тоже изменил знак относительно привычного значения.

Видите, как местные оси влияют на результаты расчета! Этот фактор всегда нужно учитывать.

Если вы посмотрите другие эпюры, в них будет та же “путаница”. Но я хочу сразу перейти к армированию.

Изначально нас интересует армирование вдоль оси У, так как именно в этом направлении работает плита. Даже не глядя на арматуру, можно предположить, что нижняя арматура вдоль У будет максимальной в пролете и снижаться к опорам, а верхняя арматура вдоль У будет минимальна, т.к. плита опирается шарнирно. Это предположение полностью оправдывают рисунки левой плиты (см. рисунок выше). Но вот правая плита выдает парадоксальный результат: нижняя арматура в плите как бы вообще не нужна, зато отчего-то нужна верхняя. Будем так армировать? Неа. Мы ведь уже знаем, что в результаты вмешались местные оси пластин – армирование же показывается тоже относительно местных осей элементов. И чтобы разобраться с арматурой, нужно всегда обращать внимание на направление всех осей: местные оси Х и У показывают направление арматуры, а местная ось Z показывает, где в пластине нижняя арматура (ближе к местному нулю по оси Z), а где – верхняя.

На этом я обзор завершаю, дальше вы можете поиграть с результатами расчетов самостоятельно. Единственное, к чему призываю: следите, чтобы по возможности (по крайней мере в горизонтальных элементах) местные оси изначально совпадали с глобальными. А если не совпали, то хотя бы откорректируйте их, Лира дает такую возможность.

И напоследок предлагаю вам просмотреть видео на эту тему, в нем рассматривается ситуация, когда при расчете лестницы местные оси пластин были направлены по воле случая.

Источник