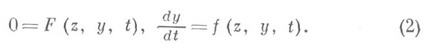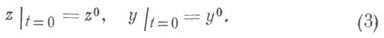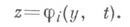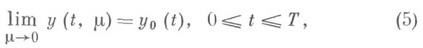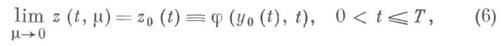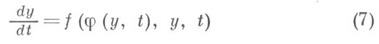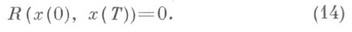Метод малого параметра дифференциальные уравнения
Метод малого параметра
Нелинейные дифференциальные уравнения иногда решают путем последовательных приближений, представляя искомую величину х в виде ряда по степеням некоторого коэффициента ц, который называют малым параметром:
где х0 — решение уравнения нулевого приближения (последнее получают из исходного, полагая, что все нелинейные члены в исходном уравнении отсутствуют); х1 — решение уравнения первой поправки, которая учитывает влияние нелинейных членов в первом приближении; х2 — решение уравнения второй поправки и т. д.
Если исходное уравнение является дифференциальным уравнением второго или более высокого порядка, а принужденный режим представляет собой колебательный процесс, то квадрат угловой частоты первой гармоники о 2 или первую степень со также разлагают в ряд по малому параметру:
где cOq — квадрат угловой частоты в нулевом приближении, когда всеми нелинейными членами пренебрегают; х/г — поправка первого приближения, вызванная нелинейными членами уравнения; ц 2 /2 — поправка второго приближения и т. д.
Последовательность решения рассмотрим на двух примерах.
1. При х(0) = 0 решить уравнение
К такому уравнению, например, сводится задача о переходном процессе в цепи, состоящей из нелинейной индуктивности с нелинейной ВАХ и линейного резистивного сопротивления, при подключении ее к источнику постоянного напряжения и при квадратичной аппроксимации зависимости пото- косцепления от тока.
Линейные члены уравнения переносим в левую часть, а нелинейные, умножив на некоторый малый параметр ц, — в правую (в примере ц = 1):
Представим решение (16.35) в виде ряда по степеням р:
Подставим (16.37) в (16.36):
Из (16.38) образуем систему уравнений, приравняв члены левой и правой частей его при одинаковых степенях ц: уравнение нулевого приближения
уравнение для первой поправки
уравнение для второй поправки.
Постоянную С0 = 0 определили из начальных условий.
Подставим х0 = t в уравнение (16.40) и проинтегрируем его:
Для первой поправки начальные условия также нулевые, поэтому Сх = 0; t 3
=——. Подставим значения х0 и X] в (16.41):
В соответствии с (16.37)
Аналогично можно было бы получить и последующие члены ряда (16.37). Так как уравнение (16.35) имеет точное решение х = tht, то, взяв в разложении tht три первых члена ряда, можно убедиться, что они совпадают с правой частью (16.42).
2. Решить уравнение для лампового генератора (вывод уравнения см. в примере 164) при начальных условиях х(0) = А0, х'(0) = 0:
Коэффициент кг при нелинейном члене в дальнейшем будем считать малым параметром и обозначим р. В соответствии с предыдущим
Образуем из (16.45) три уравнения, соответствующих р в нулевой, первой и второй степенях:
Проинтегрируем (16.46): х0 =A0cos wt.
Подставив х0 в (16.47) и учтя, что sinacos 2 a = 0,25sina + 0,25sin3a, получим 
Уравнение (16.49) можно трактовать следующим образом: на колебательный LC-контур без потерь (левая часть уравнения (16.49)) воздействуют вынуждающая сила с угловой частотой со, равной собственной частоте колебательного контура, и сила с угловой частотой, в три раза большей.
Известно, что если подключить колебательный LC-контур, имеющий активное сопротивление R —> 0, к источнику синусоидальной ЭДС Emsin cot при оговоренных условиях, то амплитуда тока в цепи будет нарастать до бесконечности. Действительно,
При R —> 0 v-> 0 и 5 = R/(2L)-> 0.
В результате получим i
Такие члены в решении дифференциальных уравнений, амплитуды которых нарастают теоретически до бесконечности при увеличении времени t, называют вековыми. При дальнейшем решении уравнения (16.49) необходимо помнить о том, что амплитуды вековых членов должны оказаться равными нулю при любом t > 0.
Решение (16.49) запишем следующим образом:
Первое и второе слагаемые представляют собой полное решение однородного уравнения; четвертое и пятое — частное решение неоднородного уравнения. Третье слагаемое представляет собой вековой член. Его можно было бы не вводить в дальнейшие выкладки по определению коэффициентов Аь В1з Еь FX,CV Db однако введем его, чтобы показать, что его присутствие выкладкам не помешает.
Дважды продифференцируем (16.50) по времени:
Подставим (16.50) и (16.51) в (16.49), выделим из левой и правой частей (16.49) слагаемые соответственно с sin cot (формула (16.52)), coscot (формула (16.53)), sin3cot (формула (16.54)), cos3cot (формула (16.55)):
Слагаемые (16.49) с вековыми членами дают нуль:
Используем также заданные начальные условия для определения Аь Вг, Сь Db Еь Fv Так как начальные условия уже были удовлетворены при определении л:0, то для всех последующих приближений начальные условия нулевые. Имея это в виду, из (16.50) находим ^(0) -B1 + F1 = 0.
В соответствии с (16.55) Fx = 0, поэтому Вг = 0. Из уравнения (16.50), используя условие х <= 0, получим
Но Ег известно из (16.54), поэтому
Поправку на угловую частоту/^ а вместе с тем и значение А0 найдем исходя из того, что амплитуда векового члена должна быть равна нулю при любом f > 0. Отсюда Сг = 0 и Dx = 0.
Из (16.53) следует, что/г = 0, а из (16.52) — что А0 = 2.
Ограничившись первым приближением и перейдя от р к кг, получим
Первое прибл ижение привело к изменению амплитуды первой гармоники
с Л0 = 2 до Дэ = 2 J1 +1 —-—- I и к появлению третьей гармоники.
Угловая частота первой гармоники в первом приближении не изменилась и равна угловой частоте ш0 нулевого приближения. Аналогично производится и второе приближение. Однако каждое последующее приближение по сравнению с предыдущим более трудоемко.
В основу данного метода положены работы французского математика Пуанкаре по небесной механике. Метод называют методом малого параметра, потому что в нем выполняют разложение решения в ряд по степеням малого параметра. Насколько этот параметр должен быть мал в каждом примере, заранее сказать нельзя. Важно, чтобы ряды для х и для о) 2 или со сходились. Если ряды будут сходиться медленно или вообще не будут сходиться, то пользоваться этим методом не имеет смысла.
Метод малого параметра
Метод малого параметра
Боголюбова, Ю. А. Митропольский. Напишите желаемое периодическое решение в следующем формате х-ХL iLXl ntxi … 2 часа дня. Где x0, xi x-неизвестная периодическая функция частот, кратных циклическим частотам p и p, определяемая later. At одновременно разверните p — 2 нужной круговой частоты-с мощностью малого параметра p. п а АИП ПДП… 3 часа дня. Где ocj, a4-постоянный коэффициент, который определяется при интегрировании Формулы 1.
При вычислении момента инерции однородной плоской фигуры относительно некоторой оси выделяют в плоской фигуре такую элементарную площадь, момент инерции которой относительно соответствующей оси известен, либо легко может быть подсчитан. Людмила Фирмаль
Значения Oj, a выбираются таким образом, чтобы решение 2 было периодическим, то есть не содержало так называемых резонансных или долговременных членов, которые растут бесконечно с time. To для ясности предположим, что при решении задачи необходимо интегрировать дифференциальные уравнения. У1 п х м грех ст НТ грех 3 ПТ… Коэффициент Mt зависит от at. Среди конкретных решений этого уравнения есть бесконечно возрастающее резонансное решение-cos pt. To чтобы искомый закон движения был цикличным, необходимо учесть M равное нулю. Искомый коэффициент a определяется по формуле Mi 0. Решите задачу указанным методом и определите следующий закон свободных нелинейных колебаний.
Рекомендуется в следующем порядке 1 Создайте дифференциальное уравнение движения 1, представленное в виде—p f x 0. 2 используя формулы 2 и 3, в разложении мощности малого параметра p опишем искомый закон движения x и неизвестную мощность 2 круговой частоты p. 3 вычислить I и I, используя формулу 2 4 заменить значения x, I и I в абзаце. 2 и 3 подраздел 1 дифференциал equations. At в то же время замените коэффициент а с помощью Формулы 3.То есть, ki-pt-a1p, — a ii— …И еще write. As результатом этих подстановок является дифференциальное уравнение с членами, содержащими малый параметр p различной степени obtained. In кроме того, без членов p А. А. Андронов, А. А. Вит, О. Е.
Используя начальные условия 7, интегрируем дифференциальное уравнение X0 p9×0 0 и x0 0 9 ввести полученную формулу xe t в дифференциальное уравнение я Р Х Fi в ОИ. х0 После простой тригонометрии с правой стороны мы получаем следующую форму п Х2 l1x потому что ПТ потому что 3 ф… Чтобы не увеличиваться бесконтрольно со временем, его следует считать равным нулю. Определите C из уравнения 0. 10 используя начальные условия движения в пункте 7 интегрировать дифференциальное уравнение А Х1 Н COS на 3 ПТ… определите xj f.
Значения x0 0, ots и x1 0-это пункт 8, 9 и 10 вставить в дифференциальное уравнение А Р2 1 ф я а ХV ХД. Повторите расчет, а также расчет абзаца. 9 и 10, А и Х2 0 и т. д 12 определите искомые значения x 0 и p9, пункт 2 и введите расчетные значения xv 0, aj Xj 0, a2, x2 0 и т. д При решении задачи строки 2 и 3 обычно усекаются терминами, включающими p или A. ниже приведен пример х х0 jxx1 p2×2, Р2 А2 СА1 п a9. Задача 20.2.Используя метод малых параметров, определите уравнение физического маятника конечной амплитуды и частоту круговых колебаний, если P — его вес. I-расстояние от оси подвески z до центра тяжести см. рисунок, а 1-момент инерции маятника относительно подвески axis.
До члена, содержащего малый параметр p первого порядка, уравнение принимает вид Fo 4-R Fo I F1 F1 1fo-FY 0. а также коэффициенты в скобках без p, если мы уравняем члены уравнения без p до нуля ФО Фо О, 8 Ф1 ргУ1 1фо Ф5 — 9 Учитывая начальные условия t 0, p aQ, 0, используя уравнение 0 Фо 0 нф1 0 О О Ф О нФ О пиши ФО 0 ЛF1. О Фо о ЛF1 о. В каждом из этих уравнений члены без p и с p слева и справа делаются равными начальным условиям функций 0 0 и 1. ФО 0 АО. Ф1 О. ФО О. Ф1 0 0.
Если в ходе решения задачи требуется вычислить момент инерции твердого тела относительно оси, не проходящей через центр тяжести, то проводят параллельную ось через центр тяжести твердого тела и применяют теорему Штейнера (при этом момент инерции твердого тела относительно оси, проходящей через центр тяжести, масса твердого тела и расстояние между параллельными осями должны быть известны). Людмила Фирмаль
Где формула 12 имеет вид i p4i 4a8cos3P О4 Его общее решение fx равно сумме F1 f, 11 f, 1, 15 Где f — частное решение уравнения 14, а f 1 — общее решение соответствующего однородного уравнения F1 p ph1-0.In это дело Ф Ф 1 Ди cospt да грех, пт, ТП Альф соз 3 ПТ Ф И f — Если вы назначите 9apcos 3pt формуле 14, вы найдете a — atsthr1.Теперь общее решение 15 можно записать следующим образом Форекс ДХ, потому что ПТ да грех пт-потому что 3 ПТ 16 Функция 16 и ее производная по времени —DJ slnjrf d2pcos RF — sin3pf Начальные условия движения 10 7 0, 0 0, 1 0 0, поиск.
Как видно из Формулы 20, маятник колеблется по закону 20 на частоте кривизны Р 18, которая зависит от начального отклонения маятника А0.Поэтому вибрации нет isochronous. In другие слова Условия эксплуатации. Напомним, что приближенное линейное дифференциальное уравнение A p 0 соответствовало изохронным гармоническим колебаниям 3 p a0cos6f. поэтому даже приближенное решение нелинейных уравнений, выполненных в этой задаче, смогло обнаружить отсутствие изохронности колебаний. Влияние начального углового отклонения маятника a0 на круговую частоту p равно small.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Дифференциальные уравнения с малым параметром при производной
Возьмем дифференциальное уравнение (где — параметр)
Если функция в некоторой замкнутой области изменения непрерывна по совокупности аргументов и удовлетворяет условию Липшица по
Во многих задачах физики приходится рассматривать уравнения вида (где — малый параметр)
Вопрос ставится так: при каких условиях для малых значений в уравнении (2) можно отбросить член и в качестве приближения к решению дифференциального уравнения (2) рассматривать решение так называемого «вырожденного уравнения»
Достаточные условия устойчивости или неустойчивости выражаются следующими предложениями.
1. Если на решении уравнения (4), то решение вырожденного уравнения устойчиво.
2. Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG0AAAAuBAMAAADQGoqnAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAnpQBwUdnMSEQgeDwsdDVhGY9AAAC90lEQVRIx61UTUhUURT+nDs/b6yRcVNCQdIPES66MOgirRnyJ8zISW0RJDObQJzFzNCsgnCMatNiJoso0pqFpERhqAVuGkgTFMyCWoUpSUEbw0atrKRz541vRl5XfdBdvHvfOee755zvnHuA/7Ps0bX/0fWMyx7ExaZ4gZuhtarW9Xwcb3gp9u6PQPVaFTvsl+PMfn6W4rEtLcBaCVgTOTrlhxwXm4G7GDCletBJoW715CoL5biOEArItmAWCDCgLdcffHE58EKvOwW4ncAUpRQ8n8mNM05SrxTW9bnZV4nI18FiNg68TVap5Hf3XySiCoqldM5x++Rr8tMItgi4Jlxpcb7//tg0h9kjw5nIuJ7oPhiHZVHQqoovI7ZngrSVUjoHwCYptDqkcWXfVfFtBEVq+SkZLuiEskA0/FFxDs1wF18Px/r8KBPxLVOqtFd4bKqcDYJOjlmpPy/uOlVfbEmUrwth6lJfyzfRnVJeWGfCPkf7oZ90Pkq4M8fQ9wTsUfiFrRYoT8j82Z6fEDqzCKibwzQSQmSY+KyJTBFbMXndFdEgrEIUOEZdRWwwQT4XJwS4zr60MednZ5t4eXlqVIpTy+KZDmbtL8k+UvbqcRowpL4sTVE6o8P5vNax7F/TgfTWnP5e0cTXMjdYejXRe7DlrD81DWZN0+DS5D3avUWrliNgK/qkXbJyNW3PsLgAVs8NjLpmdfZYjOLQXs1VHAjHGnZvtLTL25/m+DtVuNHScJc+ifYiXJKvErmpOGuELSPcLyPphau1+s0bgDW9W+2XkFU/jFt7ZLAirT9HA7rhf29f4N9zz1KU7YyrLTr1XiijG0asbyk2ycVYM77OZaaY0WV76K+PshvS7patktOtSR6pC38IGYLlDcH8W6k1LfkShnBBP/Ln80KOVMCQP5aMwkHjt9xjkJUVwgzQNDQWJSzUrz6/PR702uJGcArNqZN8y/A0P2KsiDvi17/AvT95Z5uxQDtGxuOwvrlV5TVYdxfH5nrlL0fPxey1y4iJAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> на решении уравнения (4), то решение вырожденного уравнения неустойчиво.
В полуустойчивом случае, как правило, нельзя заменять решение исходного уравнения (2) решением вырожденного уравнения (4).
Можно указать критерии, когда интегральные кривые уравнения (2) при соответствующем выборе начальной точки приближаются к решению вырожденного уравнения и остаются в его окрестности при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, однако это справедливо лишь при отсутствии возмущений уравнения (2).
Приведем эти критерии.
Пример 1. Выяснить, стремится ли решение уравнения
Пример 2. Исследовать на устойчивость решение вырожденного уравнения для уравнения
так что решение устойчивое
так что решение вырожденного уравнения неустойчивое (рис. 51).
Пример 3. Исследовать на устойчивость решение вырожденного уравнения, отвечающего уравнению
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ
В наиболее законченной форме результат был дан А. Н. Тихоновым [1]. В общих чертах он состоит в следующем. Пусть уравнение F(z, у, t)=0 определяет в нек-рой замкнутой ограниченной области Dнесколько изолированных корней
Введем так называемую присоединенную систему
где yo(t)находится из системы
при начальном условии y0|t=0=y 0 ; T связано с размерами области D. Таким образом, в отличие от регулярного случая близость при малых m решения x(t,m)системы (1) к решению системы, в к-рой положено m=0, т. е. системы (2), имеет место только при специальных условиях.
Предельный переход (6) не является равномерным в связи с тем, что, вообще говоря,
Иными словами, в связи с «потерей» начальных условий для z, и в окрестности t=0 имеется (правда, бесконечно сужающаяся при 
) область, где z(t,m). и z0(t)не близки. Это явление получило название явления пограничного слоя (название заимствовано из гидродинамики).
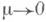
Понятие устойчивости корня z=j(y, t )играет большую роль при исследовании системы (1). Различным критериям устойчивости точки покоя по Ляпунову (см. Устойчивость по Ляпунову )соответствуют различные критерии устойчивости корня z=j(y, t). Наиболее употребителен критерий первого приближения, состоящий в требовании, чтобы собственные значения Xматрицы
удовлетворяли неравенству Re l 0, то для задачи (1), (3) имеет место результат, аналогичный описанному выше, но для t 0. (Подробное описание алгоритма построения асимптотич. разложения решения задачи (1), (3) дано в [2]; там же доказано, что остаточный член асимптотич. разложения (13) при достаточной гладкости правых частей (1) имеет порядок O(m n+1 ) равномерно относительно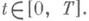 
) Подобного же рода асимптотич. разложение имеет место для решения задачи (1), (10), (11). Отличие заключается в том, что в этом случае к степенному разложению типа (12) добавляются уже два пограничных ряда в связи с наличием пограничного слоя в окрестности и t=0, и t=T.
Асимптотич. представление (13) (при наличии устойчивого корня) или аналогичное ему представление с двумя пограничными слоями (при наличии условно устойчивого корня) дает возможность доказать существование и получить асимптотику решения задач с более сложными дополнительными условиями, чем (3) или (10), (11) (см. [2]):
Существует много работ, посвященных отдельным весьма разнообразным задачам, напр., таким, как исследование случаев обращения Re Xв нуль, исследование (1) на бесконечном промежутке, изучение решения начальной задачи с сингулярными по m начальными значениями z, изучение (1) в абстрактной форме и др. (см. обзор [4]). Большое количество исследований посвящено линейным уравнениям типа (1). Для линейных уравнений одной из характерных задач является задача исследования асимптотики собственных значений и собственных функций (см., напр., [5]), построение асимптотики фундаментальной системы решений в целом. Исследование последнего вопроса сильно затрудняется, если в системе имеются так наз. точки поворота (подробный обзор этого рода проблем см. в [4]).
Ряд результатов, полученных для дифференциальных уравнений типа (1), был перенесен на интегро-дифференциальные уравнения с малым параметром при производных (см., напр., [6]). Имеется также значительный круг работ, посвященных уравнениям с частными производными, содержащими при старшей производной малый параметр (см., напр., [5], [7]). Совершенно аналогичные асимптотич. закономерности наблюдаются для дифференциально-разностных уравнений в случае малого отклонения аргумента (см. [4]).
Смотреть что такое «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ» в других словарях:
МАЛОГО ПАРАМЕТРА МЕТОД — в т е о р и и дифференциальных уравнений приемы построения приближенных решений дифференциальных уравнений и систем, зависящих от параметра. 1) М. п. м. для обыкновенных дифференциальных уравнении. Обыкновенные дифференциальные уравнения, к к рым … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ — уравнение, в к ром неизвестной является функция от одного независимого переменного, причем в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков. Термин дифференциальные уравнения был предложен Г.… … Математическая энциклопедия
Быстро-медленная система — Фазовый портрет быстро медленной системы; зеленым показана устойчивая часть медленной поверхности, красным неустойчивая … Википедия
КОЛЕБАНИИ ТЕОРИЯ — раздел прикладной теории дифференциальных уравнений, связанный с изучением колебательных явлений в естествознании и технике. Основные проблемы К. т. состоят в доказательстве существования и фактич. отыскании колебательных (периодических, почти… … Математическая энциклопедия
РЕЛАКСАЦИОННОЕ КОЛЕБАНИЕ — периодический процесс, при к ром медленное, плавное изменение состояния объекта в течение конечного промежутка времени чередуется с быстрым, скачкообразным изменением его состояния за бесконечно малое время. Такие колебательные процессы… … Математическая энциклопедия
НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ — колебания в физич. системах, описываемые нелинейными системами обыкновенных дифференциальных уравнений где содержит члены не ниже 2 й степени по компонентам вектора вектор функция времени малый параметр (либо и ). Возможные обобщения связаны с… … Математическая энциклопедия
Олейник, Ольга Арсеньевна — (род. 2.7.1925) советский математик. Род. в Матусове (Киевская обл.). Окончила МГУ (1947). Д р физико матем. наук (1954), проф. (1955). С 1955 работает в МГУ. Науч. интересы О. сформировались под влиянием И. Г. Петровского. Осн. труды по… … Большая биографическая энциклопедия
ВОЗМУЩЕНИЙ ТЕОРИЯ — комплекс методов исследования различных задач, используемый во многих разделах математики, механики, физики и техники. Здесь с общей точки зрения излагаются основные идеи В. т. В. т. основана на возможности приближенного описания исследуемой… … Математическая энциклопедия
ПОГРАНИЧНОГО СЛОЯ ТЕОРИЯ — асимптотическое приближение решения граничных задач для дифференциальных уравнений с малым параметром при старших производных (сингулярных задач) в подобластях с существенным влиянием членов со старшими производными на решение. Явление… … Математическая энциклопедия
Иманалиев, Мурзабек Иманалиевич — В Википедии есть статьи о других людях с такой фамилией, см. Иманалиев. Мурзабек Иманалиевич Иманалиев Дата рождения: 13 сентября 1931(1931 09 13) (81 год) Место рождения: Каинды, Киргизская АССР, РСФСР, СССР (ныне … Википедия