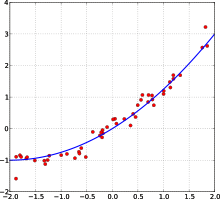
Метод наименьших квадратов метод нахождения оценок параметров регрессии основанный на минимизации

Математика на пальцах: методы наименьших квадратов

Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.

Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.

Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.

Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.

Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.

Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.

Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:

Эта прямая должна иметь уравнение типа следующего:

Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:

Можно записать это уравнение в матричном виде:

Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.

Давайте заменим конкретные матрицы на их символьное представление:

Тогда (alpha, beta) может быть легко найдено:

Более конкретно для наших предыдущих данных:

Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):

Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):

Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:

И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:

В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha\*i + beta\*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:

И будем стараться минимизировать эту ошибку:

Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.

Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:

UPDATE: тут у меня косяк, расстояние до прямой должно измеряться по вертикали, а не ортогональной проекцией. Вот этот комментатор прав.

Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:

Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.

Минимум квадратичной формы

Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:

Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:

Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:

Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:

Вся эта гимнастика известна под именем линейной регрессии.

Уравнение Лапласа с граничным условием Дирихле

Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:

Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:

X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.

Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.

Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:

В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:

Давайте вдвое усилим пружинки между вершинами:

Логично, что поверхность стала более гладкой:

А теперь ещё в сто раз сильнее:

Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.

Уравнение Пуассона

Давайте ещё крутое имя вспомним.

Предположим, что у меня есть такая картинка:

Всем хороша, только стул мне не нравится.

Разрежу картинку пополам:

И выделю руками стул:

Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:

Код и картинки доступны здесь.

Пример из жизни

Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:

У меня есть некоторое количество фотографий образцов ткани типа вот такой:

Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:

Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:

Вот фрагмент, где чётко видно шов:

Поэтому я вырезать буду не по ровной линии, вот линия разреза:

А вот повторённый четыре раза паттерн:

И его фрагмент, чтобы было виднее:

Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:

Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.

Источник

Метод наименьших квадратов

Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.

Содержание

Сущность МНК

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

где — вектор неизвестных параметров модели

— случайная ошибка модели.

Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть — номер наблюдения (). Тогда — значения переменных в -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:

Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков (англ. Residual Sum of Squares [1] ) будет минимальной:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares ). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:

Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).

МНК в случае линейной модели

Пусть регрессионная зависимость является линейной:

Пусть y — вектор-столбец наблюдений объясняемой переменной, а — матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):

.

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

Для аналитических целей оказывается полезным последнее представление этой формулы. Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.

Пример: простейшая (парная) регрессия

В случае парной линейной регрессии формулы расчета упрощаются (можно обойтись без матричной алгебры):

Свойства МНК-оценок

В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если

Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок

Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.

Обобщенный МНК

Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков , где — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение . Следовательно, указанный функционал можно представить следующим образом , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

Ковариационная матрица этих оценок соответственно будет равна

Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

Взвешенный МНК

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.

Некоторые частные случаи применения МНК на практике

Аппроксимация линейной зависимости

Рассмотрим случай, когда в результате изучения зависимости некоторой скалярной величины от некоторой скалярной величины (Это может быть, например, зависимость напряжения от силы тока : , где — постоянная величина, сопротивление проводника) было проведено измерений этих величин, в результате которых были получены значения и соответствующие им значения . Данные измерений должны быть записаны в таблице.

Таблица. Результаты измерений.

№ измерения
1
2
3
4
5
6

Вопрос звучит так: какое значение коэффициента можно подобрать, чтобы наилучшим образом описать зависимость ? Согласно МНК это значение должно быть таким, чтобы сумма квадратов отклонений величин от величин

Сумма квадратов отклонений имеет один экстремум — минимум, что позволяет нам использовать эту формулу. Найдём из этой формулы значение коэффициента . Для этого преобразуем её левую часть следующим образом:

Далее идёт ряд математических преобразований:

Последняя формула позволяет нам найти значение коэффициента , что и требовалось в задаче.

История

Альтернативное использование МНК

Идея метода наименьших квадратов может быть использована также в других случаях, не связанных напрямую с регрессионным анализом. Дело в том, что сумма квадратов является одной из наиболее распространенных мер близости для векторов (евклидова метрика в конечномерных пространствах).

Одно из применений — «решение» систем линейных уравнений, в которых число уравнений больше числа переменных

,

где матрица не квадратная, а прямоугольная размера n» border=»0″ />.

Такая система уравнений, в общем случае не имеет решения (если ранг на самом деле больше числа переменных). Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений

Используя оператор псевдоинверсии, решение можно переписать так:

,

где — псевдообратная матрица для .

Данную задачу также можно «решить» используя взвешенный МНК, когда разные уравнения системы получают разный вес из теоретических соображений.

Естественно, данный подход может быть использован и в случае нелинейных систем уравнений.

Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.

См. также

Примечания

Литература

Ссылки

Смотреть что такое «Метод наименьших квадратов» в других словарях:

Метод наименьших квадратов — метод статистической оценки функциональной зависимости путем установления таких ее параметров, при которых сумма квадратов отклонений опытных данных от этой зависимости является минимальной. Источник: ГОСТ 20522 96: Грунты. Методы статистической… … Словарь-справочник терминов нормативно-технической документации

метод наименьших квадратов — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] метод наименьших квадратов Математический (математико статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными … Справочник технического переводчика

Метод наименьших квадратов — [least square technique] математический (математико статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление … Экономико-математический словарь

Метод Наименьших Квадратов — статистический метод определения параметров генеральной совокупности путем минимизации критериев суммы квадратов отклонений между фактическими и расчетными данными. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

Метод наименьших квадратов — метод определения коэффициентов полиномиальной аппроксимирующей функции, основанный на минимизации суммы квадратов отклонений значений аппроксимирующей функции от исходных данных. Источник: АНАЛИЗ ПОВОЗРАСТНЫХ РИСКОВ СМЕРТНОСТИ НАСЕЛЕНИЯ.… … Официальная терминология

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ — метод оценки параметров по наблюденным данных причем оценки должны быть несмещенными (см. Оценка несмещенная) и Е(Т θ)2 минимально, где в параметр, Т его оценка, Е математическое ожидание. В качестве Т берут определенную функцию от… … Геологическая энциклопедия

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ — англ. method, least squares; нем. Methode der kleinsten Quadrate. Применяются, напр., для исчисления коэффициентов регрессии. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии

метод наименьших квадратов — minimaliųjų kvadratų metodas statusas T sritis automatika atitikmenys: angl. least squares method; method of least squares vok. Methode der kleinsten Quadrate, f rus. метод наименьших квадратов, m pranc. méthode de plus petits carrés, f; méthode… … Automatikos terminų žodynas

метод наименьших квадратов — mažiausiųjų kvadratų metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Metodas, kuriuo randami skirstinio nežinomųjų parametrų statistiniai įverčiai. atitikmenys: angl. least squares method; method of least squares vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

метод наименьших квадратов — mažiausiųjų kvadratų metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Metodas, naudojamas lygties koeficientams apskaičiuoti, kai pasirenkama ypatinga lygties forma tam, kad būtų galima pritaikyti kreivę prie duomenų.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник