Метод наименьших квадратов мнк может применяться для оценки параметров исходной регрессионной
Метод наименьших квадратов
Метод наименьших квадратов (МНК) — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Данный метод применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
При применении МНК используется подстановка в начальные уравнения неизвестных величин. При этом в правых частях уравнений получаются если не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.
Двухшаговый МНК. Системы одновременных уравнений
ДМНК состоит в следующем:
составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют ДМНК, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели;
обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
Взвешенный МНК
Взвешивание применяется для оценивания коэффициентов модели Y = X β + ε в предположении гетероскедастичности остатков 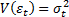
Случай сводится к стандартной модели множественной линейной регрессии с гомоскедастичными остатками несложным преобразованием:
Оценивание полученной модели выполняется стандартным МНК.
Доступный обобщенный МНК
В случае линейной регрессионной модели Y = X β + ε в предположении распределения остатков ε по закону N (0, σ 2 Ω) с заданной матрицей ковариаций Ω, оценка доступного обобщенного метода наименьших квадратов реализуется формулой:
При наличии в модели константы, подлежащей автоматическому оцениванию, следует дополнить матрицу X единичным столбцом.
Метод наименьших квадратов мнк может применяться для оценки параметров исходной регрессионной модели в форме
2.2. Оценка параметров линейной модели по методу наименьших квадратов (МНК)
Этот метод и многочисленные его модификации являются основными и в эконометрике. Поэтому при изучении данного курса ему нужно уделить особое внимание.
2.2.1. Критерий наименьших квадратов. Сравнение с другими возможными критериями
Запишем уравнение для отдельных наблюдений (реализаций) в парной линейной регрессии
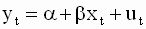 |
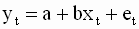 |
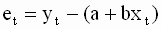 |
Уравнение ( 2.6 ) выражает эмпирическую взаимосвязь между переменными модели и его можно записать только относительно конкретных наблюдений. Подчеркнем, что ошибки модели являются наблюдаемыми величинами, поскольку их можно определить исходя из наблюдений переменных модели.
В методе наименьших квадратов оценки a и b параметров модели строятся так, что бы минимизировать сумму квадратов ошибок (остатков) модели по всем наблюдениям. Таким образом, критерий (целевая функция) наименьших квадратов записывается в виде
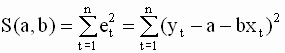 |
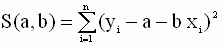 |
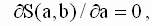 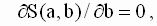 |
которую необходимо решить относительно переменных a и b. По правилам вычисления производных получим следующие выражения:
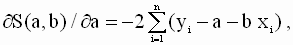 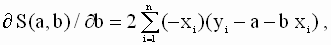 |
так что значения параметров a и b, минимизирующие квадратичную форму ( 2.8 ), удовлетворяют соотношениям
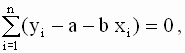 | ||||||||||||||||||||
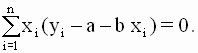 |
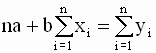 | ||||||||||||||||||
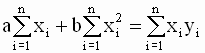 |
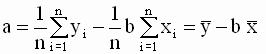 |
где 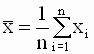
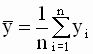
Подставив выражение для a во второе уравнение системы, получим
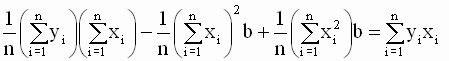 , , |
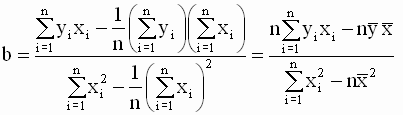 , , |
Таким образом, мы получили следующие соотношения для оценок параметров модели
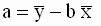 , , |
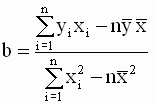 |
Однако, в теоретических исследованиях и практических расчетах чаще используют другую, более удобную эквивалентную форму записи уравнений для оценок. Эта форма получается, если использовать следующие соотношения
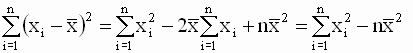 |
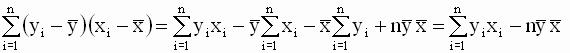 |
Эти соотношения позволяют получить новую форму записи выражения для b (в отклонениях от выборочных средних значений)
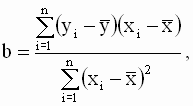 |
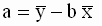 |
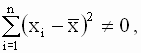 |
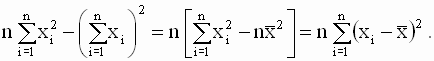 |
Выражение для коэффициента b часто записывают также, используя понятия выборочной вариации (дисперсии) и выборочной ковариации.
Выборочная вариация определяется соотношением вида
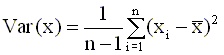 |
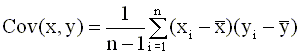 |
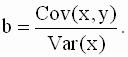 |
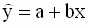 |
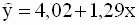 |
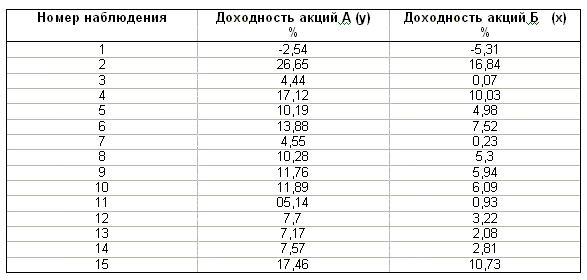
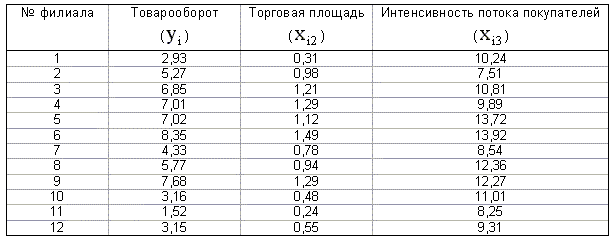
Торговое предприятие имеет несколько филиалов. Исследуем зависимость годового товарооборота отдельного филиала от: а) размера торговой площади; б) среднедневной интенсивности потока покупателей. Поскольку мы пока не умеем строить модели множественной регрессии, построим две «частные» модели парной регрессии.
Таблица 1.2
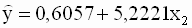 |
Для второй регрессии получаем следующие оценки: a=-2,0394, b=0,6846. Ее уравнение
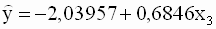 |
Дайте интерпретацию параметров регрессий примера 2.2.
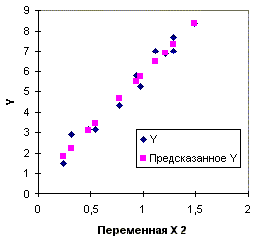
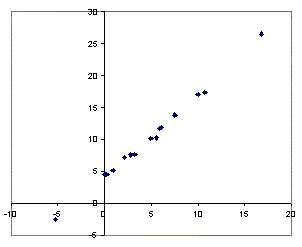
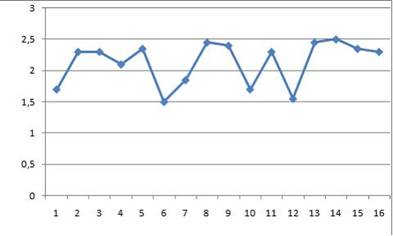
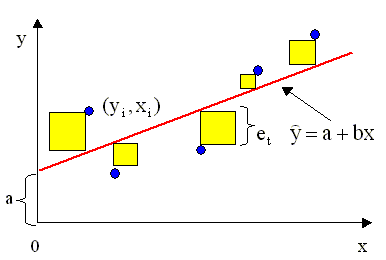
Рис.2.5а. Диаграмма рассеяния и линия
регрессии (первая модель, пример 2.2)
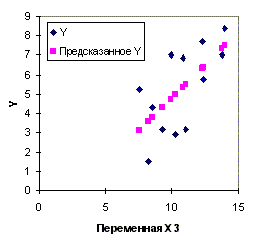
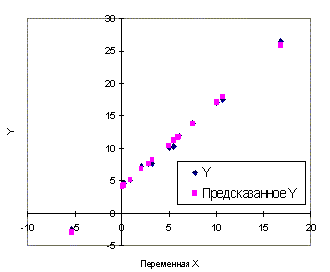
Рис.2.5б. Диаграмма рассеяния и линия
регрессии (вторая модель, пример 2.2)
Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками



+: автокоррелированными и/или гетероскедастичными
-гомоскедастичными и некоррелированными
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
+: линейной
-надежности среднеквадратической ошибки
-ненадежности среднеквадратической ошибки
+: ненадежности оценки
детерминации для модели в исходных показателях равен … Варианты ответов
+: 0,64
При методе наименьших квадратов параметры уравнения парной линейной регрессии 

равенства нулю суммы квадратов
+ минимизации суммы квадратов
125 Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 


+ положительной
126 Исходная регрессионная модель имеет вид 

предпосылки МНК нарушены; традиционного
предпосылки МНК не нарушены; обобщенного
предпосылки МНК не нарушены; традиционного
+ предпосылки МНК нарушены; обобщенного
Если известно уравнение множественной регрессии 
+766,67
Тема208: Обобщенный метод наименьших квадратов (ОМНК)
Пустьy– издержки производства, 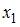
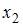
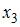
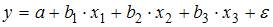
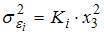
После применения обобщенного метода наименьших квадратов новая модель приняла вид 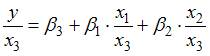
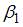





Тема219: Временные ряды данных: характеристики и общие понятия
Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Варианты ответов

Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции 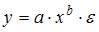
Варианты ответов





Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для стационарных временных рядов y1, у2, … yt, …, yn (t = 1, …, n) автокорреляция зависит только от величины …
Варианты ответов





1)Тема: Предпосылки МНК, методы их проверки
Предпосылками метода наименьших квадратов (МНК) являются следующие …(не менее 2 вариантов ответа)
Варианты ответов
+ 1 отсутствие автокорреляции в остатках
2 присутствие в эконометрической модели более чем двух факторов
3 функциональная связь между зависимой и независимой переменными
+ 4 гомоскедастичность остатков
2)Тема: Оценка параметров линейных уравнений регрессии
Метод наименьших квадратов применим к уравнениям регрессии, …(не менее 2 вариантов ответа)
Варианты ответов
1 которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду
+2 которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду
3 нелинейного вида
+4 которые отражают линейную зависимость между двумя экономическими показателями
3) Тема: Обобщенный метод наименьших квадратов (ОМНК)
Обобщенный метод наименьших квадратов подразумевает … (не менее 2 вариантов ответа)
Варианты ответов
1 переход от множественной регрессии к парной
+2 преобразование переменных
+3 введение в выражение для дисперсии остатков коэффициента пропорциональности
4 двухэтапное применение метода наименьших квадратов
2) Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Несмещенность оценки характеризуется …(не менее 2 вариантов ответа)
Варианты ответов
1 зависимостью от объема выборки значения математического ожидания остатков
+2 равенством нулю математического ожидания остатков
3 максимальной дисперсией остатков
+ 4 отсутствием накопления остатков при большом числе выборочных оцениваний
111.Тема: Структура временного ряда
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
между трендовой, сезонной и случайной компонентами
+первого, второго, третьего и последующих порядков
факторов, формирующих уровень ряда между несколькими временными рядами
118.Тема: Обобщенный метод наименьших квадратов (ОМНК)
При оценке параметров регрессионной модели с гетероскедастичными остатками при помощи обобщенного метода наименьших квадратов (ОМНК) выдвигается предположение, что дисперсия остатков …
+пропорциональна некоторой величине
- Метод наименьших квадратов метод нахождения оценок параметров регрессии основанный на минимизации
- Метод наименьших квадратов сущность и использование для оценки параметров парной линейной регрессии

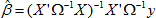
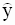 зависимой переменной y уравнением
зависимой переменной y уравнением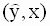 . Эмпирический коэффициент b является частной производной ( 2.19 ) по независимой переменной x (регрессору). Следовательно можно дать следующую интерпретацию коэффициента b: изменение величины независимой переменной x на единицу при фиксированном значении параметра a приведет к изменению оценки переменной y на величину коэффициента b.
. Эмпирический коэффициент b является частной производной ( 2.19 ) по независимой переменной x (регрессору). Следовательно можно дать следующую интерпретацию коэффициента b: изменение величины независимой переменной x на единицу при фиксированном значении параметра a приведет к изменению оценки переменной y на величину коэффициента b.