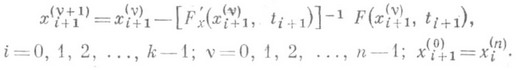Метод продолжения по параметру
Иллюстрированный самоучитель по MathCAD 12
Метод продолжения по параметру
Почему же происходят эти скачки с одного семейства решений на другое? Конечно, причина кроется в выборе начального значения для вычисления каждого из корней. Линия начальных значений х=1 обозначена на графике функции (рис. 5.11) в виде пунктирной вертикальной прямой. Для а0=3, и вообще для нескольких первых а0 начальное значение х=1 находится ближе всего к нижнему семейству решений. Поэтому неудивительно, что численный метод находит именно эти корни. В правой части графика к линии начальных значений ближе второе (верхнее) семейство решений, к ним-то и приводит численный метод.
Приведенные соображения диктуют очень простой рецепт избавления от скачков и нахождения одного из семейств непрерывных решений. Для этого требуется при поиске каждого (i+1)-го корня взять начальное значение, по возможности близкое к отыскиваемому семейству. Неплохим вариантом будет выбор приближения в виде предыдущего 1-го корня, который был найден для прошлого значения параметра а0.
Возможный вариант воплощения этого метода, называемого продолжением по параметру, приведен в листинге 5.18. В нем функция root применена внутри функции пользователя f(x0,a), определенной в самом начале листинга с помощью средств программирования. Назначение функции f (х0,а) заключается в том, что она выдает значение корня для заданного значения параметра а и начального приближения к решению хо. В остальном смысл листинга повторяет предыдущий, за исключением того, что осуществляется поиск сразу обоих семейств решений у и z, причем для каждого сначала явно задается начальное значение только для точки а0. Для всех последующих точек, как следует из последней строки листинга, взято начальное значение, равное предыдущему корню.
Листинг 5.18. Поиск зависимости x(a) решения уравнения ln(ax 2 )=x методом продолжения:

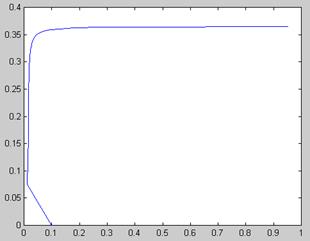
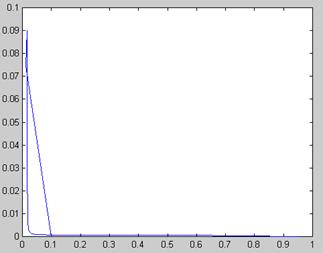
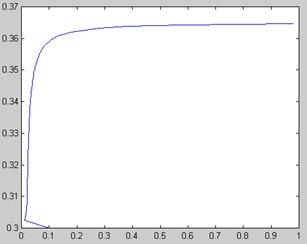
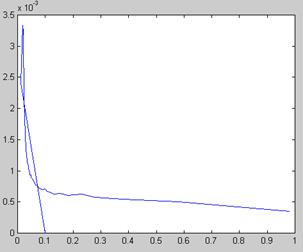
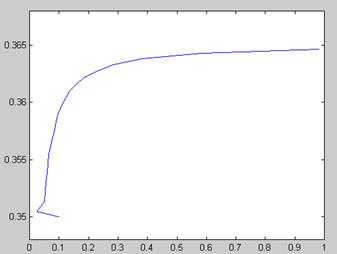
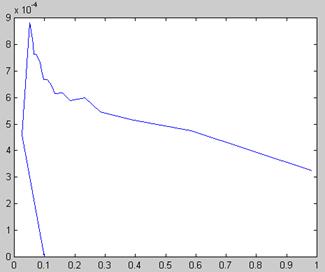
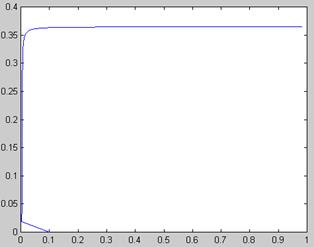
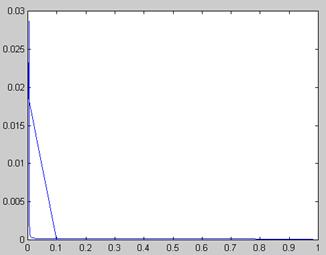
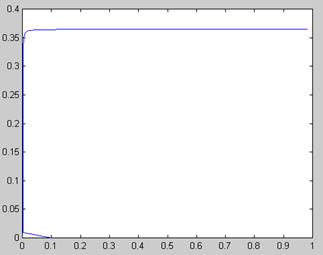
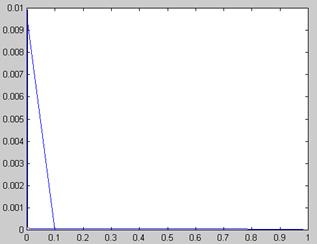
Рис. 5.13. Поиск зависимости х (а) решения уравнения ln(ах 2 ) =х методом продолжения (продолжение листинга 5.18)
Результаты вычислений, приведенные в виде двух графиков на рис. 5.13, разительно отличаются от предыдущего. Как видно, столь малое изменение идеологии применения численного метода привело к определению непрерывного семейства корней. Отметим, что получить результат рис. 5.12 (без продолжения по параметру) в терминах введенной нами в листинге 5.18 функции f(x0,a) можно, изменив ее первый аргумент на константу: f (1,ai).
Примечание
С помощью метода продолжения можно решать и соответствующие задачи оптимизации, зависящие от параметра. Идеология в этом случае остается точно такой же, но вместо функций решения нелинейных уравнений root или Find вам следует применить одну из функций поиска экстремума Minerr, Maximize или Minimize (СМ. разд. 6.1 и 6.2).
Мы привели основную идею и один из возможных способов реализации метода продолжения по параметру. Безусловно, вы можете предложить иные, как математические, так и программистские решения этой проблемы. В частности, для выбора очередного начального приближения к корню можно использовать результат экстраполяции уже найденной зависимости х (а), придумать более сложные алгоритмы для ветвящихся семейств решений и т.д.
Математическая энциклопедия
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД
Пусть, напр., требуется доказать разрешимость в классе Гёльдера задачи Дирихле
в ограниченной N-мерной области 
Вводится семейство эллиптич. операторов
и рассматривается для него задача Дирихле
П. по п. м. (в варианте аналитич. родолжения по параметру) был предложен и развит в ряде работ С. Н. Бернштейна (см. [1], [2]). В дальнейшем этот метод нашел широкое применение в различных вопросах теории линейных и нелинейных дифференциальных уравнений, причем идея аналитич. родолжения по параметру была дополнена более общими функциональными и топологич. принципами (см. [3]).
Лит.:[1] Бернштейн С. Н., “Math. Ann.”, 1904, Bd 59, S. 20-76; [2] его же, Собр. соч., т. 3, М., 1960; [3] Лерэ Ж., Шаудер Ю., “Успехи матеит. наук”, 1946, в. 3/4, с. 71-95. И. А. Шишмарев.
Если разность t i+1 =t i достаточно мала, то значение x i может оказаться достаточно хорошим начальным приближением, обеспечивающим сходимость, для получения решения x i+1 при t=t i+1 (см. [1], [3], [5]).
На практике часто исходная задача естественным образом зависит от нек-рого параметра, к-рый может быть выбран в качестве параметра t.
П. по п. м. иногда наз. также прямой метод вариации параметра (см. [2], [6]), а также комбинированный метод прямого и итерационного методов вариации параметра. В этих методах построение решений обобщенного уравнения сводится путем дифференцирования по параметру к решению дифференциальной задачи с начальными условиями (задачи Коши) методами численного интегрирования обыкновенных дифференциальных уравнений. Применяя простейший метод Эйлера в прямом методе вариации параметра к задаче Коши
Элемент х k будет искомым приближенным решением исходного уравнения Р(х)=0. Уточнение всех или нек-рых значений х i+1 можно проводить итерационным методом вариации параметра [4] (или методом Ньютона). Обобщенное уравнение при этом рассматривается обычно в виде
Метод вариации параметра применен к широкому классу задач как для построения решений, так и для доказательства их существования (см., напр., [3], [4], 16], [7]).
Иллюстрированный самоучитель по MathCAD 12
Метод продолжения по параметру
Решение “хороших” нелинейных уравнений и систем типа тех, которые были рассмотрены в предыдущих разделах этой главы, представляет собой несложную, с вычислительной точки зрения, задачу. В реальных инженерных и научных расчетах очень распространена более сложная проблема: решение не одного уравнения (или системы), а целой серии уравнений, зависящих от некоторого параметра (или нескольких параметров). Для таких задач существуют очень эффективные методы, которые называются методами продолжения. Эти методы непосредственно не встроены в Mathcad, но могут быть легко запрограммированы с помощью уже рассмотренных нами средств. Будем далее говорить об одном уравнении, имея в виду, что всегда возможно обобщение результатов на случай системы уравнений.
Пусть имеется уравнение f (а,х)=0, зависящее не только от неизвестного х, но и от параметра а. Требуется определить зависимость его корня х от параметра а, т. е. х(а). Простой пример такой задачи был приведен в листинге 5.3 (см. разд. 5.1.2). Тогда нам повезло, и решение в общем виде было найдено с помощью символьных вычислений. Рассмотрим еще один, чуть более сложный, пример алгебраического уравнения, зависящего от параметра а следующим образом: ln(ах 2 )=х (рис. 5.11).
Листинг 5.17. Попытка отыскания зависимости x(a) решения уравнения ln(ax 2 )=x:

Рис. 5.11. График функции ln(ах 2 )=х (для а=3 и а=30)
Решим данное уравнение методом секущих, применяя для этого встроенную функцию root. Самый простой, но далеко не лучший, способ иллюстрируется листингом 5.17. Начинается листинг с вывода графика функции ln(ах 2 )=х, корни которой нам предстоит исследовать (ради определенности, для положительных значений х). Глядя на график, сразу можно сказать, что на рассматриваемом интервале уравнение будет иметь два решения (для каждого значения параметра а, больших некоторого порогового значения, ниже которого, видимо, уравнение вовсе не имеет корня).
Для того чтобы получить зависимость решения уравнения от параметра а, в следующих строках листинга создается ранжированная переменная i, с помощью которой определяется вектор значений параметра ai. Его элементы пробегают значения от 3 до 33 с шагом 1(эти числа взяты ради примера, вы можете поэкспериментировать с другими значениями и убедиться в том, что для значений параметра ниже порога а=3 решение уравнения отсутствует).
Последняя строка листинга присваивает элементам еще одного вектора у вычисленные с помощью функции root значения корней уравнения для каждого ai. Но для того чтобы функция root заработала, необходимо предварительно задать начальное приближение к решению, что сделано в предыдущей строке. Ключевой момент метода, примененного в листинге 5.17, заключается в том, что одно и то же начальное значение х=1 использовано для решения уравнения при всех ai.
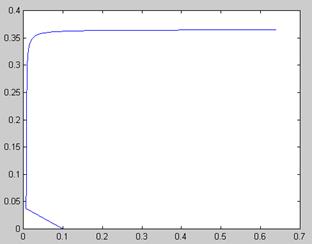
Результат расчетов yi показан на рис. 5.12. Обратите внимание, что по мере увеличения а кривая корней уравнения сначала плавно идет по одному (нижнему) семейству решений, а потом (в районе а=и) явно срывается, “перепрыгивая” на другое семейство. С вычислительной точки зрения такая ситуация чаще всего крайне неблагоприятна, поскольку хотелось бы отыскать непрерывное семейство решений. Скачки зависимости у (а) могут вводить пользователя в заблуждение, вовсе скрывая от него существование нижнего семейства решений при а>n.

Рис. 5.12. Попытка отыскания зависимости х (а) решения уравнения ln(ах 2 )=х (продолжение листинга 5.17)