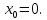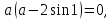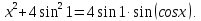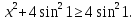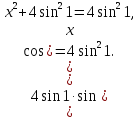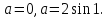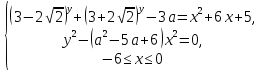Метод симметрии в задачах с параметрами
Симметрия в задачах с параметром
Существует множество задач с параметром, в которых задание ставится следующим образом: «Найдите все значения параметра, при которых уравнение имеет единственное решение». Главным словом здесь будет «единственное». Стоит обратить внимание, что в таких задачах очень часто уравнение не меняется при замене знака одной или нескольких переменных, или при перестановке переменных местами. Этим необходимо пользоваться. Разберем на примерах:
Найдите все значения параметра \(b\), при которых уравнение \(-4x^2+b*cos(sinx )-2b^2\)=0 имеет единственное решение.
Пусть \(
Итак, при \(x=0\) наше уравнение принимает вид \(b-2b^2=0\) ⇔ \(b=0;\) \(b=2;\) Мы нашли значения параметра, при которых у нас возможно единственное решение. Но еще нужно проверить, а будет ли при этих значениях параметра решение единственным. Просто подставим в исходное уравнение.
При \(b=0\) получаем: \(-4x^2=0\) ⇔ \(x=0\) – решение единственное.
Левая часть данного уравнения больше 8, а так как область значения \(cos(x ∈[-1;1])\), то максимальное значение правой части равно 2. Получившееся уравнение не будет иметь корней. При \(b=2\) корней нет.
Найдите все значения параметра \(a\), при которых система
имеет единственное решение.
Заметим интересную особенность:
Наша система симметрична относительно переменной \(y\). А значит, если \((
Решив систему, найдем значения параметра \(a\):
Проверим каждое значение параметра, подставив в условие задачи.
При \(a=-1\) наша исходная система имеет вид:
Попробуем оценить первое уравнение. Напомним, что сумма двух взаимно обратных величин всегда больше равна 2: \((3-2\sqrt<2>)^y+(3+2\sqrt<2>)^y≥2. \)
\(x^2+6x+2≤2\), при \(-6≤x≤0\). (см. рис. 20)
Симметрия в задачах с параметром
Рассмотрены задачи с параметром, имеющие “симметрию” относительно знака или “симметрию” относительно перестановки переменных. Материал полезен при подготовке к ЕГЭ по математике.
Просмотр содержимого документа
«Симметрия в задачах с параметром»
«Симметрия» в задачах с параметром
Определенную группу задач с параметром составляют задачи, в формулировке которых ключевым является слово «единственное». В этих задачах требуется найти все значения параметра, при которых уравнение (неравенство, система) имеет единственное решение. Эти задачи имеют особенность: их условия не изменяются при замене знака одной или нескольких переменных («симметрия» относительно знака) или при перестановке нескольких переменных («симметрия» относительно перестановки переменных). Эта особенность – ключ к решению задачи.
Найти все значения параметра a, при которых уравнение
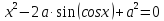
Если число x0 является решением данного уравнения, то и число 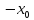
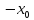
При 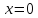
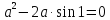
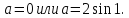
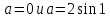
Пусть 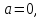
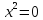
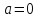
Пусть 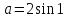
Оценим обе части полученного уравнения. Так как 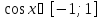
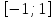
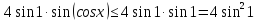
Левая часть
Поэтому уравнение 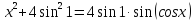
Единственным решением этой системы является х = 0. Значит, 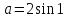
Ответ:
Найти все значения параметра 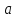
имеет единственное решение.
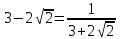
Решая второе уравнение системы, имеем:
или 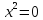
Подставим х = 0 в первое уравнение:
Итак, допустимые значения параметра:
Проверим, какие из этих допустимых значений удовлетворяют условию задачи.
При исходная система примет вид:
Оценим обе части первого уравнения системы. как сумма взаимно обратных положительных величин.
Поэтому последняя система равносильна следующей:
Значит, при исходная система имеет единственное решение (0; 0).
Следовательно, при система имеет единственное решение (-3; 0).
При исходная система примет вид:
Система не имеет решения.
Найти значения параметра t, при которых система имеет два решения.
При x = y исходная система примет вид: Из уравнения найдем допустимые значения параметра t: t = 1; t = 3.
При исходная система примет вид: Из уравнения
найдем допустимые значения параметра t: t = 1; t = 3.
При t = 1 исходная система примет вид: Система не имеет решения при t = 1. Значение t = 1 не удовлетворяет условию задачи.
При t = 3 исходная система примет вид: Прибавим к первому уравнению системы второе уравнение, умноженное на 2. Затем вычтем из первого уравнения второе уравнение, умноженное на 2.
Система примет вид: или
При t = 3 исходная система имеет два решения:
При t = 3 исходная система примет вид: Система не имеет решений при t = 3. Значит, t = 3 не удовлетворяет условию задачи.
При t = 1 исходная система примет вид:
При t = 1 система (исходная) имеет два решения:
Найти значения параметра 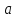
Пусть решение системы, тогда также решение системы.
При 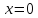
При 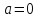
или или три решения.
Значит, 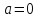
При каких значениях параметра 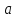
Если решение данного уравнения, то и также является его решением в силу четности функции в левой части уравнения. Следовательно,
При 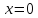
Проверка. При 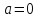
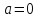
При исходное уравнение примет вид: Левая часть уравнения правая Следовательно, решением уравнения является решение системы: х=0 – единственное решение.
Найти значения параметра при которых система имеет два решения.
При x = y система примет вид:
Допустимое значение параметра 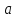
При система примет вид: и не имеет решения.
Проверка: при 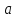
Ответ: 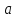
Найти все значения параметра при каждом из которых уравнение имеет единственный корень.
Подставим 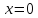
Симметрия в задачах с параметрами
1 И. В. Яковлев Материалы по математике MathUs.ru Симметрия в задачах с параметрами Симметрия одно из ключевых понятий математики и физики. Вы знакомы с геометрической симметрией фигур и вообще различных объектов природы. Однако математические представления о симметрии распространяются гораздо шире: оказывается, например, что можно говорить о симметрии некоторых уравнений. Так, уравнения, выражающие фундаментальные физические законы, обладают определённой симметрией; это свидетельствует о том, что симметрия принадлежит к числу наиболее глубоких свойств нашего мира. Что же такое симметрия уравнений? Мы не будем сейчас стремиться к строгим определениям и ограничимся следующим описанием. Если при некотором преобразовании переменных уравнение не меняет своего вида («переходит само в себя»), то мы говорим, что это уравнение симметрично относительно данного преобразования 1. Почему бывает важно замечать симметрию уравнений? Дело в том, что если уравнение обладает некоторой симметрией, то такой же симметрией обладают и все его решения. Значит, не решая уравнение и исходя лишь из соображений симметрии, мы можем заранее предвидеть некоторые свойства его решений! Допустим, например, что требуется найти такие значения параметра, при которых уравнение имеет заданное число решений. Тогда, заметив симметрию данного уравнения, мы сможем получить необходимые условия на параметр, и останется лишь проверить, какие из найденных условий являются достаточными. Задача 1. (МГУ, мехмат, 1990 ) Найдите все значения параметра b, при которых уравнение имеет единственное решение. b b tg(cos ) + 1 = 0 (1) Решение. Обратите внимание, что уравнение (1) не меняет своего вида при замене на (ведь и cos чётные функции). Иными словами, уравнение (1) симметрично относительно преобразования (то есть относительно отражения в начале координат). Следовательно, данной симметрией будут обладать и решения нашего уравнения. Именно, если 0 корень уравнения (1), то и число 0 будет его корнем; иначе говоря, решения уравнения (1) расположены симметрично относительно нуля. Вместе с тем, в задаче требуется, чтобы решение было только одно. Единственная возможность корнем уравнения (1) является нуль, и только он. В самом деле, если уравнение имеет ненулевое решение, то всего решений будет как минимум два. Подставляя = 0 в уравнение (1), получим b tg = 0, откуда b = ctg 1. () 1 Мы сейчас не делаем различия между уравнениями и системами уравнений. Да его, в общем-то, и нет; например, система уравнений f(, y) = 0, g(, y) = 0 равносильна уравнению f(, y) + g(, y) = 0. Поэтому, говоря о симметрии уравнений, мы имеем в виду также и симметрию систем уравнений. 1
2 Это необходимое условие на b (только при таком b наше уравнение может иметь нулевое решение). Теперь вопрос в том, является ли это условие достаточным; то есть, окажется ли при b = ctg 1 нулевое решение и в самом деле единственным, или же уравнение (1) будет иметь и другие корни помимо нуля. Для выяснения достаточности условия () подставим данное значение b в уравнение (1): Перепишем это следующим образом: ctg 1 ctg 1 tg(cos ) + 1 = 0. tg(cos ) tg 1 = 1 + tg 1. () Тангенс является возрастающей функцией на интервале ( π ; π ). Косинус, являющийся аргументом тангенса, принимает значения из отрезка [ 1; 1], а этот отрезок находится внутри интервала ( π ; π ). Следовательно, справедливо неравенство tg(cos ) tg 1, то есть левая часть уравнения () не превосходит 1. В то же время правая часть () не меньше 1, и равенство возможно лишь в том случае, когда обе они равны 1, то есть при = 0. Итак, мы показали, что условие () является достаточным: при b = ctg 1 уравнение (1) имеет единственное (нулевое) решение. Ответ: b = ctg 1. Задача. (МГУ, химический ф-т, 00 ) Найти все значения параметра a, при каждом из которых уравнение имеет единственное решение a + 5a + a + = sin π Решение. Обозначим b = a + 5a + a. Имеем: 9 ( ) + b + = sin π π π + +. () Оказывается, данное уравнение не меняет своего вида при замене на (это отражение в точке = 1). В самом деле, посмотрим, как преобразуются выражения с переменной при преобразовании : sin π π ( ) ( )( ) = ( ); sin π( ) = cos π + sin π. π( ) = sin ( π π ) ( π π ) = Итак, уравнение () симметрично относительно преобразования. Следовательно, если 0 корень уравнения (), то и 0 также будет его корнем. Поэтому единственным решением уравнения () может быть только неподвижная точка преобразования : = = 1. Подставляя = 1 в уравнение (), получим: + b + = + +,
3 откуда b = 0. Это необходимое условие единственности решения уравнения (), и теперь надо выяснить, является ли оно достаточным. Подставляем b = 0 в уравнение (): 9 ( ) + = sin π π +, или 1+( 1) = ( π sin + π ). (5) Левая часть уравнения (5) неотрицательна, а правая часть неположительна. Поэтому равенство возможно лишь в том случае, когда обе части одновременно равны нулю, то есть при = 1. Тем самым показано, что при b = 0 уравнение () в самом деле имеет единственное решение = 1. Остаётся найти соответствующие значения параметра a: Ответ: a = 0, 5± 1. a + 5a + a = 0 a(a + 5a + 1) = 0 a = 0, 5 ± 1 Задача. Найти все значения a, при которых уравнение. имеет единственное решение a = a (6) Решение. Легко видеть, что уравнение (6) не меняет своего вида при преобразовании 1 (такое преобразование называется инверсией). Следовательно, наряду с решением 0 имеется также решение 1 0, и поэтому единственным решением уравнения (6) может быть лишь неподвижная точка нашего преобразования: = 1 = ±1. Подставляя = 1 в уравнение (6), получим a a + = 0; тут корней нет. Подставляя = 1 в уравнение (6), получим a a = 0, то есть a = 1 или a =. Это необходимые условия на параметр a. Проверим, достаточны ли они. Пусть a = 1. Тогда уравнение (6) примет вид: + 1 = (7) Если 0, то левая часть (7) не меньше (как сумма двух взаимно обратных положительных чисел), а правая часть не больше (поскольку к единице прибавляется дробь, не превосходящая единицу). Следовательно, равенство (7) возможно лишь тогда, когда обе части одновременно равны, то есть при = 1. Итак, a = 1 годится: в этом случае уравнение (6) действительно имеет единственное решение = 1. Пусть теперь a =. Уравнение (6) примет вид: =. (8)
4 Рассмотрим функцию в левой части уравнения (8): f() = Мы видим, что f(1) =, и теперь нас интересует, является ли = 1 единственным корнем уравнения f() =. Нетрудно понять, что это не так. В самом деле, имеем f() > и в то же время f() = или 0 1. Тогда + 1 = 6 + = 0 = 1. Условие > выполнено, так что = 1 корень уравнения (11).
5 1. 0; = 6 Из второго уравнения (1) мы видим, что y 1. Поэтому для правой части первого уравнения имеем оценку: y sin 1. В то же время его левая часть: + 1 1, так что равенство в первом уравнении (1) возможно лишь в случае одновременного равенства обеих частей единице, то есть при = 0, y = 1. Пара (0, 1) удовлетворяет также второму уравнению и потому является единственным решением системы (1). Стало быть, значение a = нам подходит. Пусть теперь a = 0. Система (1) примет вид: 1 = y sin, tg + y = 1. Можно указать два решения полученной системы: (0, 1) и (π, 1). Следовательно, значение a = 0 не годится. Ответ: a =. Задача 6. (МГУ, филологич. ф-т, 00 ) Найти все a, при которых система y ( a), (y a) (1) имеет единственное решение. Решение. Заметим, что система (1) переходит сама в себя при замене на y и y на. Иными словами, наша система симметрична относительно преобразования (, y) (y, ), которое является отражением координатной плоскости относительно прямой y = (рис. 1). Y (y, ) y = y (, y) y X Рис. 1. Отражение (, y) (y, ) Следовательно, наряду с решением ( 0, y 0 ) система имеет также решение (y 0, 0 ). Поэтому для того, чтобы система (1) имела единственное решение, необходимо, чтобы выполнялось равенство 0 = y 0 (то есть чтобы решением системы служила неподвижная точка преобразования, расположенная на прямой y = ). Полагая в системе y =, получим неравенство ( a) (a + 1) + a 0. (15) Но на прямой y = должна быть лишь одна точка, являющаяся решением нашего неравенства; поэтому полученное квадратное неравенство (15) должно иметь единственное решение. Значит, дискриминант должен обратиться в нуль: D = (a + 1) a = 0, 6
7 откуда a = 1. Это необходимое условие на параметр, и нужно проверить его достаточность. Подставляем a = 1 в систему (1): ( y + 1, ) + ( y + 1 ) y + 1 0, 16 y + y Сложим неравенства полученной системы: y y + 1 ( 16 0 ) 1 ( + y 1 0. ) Единственным решением данного неравенства будет пара ( 1 ; 1 ). Она же будет единственным решением системы (1) при a = 1, что мы и хотели проверить. Ответ: a = 1. Во всех рассмотренных задачах наблюдалась симметрия относительно какого-то одного преобразования. Однако симметрий может быть несколько! Задача 7. Найти все значения a, при которых система + y = 1, + y = a (16) имеет ровно четыре решения. Решение. Система не меняет своего вида, если заменить на, или y на y, или поменять местами и y. Иными словами, система (16) симметрична относительно преобразований (, y) (, y), (, y) (, y), (, y) (y, ). Следовательно, если ( 0, y 0 ) решение системы (16), то решениями будут также пары ( 0, y 0 ), ( 0, y 0 ), ( 0, y 0 ), (y 0, 0 ), ( y 0, 0 ), (y 0, 0 ), ( y 0, 0 ). Все эти пары получаются в результате последовательных отражений исходной точки относительно координатных осей и прямых y = ± (рис. ). Y y = X y = Рис.. Симметрия решений системы (16) 7
8 Таким образом, если система (16) имеет решение, расположенное вне прямых = 0, y = 0, y = ±, то у этой системы будет не менее восьми решений. Ровно четыре решения система может иметь лишь в том случае, когда она имеет решение, расположенное на одной из прямых = 0, y = 0, y = ± (тогда восьмиугольник вырождается в квадрат, рис. ). Y Y y = y = X X y = y = Рис.. Система (16) имеет ровно четыре решения Если = 0 или y = 0, то из системы (16) получаем a = 1. Если же y = ± (то есть y = ), то из системы (16) получаем a = 1. Это необходимые условия на параметр. Остаётся проверить, достаточны ли они. Пусть a = 1. Тогда система (16) примет вид: + y = 1, + y (17) = 1. Делаем замену u =, v = y : u + v = 1, u + v = 1. Решаем эту систему и убеждаемся, что у неё ровно два решения: u = 1, v = 0 и u = 0, v = 1. Эти две пары (u, v) дают ровно четыре пары (, y) решений системы (17): (1, 0), ( 1, 0), (0, 1), (0, 1). Таким образом, значение a = 1 годится. Пусть теперь a = 1. Тогда система (16) примет вид: + y = 1, + y = 1. (18) Снова делаем замену u =, v = y : u + v = 1, u + v = 1. Эта система имеет единственное решение u = v = 1, которое даёт ровно четыре решения системы (18): ( 1, ) ( 1, 1, ( 1 ), 1, ) ( 1, 1, ) 1. Следовательно, значение a = 1 также является подходящим. Ответ: a = 1 или a = 1. 8
И. В. Яковлев Материалы по математике MathUs.ru. Область значений функции

Графический способ решения уравнений с параметром
Преобразуем исходную систему
Изобразим решение системы на плоскости \((xOy)\). Отметим, что уравнение \(y=p+3+x\) задает семейство прямых для различных значений параметра \(p\) и углом наклона \(k=1\).
Точки пересечения семейства прямых \(y=p+3+x\) с графиком функции \(x=\frac<1> <4>(y-1)^2-1\) и удовлетворяющих \(y≥1\) будут решениями системы.
Зеленым покажем область, в которой наша система имеет решения. Синие точки – возможные решения при различных \(p\).
Теперь проанализируем график на количество решений при различных значениях параметра. Для этого сначала найдем такие \(p\), при которых прямые \(y=p+3+x\) будут касаться параболы, просто решив систему
с учетом, что корень должен быть всего один (дискриминант равен 0).
Таким образом, прямая \(y=x+3\) будет касательной к графику функции \(x=\frac<1> <4>(y-1)^2-1\) в точке \((0;3)\). При \(p=0\) будет одно решение системы.
Теперь обратим внимание, что при \(p>0\) семейство прямых \(y=p+3+x\) не будет пересекать параболу, а значит и не будет решений.
Через точку параболы \((-1;1)\) проходит прямая при \(p=-1\). Значит при \(p∈[-1;0)\) систему будет иметь два решения.
И, наконец, при \(p 0\) решений нет;
Найти количество решений уравнения \(a*<2>^<2x>-(1+a) <2>^
Сделаем замену \(t=2^x\), \(t>0\) получим уравнение:
И построим на координатной плоскости \((tOy)\) графики функций
Для удобств запишем все в виде системы:
И так, первое уравнение системы задает семейство парабол (при \(a≠0\)), которые пересекают ось \(t\) в точках \((0;0)\) и \((1;0)\). Это следует из того, что \(0=at^2-at\), т.е. либо \(a=0\), либо \(t^2-t=0\) ⇔ \(
Обратите внимание, что ни одна парабола при любом значении \(a≠0\) не может целиком лежать выше или ниже оси \(t\). Это следует из равенства \(0=at^2-at\) при любом значении \(a\). то есть вершины семейства парабол с \( a>0\) лежат ниже оси \(t\), а вершины парабол с \(a
Ответ: Теперь глядя на рисунок 19 заметим, что при \(a>1\) полупрямая \(y=t-1\) и парабола \(y=at^2-at\) будут иметь две общие точки, а значит и два решения. При \(a=1\) будет только одно решение. При \(a∈(0;1)\) не будет общих точек. При \(a=0\) у нас будет пересечение двух прямых \(y=0\) и \(y=t-1\) – одна общая точка. И при \(a