Метод циглера никольса настройки параметров регулятора
Настройка ПИД-регулятора. Метод Циглера-Никольса.
В предыдущей статье мы разобрались с принципом работы ПИД-регулятора (ссылка). Теперь, как и обещал, рассмотрим основные методы настройки и подбора его коэффициентов ) Вообще, по большому счету, при использовании ПИД-регулятора необходимо построить модель всей системы в целом и математически вычислить необходимые значения коэффициентов. Так делать правильно. Но, естественно, так никто не делает 🙂
На самом деле, математический расчет коэффициентов задача далеко не тривиальная, требует глубоких знаний теории автоматического управления, поэтому и используются другие, упрощенные, методы настройки.
Наиболее часто использующимся методом настройки коэффициентов является метод Циглера-Никольса. Заключается он в следующем…
Метод Циглера-Никольса.
Собственно, на этом практическая часть метода заканчивается. Из полученного коэффициента K рассчитываем пропорциональный коэффициент ПИД-регулятора:
А из него получаем и остальные:
Метод довольно прост, но применить его можно далеко не всегда. Если честно, мне еще ни разу не приходилось настраивать регулятор таким образом. Но тем не менее, этот метод является основным и, по большому счету, единственным широко известным. Просто подходит не всем и не всегда.
Что же делать, если метод Циглера-Никольса не сработал? Тут придет на помощь “аналитический” метод настройки 🙂
Опять же обнуляем все коэффициенты и начинаем увеличивать пропорциональный. Но теперь не ждем появления колебаний, а просто фиксируем поведение системы для каждого значения коэффициента (отличным вариантом будет построение графика величины, которую необходимо стабилизировать, для каждого значения коэффициента). Если видим, что, например, система очень медленно выходит на нужное значение, увеличиваем пропорциональный коэффициент. Система начинает сильно колебаться относительно нужной величины? Значит, коэффициент слишком велик, уменьшаем и переходим к настройке других составляющих.
Понимая, как работает ПИД-регулятор в целом, и представляя, как должна работать настраиваемая система, можно довольно-таки быстро и точно настроить коэффициенты регулятора. Особенно, если есть возможность построить графические зависимости и визуально следить за поведением системы.
Вот некоторые правила, которые могут помочь при настройке ПИД-регулятора:
Кстати, стоит добавить, что не всегда необходимо использовать все три составляющие ПИД-регулятора, порой хватает пропорциональной и дифференциальной, например (ПД-регулятор). В общем, все сводится к тому, что для каждой системы необходим свой собственный подход при настройке и использовании ПИД-регулятора.
На этом на сегодня все, возможно, как-нибудь рассмотрим практическую реализацию ПИД-регулятора!
ПИД-регулятор. Методика настройки
2020-07-10 

ПИД-регулятор (пропорционально-интегрально-дифференциальный) — устройство, с обратной связью, применяемое в автоматических системах управления для поддержания заданного значения параметра. Благодаря своей универсальности они широко применяются в различных технологических процессах.
Выходной сигнал регулятора определяется по следующей формуле:
u (t) = P + I + D = Kp e (t) + Ki ∫e (t) dt + Kd de (t)/dt
u (t) – выходной сигнал регулятора;
P – пропорциональная составляющая;
I – интегрирующая составляющая;
D – дифференцирующая составляющая;
Ki — интегральный коэффициент
Kd – дифференциальный коэффициент
e (t) – ошибка рассогласования
Задачи ПИД-регулятора в системах АСУ ТП
Основная задача ПИД регулятора состоит в поддержании определенного значения параметра технологического процесса на заданном уровне. То есть говоря простым языком, задача ПИД-регулятора заключается в том, чтобы учитывая полученные значения с датчиков (обратная связь) воздействовать на объект управления, плавно подводя регулируемое значение к заданным уставкам. Применение ПИД регуляторов целесообразно, а зачастую и единственно возможно в процессах, где необходима высокая точность переходных процессов, непрерывный контроль и регулирование заданных параметров, недопустимы значительные колебания в системе.
Сравнение ПИД –регулятора с позиционным регулированием
В системах АСУ ТП наибольшее распространение получили два типа регуляторов – двухпозиционный и ПИД.
Двухпозиционный регулятор наиболее простой в использовании и широко распространенный.
Данный тип регулятора сравнивает значение входной величины с заданным параметром уставки. Если значение измеренной величины ниже заданного значения уставки, регулятор включает исполнительное устройство, при превышении заданного значения, исполнительное устройство выключается. Для предотвращения слишком частого срабатывания устройства, в следствии колебаний системы и следовательно изменении значений, задается минимальный и максимальный порог срабатывания — гистерезис, или по другому зона нечувствительности, мертвая зона, дифференциал. Например, нам необходимо поддерживать температуру в 15°С. Если гистерезис задан 2°, то регулятор будет включать нагрев при 14°С и отключать соответственно при 16°С.
Так или иначе, при таком типе регулирования происходят незатухающие колебания, частота и амплитуда которых зависит от параметров системы. Поэтому данный метод обеспечивает хороший результат в системах, обладающих инерционностью и малым запаздыванием. В частности, такой метод широко применяется при регулировании температуры в нагревательных печах.
В отличии от двухпозиционного с помощью ПИД-регулятора удается свести колебания системы к минимуму, благодаря тому, что при таком методе регулирования учитываются различные значения системы — фактическая величина, заданное значение, разность, скорость. Это позволяет стабилизировать систему и добиться повышения точности в десятки раз по сравнению с двухпозиционным методом. Конечно, здесь многое зависит от правильно подобранных коэффициентов ПИД регулятора.
Составляющие ПИД-регулятора
В стандартном ПИД-регуляторе есть три составляющие и каждая из них по своему воздействует на управление.
Пропорциональная — P (t) = Kp * e (t)
Учитывает величину рассогласования заданного значения и фактического. Чем больше отклонения значения, тем больше будет выходной сигнал, то есть пропорциональная составляющая пытается компенсировать эту разницу.
Однако пропорциональный регулятор не способен компенсировать полностью ошибку рассогласования. Всегда будет присутствовать так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. При увеличении коэффициента пропорциональности Kp статическая ошибка уменьшается, но могут возникнуть автоколебания и снижение устойчивости системы.
Интегральная – I (t) = Ki ∫e (t) dt
Интегральная составляющая используется для устранения статической ошибки. Она складывает значение предыдущих ошибок рассогласования и компенсирует их, можно сказать, что учится на предыдущих ошибках. То есть ошибка рассогласования умножается на коэффициент интегрирования и прибавляется к предыдущему значению интегрирующего звена. При выходе системы на заданный режим, интегральная составляющая перестает изменяться и не оказывает какого-либо серьезного воздействия на систему. Физически интегральная составляющая представляет задержку реакции регулятора на изменение величины рассогласования, внося в систему некоторую инерционность, что может быть полезно для управления объектами c большой чувствительностью.
Дифференциальная – D (t) = Kd de (t)/dt
Дифференциальная составляющая учитывает скорость изменения регулируемой величины, противодействуя предполагаемым отклонениям, вызванными возмущениями системы или запаздыванием. И чем больше будет величина отклоняться от заданной, тем сильнее будет противодействие, оказываемое дифференциальной составляющей. То есть она предугадывает поведение системы в будущем. При достижении величины рассогласования постоянного значения дифференциальная составляющая перестает оказывать воздействие на управляющий сигнал.
На практике какая-либо из составляющих может не использоваться (чаще всего Д-дифференциальная) и тогда мы получаем П-регулятор, ПИ-регулятор.
Методика настройки ПИД-регулятора
Выбор алгоритма управления и его настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.
В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.
В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.
Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип — проволочные, навитые на керамические трубки.
Требования: поддержание температуры по зонам печи +/- 5С.
МЕТОДИКА:
Настройка пропорциональной компоненты (Xp)
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры;
∆t — период колебаний температуры.
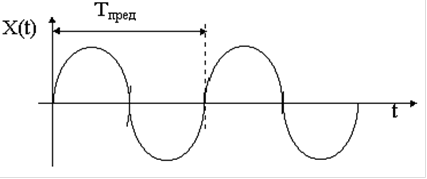
Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.
3. Используя полученные параметры рассчитываем Ти и Тд.
| Зона пропорциональности | Коэффициент передачи | Постоянная времени интегрирования | Постоянная времени дифференцирования | |
| П-регулятор | 2*PBs | 0.5*Xp | ||
| ПИ-регулятор | 2.2*PBs | 0.45*Xp | 0.83*ʌТ | |
| ПИД-регулятор | 1.67*PBs | 0.6*Xp | 0.5*ʌТ | 0.125*ʌТ |
Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.
Вывод
Благодаря достаточно высоким получаемым результатам ПИД-регуляторы нашли широкое применение в системах автоматического управления.
При этом важно подчеркнуть, что настройка ПИД-регулятора является процессом довольно трудоемким и требует определенных знаний и индивидуального подхода для различных объектов управления.
Tech Elements
Радиоэлектроника и телекоммуникации
б) затем коэффициент пропорциональности регулятора Кп постепенно увеличивают, пока при некотором значении этого коэффициента Кп пред в системе не установятся устойчивые колебания с периодом Т пред. ( см. рис.4)
в) далее рассчитываются и устанавливаются параметры регулятора на основе следующих соотношений:
Для П- регулятора Кп= 0,5 Кп пред;
Для ПИ- регулятора Кп= 0,45 Кп пред, Ти= Т пред/1,2;
Для ПИД- регулятора Кп= 0,6 Кп пред, Ти= Т пред/2, Тд= Т пред/8.
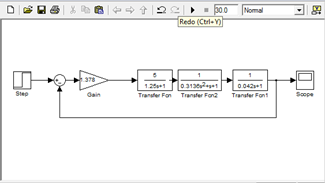
)Выведем Систему На границу устойчивости.
Рисунок 5. Структурная Схема система при критическом коэффициенте передачи.
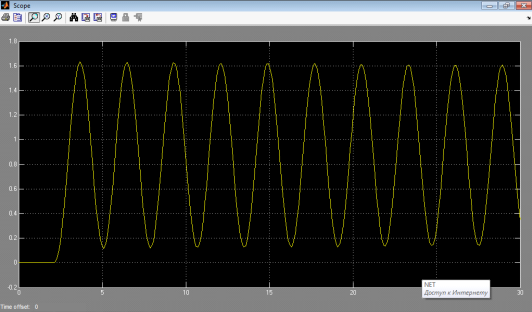
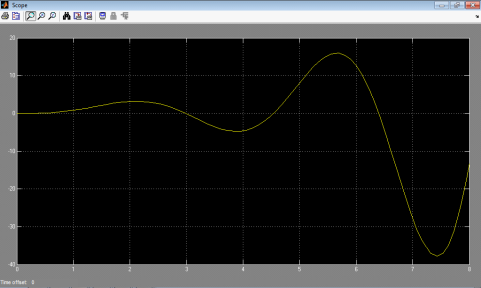
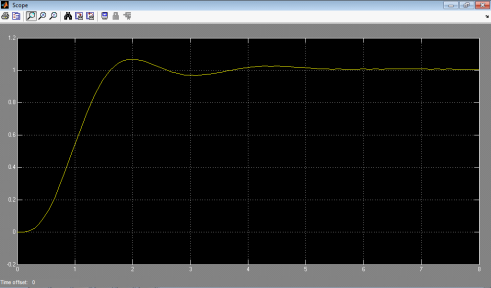
Рисунок 6. Переходный процесс Системы при критическим коэффициенте передачи.
)Найдем параметры регуляторов.
Из (рис 6) Следует, что время колебания Тпред=3,9с.
Регулятор на «П» структуре нам не подходит т.к он не обеспечивает нулевую статическую ошибку.
Для ПИ- регулятора Кп= 0,62 ; Ти= 3,25с;
Для ПИД- регулятора Кп= 0,826; Ти= 1,95; Тд= 0,4875.
Рисунок 7. Переходный процесс Системы с «ПИ» регулятором.
Рисунок 8. Переходный процесс Системы с «ПИД» регулятором.
Другие стьтьи в тему
Метод Циглера – Никольса настройки параметров регулятора 5
Типовой П – регулятор 7
Типовой ПИ – регулятор 8
Типовой ПИД – регулятор 9
Список использованных источников 27
Введение
Автоматическое управляющее устройство состоит измерительного устройства, элемента сравнения и регулятора. Регулятор, на вход которого поступает сигнал ошибки, формирует управляющие воздействие непосредственно на объект управления в соответствии с заданным алгоритмом управления. Алгоритм управления описывается передаточной функцией.
Выбор алгоритма управления является основной задачей в процессе проектирования. Синтез регуляторов, дающих наилучшие показатели качества управления, как правило, представляют собой сложную задачу. С другой стороны, в виду сложности и реализация таких регуляторов часто оказывается экономически неоправданной. Во многих случаях для автоматизации производственных процессов используются простейшие и наиболее распространенные типы линейных регуляторов.
Пропорционально – интегральный регулятор. Управляющие воздействие, формируемое на выходе регулятора содержит пропорциональную и интегральную составляющие. Достоинством ПИ-регулятора является то, что он устраняет статическую ошибку, обусловленную возмущением. Однако введение интегральной составляющей в регулятор ухудшает условия устойчивости.
Пропорционально-интегрально– дифференциальный регулятор. Управляющие воздействие, формируемое регулятором, содержит, кроме пропорциональной и интегральной составляющих, третью составляющую, пропорциональную производной сигнала ошибки. В большинстве случаев с помощью правильного построенного ПИД-регулятора удается выполнить все требования к системе. Согласно статистики более 90% промышленных регуляторов представляют собой именно ПИД-регуляторы.
Метод Циглера – Никольса настройки параметров регулятора
Этот метод, предложенный в 1943г., относится к эмпирическим и основан на использовании данных, полученным экспериментально на реальном объекте.
В данном случае, используется реакция объекта на ступенчатое изменение управляющего воздействия.
Простой метод настройки ПИД регулятора

Есть два похода к настройке ПИД регулятора. Первый – синтез регулятора, то есть вычисление параметров регулятора на основании модели системы. Данный метод позволяет очень точно рассчитать параметры регулятора, но он требует основательного погружения в ТАУ.
Второй метод – ручной подбор параметров (коэффициентов). Это метод научного тыка проб и ошибок. Берем готовую систему, меняем один (или сразу несколько коэффициентов) регулятора, включаем регулятор и смотрим за работой системы. В зависимости от того, как ведет себя система с выбранными коэффициентами (недо/пере регулирование) опять меняем коэффициенты и повторяем эксперимент. И т. д. Ну, такой метод имеет право на жизнь, главное представлять как изменение того или иного коэффициента повлияет на систему (что бы не действовать совсем наугад).
Есть более «оптимизированный» метод подбора коэффициентов – метод Зиглера–Никольса.
Сразу скажу, что метод работает не для любой системы, результаты получаются не самыми оптимальными. Но, зато, метод очень простой и годится для базовой настройки регулятора в большинстве систем.
Суть метода состоит в следующем:
1. Выставляем все коэффициенты (Kp, Ki, Kd) в 0.
2. Начинаем постепенно увеличивать значение Kp и следим за реакцией системы. Нам нужно добиться, чтобы в системе начались устойчивые колебания (вызванные перерегулированием). Увеличиваем Kp, пока колебания системы не стабилизируются (перестанут затухать).
3. Запоминаем текущее значение Kp (обозначим его Ku) и замеряем период колебаний системы (Tu).
Все. Теперь используем полученные значения Ku и Tu для расчета всех параметров ПИД регулятора по формулам:
Kp = 0.6 * Ku
Ki = 2 * Kp / Tu
Kd = Kp * Tu / 8
Готово. Для дискретных регуляторов нужно еще учесть период дискретизации – T ( умножить на Ki та Т, разделить Kd на Т).
Еще раз повторюсь, ТАУ изучать нужно, синтез регуляторов рулит, описанный метод годится для базовой настройки, подходит не для всех систем и т. д. Но данный метод очень простой, и вполне годится для «бытового» уровня.