Методы оценки параметров систем уравнений

Методы оценки параметров одновременных уравнений

Коэффициенты структурной модели могут быть оценены разными методами в зависимости от вида системы одновременных уравнений.

Наиболее из них распространены следующие методы оценки:

· ­ косвенный МНК (КМНК);

· ­ двухшаговый МНК (ДМНК);

· ­ трехшаговый МНК (ТМНК);

· ­ метод максимального правдоподобия с полной информацией;

· ­ метод максимального правдоподобия при ограниченной информации.

Косвенный и двухшаговый МНК рассматриваются как традиционные методы оценки коэффициентов структурной модели.

КМНК применяется для идентифицируемой системы одновременных уравнений, а ДМНК используется для оценки коэффициентов сверхидентифицируемой модели.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК, но при большом числе уравнений системы этот метод приводит к достаточно сложным процедурам вычислений.

Дальнейшим развитием ДМНК является ТМНК. Этот метод пригоден для оценки параметров всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективен ДМНК.

Процедура применения косвенного метода наименьших квадратов (КМНК) предполагает выполнение следующих этапов:

­ преобразование структурной модели в приведенную форму;

­ для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты δ_ij.

­ коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

При непосредственном применении традиционного МНК к каждому уравнению структурной формы результаты могут сильно отличаться от результатов применения КМНК.

Если система сверхидентифицируема, то КМНК не даст однозначных оценок параметров структурной модели и поэтому он не используется. В этом случае можно использовать разные методы, среди которых наиболее распространен ДМНК.

Основная идея ДМНК – получение на основе приведенной формы модели для сверхидентифицируемого уравнения теоретических значений эндогенных переменных, содержащихся в правой части уравнения.

Затем, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.

Источник

Методы оценивания параметров систем одновременных уравнений

Оценивание структурных параметров систем одновременных уравнений связано с рядом трудностей, являющихся следствием специфических свойств данного вида моделей. В общем случае эндогенные переменные и ошибки в них коррелированы, поэтому применение метода наименьших квадратов к уравнениям системы (5.5) нежелательно, так как полученные оценки параметров будут смещенными и несостоятельными [2, 191.

Процесс оценивания параметров системы эконометрических уравнений следует начинать только в том случае, когда система прошла проверку на идентифицируемость.

В зависимости от результатов этой проверки могут быть использованы различные методы оценивания, среди которых выделим следующие |2, 10, 19, 28]:

Далее рассмотрим подробнее косвенный, двухшаговый и трехшаговый методы наименьших квадратов, считающиеся традиционными для оценивания параметров структурной формы систем эконометрических уравнений и обладающие сравнительно невысокой сложностью вычислений. Методы максимального правдоподобия являются достаточно сложными с вычислительной точки зрения и в настоящем учебнике рассматриваться не будут.

Следует отметить, что при анализе результатов оценивания параметров структурной формы необходимо очень внимательно отнестись к проблеме интерпретации. Подход, аналогичный модели множественной регрессии, здесь неприемлем. Например, рассмотрев первое уравнение системы (5.7) как уравнение множественной регрессии, можно сказать, что коэффициент а_и показывает среднее изменение величины у_< с увеличением х_< на единицу при фиксированном значении у₂. Однако в соответствии со вторым уравнением системы (5.7) изменение у_< влечет за собой изменение г/₂, т.е. у₂ не может быть постоянным в данном случае. Если из экономического содержания модели смысл структурных коэффициентов неясен, то не следует стремиться дать им формальное объяснение. В отношении интерпретации коэффициентов приведенной формы подобных проблем не возникает.

Источник

Методы оценки систем одновременных уравнений

Непосредственное применение обычного метода наименьших квадратов для оценки уравнений системы (в структурной форме) нецелесообразно, так как в системах одновременных уравнений нарушается важнейшее условие регрессионного анализа — экзогенность факторов. Это приводит к тому, что оценки параметров будутсмещёнными и несостоятельными.

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

косвенный метод наименьших квадратов;

двухшаговый метод наименьших квадратов;

трехшаговый метод наименьших квадратов;

метод максимального правдоподобия с полной информацией;

метод максимального правдоподобия при ограниченной информации.

Рассмотрим кратко сущность каждого из этих методов.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.

Структурная модель преобразовывается в приведенную форму модели.

Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты .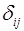

Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).

Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 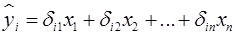и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

все уравнения системы сверхидентифицируемы;

система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

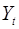
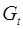
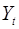
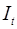
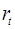
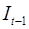
Для примера, рассмотренного в предыдущем параграфе, необходимо применить именно двухшаговый метод наименьших квадратов. Но можно сделать следующее замечание. Если из модели исключить тождество дохода, число эндогенных переменных модели снизится на единицу – переменная станет экзогенной. А число предопределенных переменных модели не изменится, т.к. из модели будет исключена эндогенная переменная , но ее место займет переменная . В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной от эндогенной переменной (которая зависит только от предопределенных переменных) и предопределенной переменной . Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования уравнения на идентификацию.

Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легко реализуемы.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андерсоном и Н.Рубиным.

В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Источник

Методология оценивания параметров систем уравнений

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили следующие методы оценивания коэффициентов структурной модели:

Косвенный и двухшаговый методы наименьших квадратов рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легко реализуемы. Косвенный метод наименьших квадратов (КМНК) применяется для идентифицируемой системы одновременных уравнений, а двухшаговый метод наименьших квадратов (ДМНК) используется для оценки коэффициентов сверхидентифицируемой модели. Остальные перечисленные методы также используются для сверхидентифицируемых систем уравнений.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации является метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т. Андерсоном и Н. Рубиным. Математическое описание метода дано, например, в работе Дж. Джонстона. Несмотря на значительную популярность данного метода, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Источник

Методы оценки параметров систем уравнений

Основная цель эконометрического моделирования – изучение взаимосвязей между переменными, описывающими экономические объекты. При моделировании простых экономических объектов используются отдельные изолированные уравнения парной или множественной регрессии. Для описания сложных экономических систем, включающих несколько экономических объектов, используются не отдельные уравнения, которых недостаточно для объяснения их функционирования, а системы уравнений. Возникает необходимость оценивания систем уравнений. Для этой цели в эконометрике разработаны специальные методы исследования и оценивания. Методы оценивания зависят от типа системы уравнений. Если исследуемая система включает независимые уравнения (система независимых уравнений), то каждое уравнение может рассматриваться самостоятельно, и для оценки его параметров, при условии выполнения всех предпосылок Гаусса – Маркова, можно использовать обычный метод наименьших квадратов (МНК, ordinary least squares method, OLS), при гетероскедастичном возмущении – метод взвешенных наименьших квадратов (weighted least squares method, WLS), при гетероскедастичности и/или автокорреляции – обобщенный метод наименьших квадратов (ОМНК, generalized least squares method, GLS) [1].

Если взаимосвязь уравнений объясняется только корреляцией их случайных возмущений (влиянием «одной экономической среды» на формирование переменных уравнения), то такая система называется системой внешне не связанных уравнений (Seemingly Unrelated Regression, SUR). Оценка параметров SUR выполняется в рамках обобщенного метода наименьших квадратов (ОМНК), применяемого к специальным образом составленной спецификации модели [2].

Если система состоит из набора взаимосвязанных уравнений, и одни и те же переменные в одних уравнениях являются эндогенными, а в других – регрессорами, то такие системы называют системами одновременных уравнений, СОУ (Simultaneous equations). СОУ чаще остальных систем используется в эконометрических исследованиях. Для оценки параметров СОУ используются: косвенный метод наименьших квадратов (КМНК, indirect least squares method, ILS), двухшаговый метод наименьших квадратов (ДМНК, two stage least squares method, 2SLS), которые позволяют решить проблему эндогенности переменных, возникающую при оценке структурных параметров системы. Повысить точность ДМНК-оценок структурных параметров можно в рамках трёхшагового метода наименьших квадратов (ТМНК, three stage least squares method, 3SLS), учитывающего взаимодействие уравнений в системе [3]. Рассмотрим методы оценки параметров СОУ на примере следующей модели [4]:

(1)

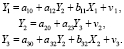
Вектор эндогенных переменных системы (1) включает элементы: Y1 – объем продукции (в тыс. штук); Y2 – количество работающих (в тыс. человек); Y3 – стоимость основных фондов (в млн злотых), вектор экзогенных переменных: X1 – использованное сырьё (в тыс. тонн); X2 – инвестиции (в млн злотых). Данные за 11 лет приведены в табл. 1.

Источник