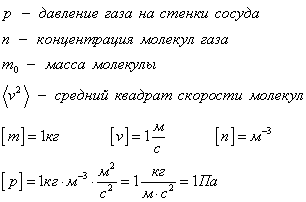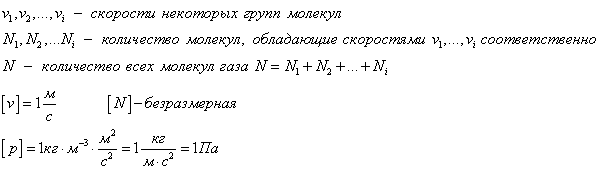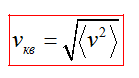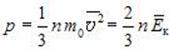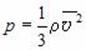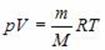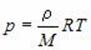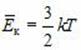Микро и макро параметры мкт
Урок 14. Микро- и макроскопические параметры системы. Идеальный газ. Основное уравнение МКТ.
Молекулярная физика, описывая состояние вещества, оперирует макро- и микропараметрами.
К макропараметрам вещества относятся:
· Давление вещества р (Па)
· Масса вещества m (кг)
· Объем вещества V (м 3 )
· Температура вещества Т (К)
К микропараметрам относятся:
· Масса отдельной молекулы m0 (кг)
· Скорость молекулы v (м/c)
Моль – количество вещества, в котором содержится столько же молекул, сколько их в 12 граммах углерода.
Число Авогадро 

Закон Авогадро: в равных объемах различных газов при одинаковых условиях всегда содержится одинаковое число молекул.
Относительная атомная масса Аr это отношение массы одного атома m0 к одной двенадцатой массы атома углерода mС :
Относительная атомная масса указана в таблице элементов Д. И. Менделеева

Относительная молекулярная масса 
Молярная масса М(кг/моль) – это масса 1 моль данного вещества.
Пример: Найдем молярную (молекулярную) массу карбоната кальция СаСО3
Чтобы найти молекулярную массу кальцита нужно суммировать все атомные массы, умноженные на коэффициенты. В нашей формуле только возле Оксигена есть коэффициент 3, потому найти молярную массу будет просто:
1. Умножаем атомную массу Оксигена на коэффициент: 16 на 3 = 48.
Помните при решении задач :
Формулы массы одной молекулы 

Формулы количества вещества γ (моль) :
Формулы количества молекул N:

Плотность вещества ρ (кг/м 3 ):
Температура
Температура Т (К) – это мера средней кинетической энергии теплового движения молекул.
Английский ученый Кельвин предложил температурную шкалу, на которой за начало отсчета принят абсолютный нуль (0 К). Эта шкала была названа абсолютной шкалой температур, или шкалой Кельвина, а температура измеренная по этой шкале, получила название абсолютной температуры и обозначается буквой Т. Шкала Кельвина не имеет отрицательных температур, потому что температуры ниже 0 К не существует, она не имеет физического смысла.
В быту используют шкалу Цельсия. На этой шкале за начала отсчета принят 0 0 С – температура, при которой тает лед. Температуру измеренную по шкале Цельсия обозначают t 0 C.
Связь между шкалами Цельсия и Кельвина:
Цена деления на шкале Кельвина такая же, как и цена деления на шкале Цельсия, поэтому изменение температуры на обеих шкалах одинаково:
Большинство законов молекулярно-кинетической теории описывает процессы в идеальном газе.
Идеальный газ – газ, удовлетворяющий трем условиям:
1. Молекулы – материальные точки
2. Потенциальной энергией взаимодействия можно пренебречь
3. Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным. Близким к идеальному является газ под низким давлением и при высокой температуре. Воздух при нормальных условиях 
Основное уравнение МКТ идеального газа связывает макропараметры и микропараметры.
Давление идеального газа:

Физический смысл абсолютной температуры:
Формулы средней квадратичной скорости молекул:
Смесь газов
Рассмотрим пример: Пусть в первом сосуде имеется газ с давлением 




Здесь: 

Учебники
Журнал “Квант”
Общие
Микро- и макропараметры системы
Содержание
Атомы и молекулы, взаимодействую друг с другом, образуют разнообразные вещества (системы). Если число частиц невелико (десятки, сотни), то мы имеем микросистему. Если число частиц системы во много раз больше (миллионы и более), то такую систему называют макросистемой. Например, газ, состоящий из очень большого числа молекул — это макросистема. Большое число частиц системы приводит к появлению у нее новых свойств, которыми отдельные частицы не обладают. Например, давление газа есть результат непрерывного действия всех молекул на стенки сосуда, хотя не каждая молекула сталкивается со стенками. Для описания состояния макросистемы вводят параметры, которые называются параметрами состояния. Различают микропараметры и макропараметры состояния.
Микропараметры — это параметры, характеризующие отдельную частицу. Например, масса молекулы, ее скорость, энергия.
Макропараметры
Макропараметры — это параметры, характеризующие систему в целом. Например, объем V, давление p, средняя скорость молекул \(
\left\langle \upsilon \right\rangle\), температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.
Давление р — скалярная физическая величина, равная отношению силы F к значению площади S площадки, на которую эта сила действует\[
p = \dfrac\]. Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В Си единица давления 1 Н/м 2 = 1 Па (Паскаль). Внесистемные единицы измерения — 1 мм.рт.ст и 1 атмосфера. Нормальное давление равно одной физической атмосфере. 1 физическая атмосфера = 1 атм = 760 мм.рт.ст, 1 техническая атмосфера = 1 ат = 736 мм.рт.ст. 1 мм.рт.ст. = 133Па.
Концентрация молекул n — это число молекул N в единице объема, т.е. \(
Температура — скалярная физическая величина, характеризующий степень нагретости тела.
По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС). За 1 ºС принята одна сотая промежутка от температуры плавления льда (0 ºС) до температуры кипения воды (100 ºС).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т.е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия.
где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (ºС).
Средние скорости молекул газов
Движение молекул газа подчиняется законам статистической физики. В каждый момент времени скорости отдельных молекул могут значительно отличаться друг от друга, но их средние значения одинаковы и при расчетах используются не мгновенные скорости отдельных молекул, а не которые средние значения. Различают среднюю арифметическую \(
\left\langle \upsilon \right\rangle\) и среднюю квадратичную \(
\left\langle \upsilon_
Средняя квадратичная скорость хаотического движения молекул
\left\langle \upsilon^2 \right\rangle\) — средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости\[
\left\langle \upsilon^2 \right\rangle \ne \left\langle \upsilon \right\rangle^2\].
См. также
Идеальный газ
Рассмотрим свойства газов на основе МКТ. Для этого введем физическую модель идеального газа, в которой приняты следующие допущения:
1) размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принимать за материальные точки;
2) силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;
3) молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами механики.
Таким образом, идеальным называется газ, в котором можно пренебречь собственным объемом молекул и межмолекулярным взаимодействием (кроме столкновений).
При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. Например, водород, кислород при нормальных условиях в атмосфере можно рассматривать как идеальные газы.
При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.
Основное уравнение МКТ идеального газа — это уравнение, связывающее микро- и макропараметры идеального газа. Одно из этих уравнений имеет вид:
где p — давление газа (Па); n — концентрация молекул (м –3 ); m0 — масса одной молекулы газа (кг); 〈v 2 〉 — среднее значение квадрата скорости молекул (м/с 2 ). Это уравнение называют еще уравнением Клаузиуса.
Давление можно выразить через среднюю кинетическую энергию молекул\[
\left\langle E_k \right\rangle = \dfrac
p = \dfrac 23 n \cdot \left\langle E_k \right\rangle. \quad (2)\)
Вывод основного уравнения
Температура – мера средней кинетической энергии молекул
Можно провести следующий эксперимент. Взять сосуды с разными газами. Определить предварительно их объемы, массы и рассчитать число молекул (по формуле \(
N = \dfrac mM \cdot N_A\)), затем поместить сосуды в тающий лед. После наступления теплового равновесия определить давление p и рассчитать отношение \(
\dfrac
\dfrac
\dfrac
p = \dfrac
где p — давление газа (Па); n — концентрация молекул (м –3 ); T — температура газа (К); k — постоянная Больцмана, равная 1,38·10 –23 Дж/К.
Сравнивая выражения (3) и (2), получаем
\( \dfrac 23 n \cdot \left\langle E_k \right\rangle = n \cdot k \cdot T, \) или \(
\left\langle E_k \right\rangle = \dfrac 32 k \cdot T. \)
Данная формула верна для расчёта средней энергии поступательного движения молекулы или для расчёта средней кинетической энергии одноатомной молекулы. Если учитывать, наряду с поступательным движением и вращение молекулы, то средняя кинетическая энергии молекулы с жесткой связью (без колебании атомов в молекуле) будет равна
\left\langle E_k \right\rangle = \dfrac i2 k \cdot T, \)
где i — степень свободы. Для одноатомного газа (например, инертные газы) i = 3, для двухатомного — i =5.
Температура – это величина, характеризующая среднюю кинетическую энергию поступательного движения молекул идеального газа:
Эта формула позволяет установить физический смысл абсолютной температуры Т. Этот макроскопический параметр характеризует среднее значение кинетической энергии хаотического теплового движения одной молекулы в состоянии термодинамического равновесия. Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом.
Так как абсолютная температура не может равняться нулю, то и средняя энергия теплового движения молекул то же не может равняться нулю, т.е. молекулы находятся в постоянном движении.
II. Молекулярная физика
Тестирование онлайн
Идеальный газ
Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.
Параметры состояния газа
Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.
Основное уравнение молекулярно-кинетической теории
Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.
Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.
Основное уравнение мкт имеет вид

Средний квадрат скорости молекул

Средняя квадратичная скорость vкв молекул это квадратный корень из среднего квадрата скорости
Средняя кинетическая энергия молекул

Можно вывести формулы

Температура
Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.
Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.


Связь между температурами по шкале Цельсия и по шкале Кельвина
Микро и макро параметры мкт
Микро- и макропараметры состояния газа
Основное уравнение МКТ
Температура. Абсолютная температура
Связь температуры со средней кинетической энергией молекул вещества
Микро — и макропараметры состояния газа
Система, состоящая из большого числа молекул, называется макросистемой. Макросистема, отделенная от внешних тел стенками с постоянными свойствами, после длительного промежутка времени приходит в равновесное состояние. Это состояние можно описать рядом параметров, называемых Параметрами состояния. Различают Микропараметры и Макропараметры состояния.
К микропараметрам состояния можно отнести следующие физические величины: массу M0 молекул, их скорость, среднюю квадратичную скорость молекул, среднюю кинетическую энергию молекул, среднее время между соударениями молекул, длину их свободного пробега и др. Это такие параметры, которые можно отнести и к одной молекуле макросистемы.
Макропараметры состояния характеризуют только равновесную систему в целом. К ним относятся объем V, давление P, температура T, плотность , концентрация N, внутренняя энергия U, электрические, магнитные и оптические параметры. Значения этих параметров могут быть установлены с помощью измерительных приборов.
Молекулярно-кинетическая теория идеального газа устанавливает соответствие между микропараметрами и макропараметрами газа.
Таблица. Mикропараметры состояния
| Параметр | Обозначение | Единицы в СИ |
| Масса молекулы | M0 | Кг |
| Скорость молекулы | 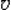 | М/c |
| Cредняя квадратичная скорость движения молекул | 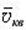 | М/c |
| Средняя кинетическая энергия поступательного движения | 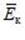 | Дж |
Таблица. Макропараметры состояния
| Параметр | Обозначение | Единицы в СИ | Способ измерения (косвенный способ) |
| Масса газа | M | Кг | Весы |
| Объем сосуда | V | М3 | Мерный цилиндр с водой; измерение размеров и расчет по формулам геометрии |
| Давление | P | Па | Манометр |
| Температура | T | К | Термометр |
| Плотность | | Кг/м3 | Измерение массы, объема и расчет |
| Концентрация | N | 1/м3 = м-3 | Измерение плотности и расчет с учетом молярной массы |
| Cостав (молярная масса и соотношение количеств ) | М1, М2, безразмерная | Приготовление газа смешением заданных масс или объемов |
Основное уравнение молекулярно-кинетической теории идеального газа
Это уравнение связывает макропараметры системы – давление P и концентрацию молекул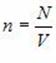
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки.
Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой.
Учитывая связь между концентрацией молекул в газе и его плотностью ( = Nm0), можно получить еще одну форму основного уравнения МКТ идеального газа:
Температура. Абсолютная температура
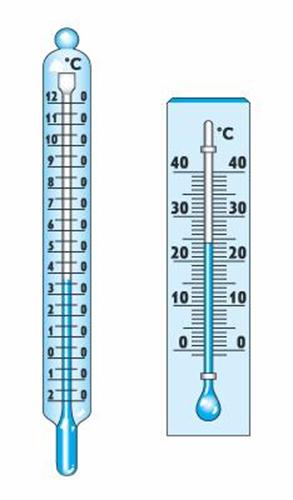
Рис. 2. Жидкостные термометры
При контакте двух макросистем, каждая из которых находится в равновесии, например, при открывании крана между двумя теплоизолированными сосудами с газом или контакте их через теплопроводящую стенку, равновесие нарушается. Через большой промежуток времени в частях объединенной системы устанавливаются новые значения параметров системы. Если говорить только о макропараметрах, то выравниваются температуры тел.
Понятие «температура» было введено в физику в качестве физической величины, характеризующей степень нагретости тела не по субъективным ощущениям экспериментатора, а на основании объективных показаний физических приборов.
Термометр – прибор для измерения температуры, действие которого основано на взаимно-однозначной связи наблюдаемого параметра системы (давления, объема, электропроводности, яркости свечения и т. д.) с температурой (рис. 2).
Считается, что если этот вторичный параметр (например, объем ртути в ртутном термометре) при длительном контакте с одним телом и при длительном контакте с другим телом одинаков, то это значит, что равны температуры этих двух тел. В экспериментах по установлению распределения молекул по скоростям было показано, что это распределение зависит только от степени нагретости тела, измеряемой термометром. В современной статистической физике характер распределения частиц системы по энергиям характеризует ее температуру.
Для калибровки термометра необходимы тела, температура которых считается неизменной и воспроизводимой. Обычно это температура равновесной системы лед – вода при нормальном давлении (0 °С) и температура кипения воды при нормальном давлении (100 °С).
В СИ температура выражается в кельвинах (К). По этой шкале 0 °С = 273,15 К и 100 °С = 373,15 К. В обиходе используются и другие температурные шкалы.
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния:
Где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная, 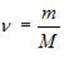
Пользуясь уравнением состояния, можно выразить один параметр через другой и построить график первого из них, как функции второго.
Графики зависимости одного параметра от другого, построенные при фиксированных температуре, объеме и давлении, называют соответственно Изотермой, Изохорой и Изобарой.
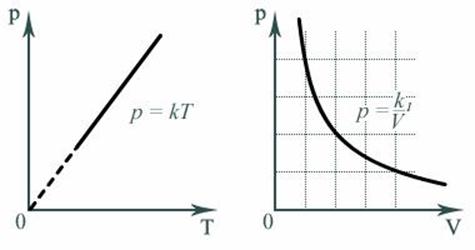
Например, зависимость давления P от температуры T при постоянном объеме V и постоянной массе M газа – это функция 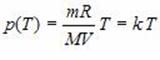
Зависимость давления P от объема V при постоянной массе M газа и температуре T выражается так:
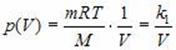
Где K1 – постоянный числовой множитель. График функции 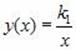
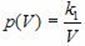
Связь температуры со средней кинетической энергией молекул вещества
Количественное соотношение между температурой T (макропараметром) системы и средней кинетической энергией 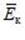
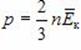
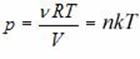
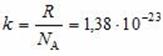
Средняя кинетическая энергия молекул идеального газа пропорциональна температуре газа. Если молекулы газа образованы двумя, тремя и т. д. атомами, то доказывается, что это выражение связывает только энергию поступательного движения молекулы в целом и температуру.
С учетом этого соотношения на уровне микро — и макропараметров макросистемы можно утверждать, что в Состоянии теплового равновесия двух систем выравниваются температуры и в случае идеального газа средние кинетические энергии молекул.