Модели с сосредоточенными и распределенными параметрами
Модели с сосредоточенными и распределенными параметрами
Модели бывают статистическими и логико-математическими, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов на изучаемый объект, явление или процесс. Логико-математические модели делятся на три класса: 1) модели с сосредоточенными параметрами; 2) модели с сосредоточенно-распределенными параметрами, т. е. переходные; 3) модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.
Математическая модель с сосредоточенными параметрами– это модель системы, поведение которой описывается обыкновенными дифференциальными уравнениями.
Данная модель включает в себя переменные, которые зависят только от времени и не зависят от координат. Математическая модель с сосредоточенными параметрами имеет вид системы обыкновенных дифференциальных уравнений.
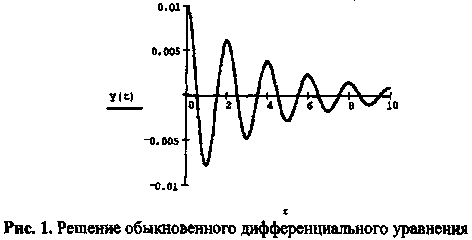
Решением дифференциального уравненияназывается n раз дифференцируемая функция x(t), удовлетворяющая уравнению во всех точках своей области
определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие, например: потребовать, чтобы решение принимало в данной точке данное значение.
Пример. Дифференциальное уравнение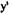 
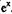
= у (вместе с начальным условием у(0) =1) задает экспоненту: у(х) = 
. Если х обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов.
Математическая модель с распределенными параметрами– модель системы, описываемая дифференциальными уравнениями в частных производных.
Модель содержит переменные, зависящие от пространственных координат, и представляет собой систему дифференциальных уравнений в частных производных или систему интегро-дифференциальных уравнений. Важной характеристикой дифференциальных уравнений является их порядок, т. е. порядок старшей производной, которая входит в эти уравнения.
Пример. Уравнение колебания струны. Данное уравнение имеет вид:
Классификация математических моделей.
Ввиду разнообразия применяемых математических моделей, их общая классификация затруднена. В литературе обычно приводят классификации, в основу которых положены различные подходы. Один из таких подходов связан с характером моделируемого процесса, когда выделяют детерминированные и вероятностные модели. Наряду с такой широко распространенной классификацией математических моделей существуют и другие.
Классификация математических моделей на основе особенностей применяемого математического аппарата. В ней можно выделить следующие их разновидности.
Математические модели с сосредоточенными параметрами.
Математические модели с распределенными параметрами.
Моделями этого типа описываются процессы диффузии, теплопроводности, распространения волн различной природы и т. п. Эти процессы могут быть не только физической природы. Математические модели с распределенными параметрами широко распространены в биологии, физиологии и других науках. Чаще всего в качестве основы математической модели применяют уравнения математической физики, в том числе и нелинейные.
Математические модели, основанные на экстремальных принципах.
Общеизвестна основополагающая роль принципа наибольшего действия в физике. Например, все известные системы уравнений, описывающие физические процессы, могут быть выведены из экстремальных принципов. Однако и в других науках экстремальные принципы играют существенную роль.
Основной принцип классификации математических моделей
В качестве основного принципа классификации математических моделей часто используют области их применения. При таком подходе выделяются следующие области применения:
технические приложения, в том числе управляемые системы, искусственный интеллект;
жизненные процессы (биология, физиология, медицина);
большие системы, связанные с взаимодействием людей (социальные, экономические, экологические);
гуманитарные науки (языкознание, искусство).
(Области применения указаны в порядке, соответствующем убыванию уровня адекватности моделей).
Виды математических моделей: детерминированные и вероятностные, теоретические и экспериментальные факторные. Линейные и нелинейные, динамические и статические. непрерывные и дискретные, функциональные и структурные.
По форме представления математических моделей различают инвариантную, алгоритмическую, аналитическую и графическую модели объекта проектирования.
Классификация математических моделей
В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:
Поясним это на примерах.
Дескриптивные (описательные) модели. Например, моделирование движения кометы, вторгшейся в Солнечную систему, производится с целью предсказания траектории ее полета, расстояния, на котором она пройдет от Земли, и т.д. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на движение кометы, что-то в нем изменить.
Оптимизационные модели используются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения.
Многокритериальные модели. Нередко приходится оптимизировать процесс по нескольким параметрам одновременно, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, нужно организовать питание больших групп людей (в армии, детском летнем лагере и др.) физиологически правильно и, одновременно с этим, как можно дешевле. Ясно, что эти цели совсем не совпадают, т.е. при моделировании будет использоваться несколько критериев, между которыми нужно искать баланс.
Игровые модели могут иметь отношение не только к компьютерным играм, но и к весьма серьезным вещам. Например, полководец перед сражением при наличии неполной информации о противостоящей армии должен разработать план: в каком порядке вводить в бой те или иные части и т.д., учитывая и возможную реакцию противника. Есть специальный раздел современной математики — теория игр, — изучающий методы принятия решений в условиях неполной информации.
Численный эксперимент выясняет, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на компьютере, совпадают с экспериментальными с заданной степенью точности.
По сравнению с натурным экспериментом математическое моделирование имеет следующие преимущества:
• экономичность (сбережение ресурсов реальной системы);
• возможность моделирования гипотетических, т.е. не реализованных в натуре объектов;
• возможность реализации режимов, опасных или трудновоспроизводимых в натуре (критический режим ядерного реактора, работа системы противоракетной обороны);
• возможность изменения масштаба времени;
• легкость многоаспектного анализа;
• большая прогностическая сила вследствие возможности выявления общих закономерностей;
• универсальность технического и программного обеспечения проводимой работы.
Достоверность численной модели.
Поиск новых средств доказательства достоверности численных результатов представляет собой насущную проблему при разработке современных вычислительных технологий. Один из наиболее перспективных подходов заключается в применении методов интервальной математики, которые позволяют получить численное решение в виде интервала с гарантированными границами. В настоящее время в этой области достигнут значительный успех, для многих сложных задач получены численные решения. При этом сама процедура вычислительного процесса одновременно является доказательством существования (и даже единственности) решения.
Трудности прямого применения таких методов в ряде случаев заключаются в том, что интервал неопределенности исходных данных слишком широк и, как следствие, результат имеет весьма большую погрешность. В частности, такая ситуация возникает при учете возможности ошибок программирования при решении нелинейных задач математической физики, поскольку это решение связано с разработкой сложных программ при отсутствии аналитических отладочных примеров.
14. Понятие динамической системы
Динамическими системами называют класс задач, представленных задачами Коши для обыкновенных дифференциальных уравнений (ОДУ) или систем таких уравнений.
Теория динамических систем и специфические численные методы наиболее развиты для динамических систем, описываемых ОДУ (более простые уравнения).
Задача Коши для системы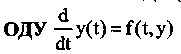
состоит в отыскании неиз-
вестной векторной функции y(t), включающей несколько (L) неизвестных функций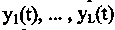
, для начального условия у(0) = С.
Соответственно числу компонент векторной функции y(t) должно быть поставлено L начальных условий. Исходя из физического смысла такой постановки задачи можно, не теряя общности, полагать, что дифференциальные уравнения содержат производные по аргументу t, являющемуся временем, и, соответственно, описывают динамику во времени различных физических параметров y(t). Поэтому задачи Коши для таких моделей называют динамическими системами, а для их изучения центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде
, а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргументtвходит в графики лишь параметрически (см. рис. 1).
Классические примеры моделей динамических систем, описываемых системами ОДУ: нелинейный осциллятор, динамика популяций (Вольтерра), электронный генератор автоколебаний (Ван дер Поля), турбулентная конвекция жидкости (Лоренца), химическая реакция с диффузией (Пригожина). Все примеры являются типичными динамическими системами и содержат производные по времени t, описывая динамику различных физических параметров.
15. Модели с сосредоточенными и распределенными параметрами
Модели бывают статистическими и логико-математическими, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов на изучаемый объект, явление или процесс. Логико-математические модели делятся на три класса: 1) модели с сосредоточенными параметрами; 2) модели с сосредоточенно-распределенными параметрами, т. е. переходные; 3) модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.
Данная модель включает в себя переменные, которые зависят только от времени и не зависят от координат. Математическая модель с сосредоточенными параметрами имеет вид системы обыкновенных дифференциальных уравнений.
Решением дифференциального уравнения называется n раз дифференцируемая функция x(t), удовлетворяющая уравнению во всех точках своей области
определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие, например: потребовать, чтобы решение принимало в данной точке данное значение.
Пример. Дифференциальное уравнение
= у (вместе с начальным условиему(0) =1) задает экспоненту: у(х) =
. Если х обозначает время, то эта функцияописывает рост популяции в условиях неограниченности ресурсов.
Модель содержит переменные, зависящие от пространственных координат, и представляет собой систему дифференциальных уравнений в частных производных или систему интегро-дифференциальных уравнений. Важной характеристикой дифференциальных уравнений является их порядок, т. е. порядок старшей производной, которая входит в эти уравнения.
Пример. Уравнение колебания струны. Данное уравнение имеет вид:
Математические модели объектов с сосредоточенными параметрами
При моделировании объектов с сосредоточенными параметрами математическая модель представляет собой систему обыкновенных дифференциальных и (или) алгебраических уравнений.
Используют три следующие основные модели объектов с сосредоточенными параметрами.
1. Модель в форме задачи Коши (явная форма) определяет система обыкновенных дифференциальных уравнений (ОДУ) вида
В более лаконичной векторной форме система ОДУ (3.1) записывается в виде
где X — (ях1)-вектор фазовых переменных с компонентами хр х2. хп; F(X, t) — вектор-функция той же размерности; Х° — аналогичный вектор начальных условий.
2. Модель в дифференциально-алгебраической форме (полуявная форма) имеет вид
где Y= (yv у2. у ) — (т х 1)-вектор алгебраических переменных, G(X, Y) — (тх 1)-вектор-функция.
3. Модель в дифференциально-алгебраической форме (неявная форма) определяет система уравнений
где G — ((п +т) х 1)-вектор-функция.
Математические модели вида (3.2) — (3.4) строят на основе компонентных и топологических уравнений объекта проектирования. Уравнения, описывающие состояния элементов объекта, называют компонентными уравнениями, а уравнения, задающие взаимосвязи элементов объекта, — топологическими. Таким образом, математическая модель объекта с сосредоточенными параметрами представляет собой совокупность компонентных и топологических уравнений этого объекта.
Математические модели объектов с распределенными параметрами
Математическими моделями объектов с распределенными параметрами, используемыми в САПР, являются, в основном, краевые задачи для дифференциальных уравнений в частных производных (ДУЧП). Фазовыми переменными в этих уравнениях могут быть температура (если речь идет о задаче теплопроводности, например), величина механического напряжения (в задаче анализа на прочность) и т.д.
Различают стационарные и нестационарные краевые задачи для ДУЧ П. В стационарной краевой задаче решение не зависит от времени. В качестве независимых переменных в такой задаче чаще всего используют пространственные переменные х, у, Z- В нестационарной краевой задаче решение меняется во времени. В качестве независимых переменных в данном случае используются пространственные переменные х, у, z и время /.
Как в стационарной, так и в нестационарной краевых задачах для ДУЧП должны быть заданы граничные условия — значения фазовых переменных и (или) их некоторых функций на границе моделируемого объекта. Различают граничные условия первого, второго и третьего рода.
где к и q — как правило, константы; п — нормаль к поверхности объекта.
Граничные условия третьего рода представляют собой так называемые уравнения баланса вида f^—, К 1 = 0. Примером является урав-
нение теплового баланса на границе области:
где X — коэффициент теплопроводности материала объекта; а — коэффициент теплообмена объекта с окружающей средой; Тс — температура окружающей среды; Г — температура на границе; п — нормаль к поверхности объекта.
В нестационарных задачах кроме краевых условий должны быть заданы начальные условия — значения фазовых переменных и (или) их некоторых функций внутри объекта в начальный момент времени:
Пример 1. Двумерная стационарная краевая задача имеет вид
где L — дифференциальный оператор, например оператор Лапласа
_+_; Р — часть уравнения, независящая от V
Требуется определить значения фазовой переменной Кв области, определяемой ее границей Г. Задачу иллюстрирует рис. 3.1.
Рис. 3.1. Двумерный объект с заданными граничными условиями
Пример 2. Двумерную нестационарную краевую задачу определяет выражение
где L — дифференциальный оператор, например оператор
Требуется определить значения фазовой переменной Кв области, определяемой ее границей Г на заданном интервале времени[0; /к].
Поскольку непосредственное решение на ЭВМ краевых задач для ДУЧП невозможно, используют дискретные аналоги этих уравнений, приводящие, в общем случае, к системе нелинейных алгебраических уравнений (НАУ). Известны два основных метода сведения краевой задачи для ДУЧП к системе НАУ — метод конечных разностей (МКР) и метод конечных элементов (МКЭ).
Что нужно знать для успешного проектирования печатных плат
В статье рассматриваются некоторые важные вопросы проектирования двухслойных печатных плат, и даются проверенные практикой рекомендации. Кроме того, обсуждаются особенности анализа схем с сосредоточенными и распределенными элементами.
Многие потребительские изделия, микроконтроллеры и IoT-приложения построены на двухслойных печатных платах. Возможности двухслойной печатной платы ограничены – как правило, на ней трудно осуществить разводку BGA-корпуса ПЛИС или выводов современного микроконтроллера. В этой статье мы обсудим правила проектирования для плат не самого высокого уровня.
На рисунке 1 в качестве примера двухслойной печатной платы показана Arduino Uno – платформа для разработки на базе микроконтроллера ATmega.
Рис. 1. Пример недорогой печатной платы Arduino Uno
Arduino Uno очень «живуча» – она всегда заработает, каким бы правилом проектирования вы ни воспользовались, что, к сожалению, расхолаживает разработчиков. Можно смело утверждать, что разработка на основе Arduino являет собой образец того, как не следует проектировать, чтобы затем не переделывать схему.
Две проблемы, которые необходимо избежать
Схема определяет лишь используемые в ней компоненты и способ их соединения, но не позволяет установить целостность сигнала или питания.
Межсоединения могут ухудшить рабочие характеристики изделия. К наиболее частым и сложным проблемам целостности сигналов и питания относятся перекрестные помехи, обусловленные взаимной индуктивностью между контурами сигнала и обратного тракта (помехи по земле) и коммутационный шум на шинах питания, вызванный в переходных процессах током большой амплитуды. На рисунке 2 показан результат измерения помехи по земле платы Arduino Uno при одновременном включении и выключении нескольких выходных каскадов цифровых микросхем.
Рис. 2. Результаты измерения помехи по земле на плате Arduino Uno при замыкании и размыкании нескольких ключей
При физическом проектировании платы, включающем создание топологии, необходимо соблюдать основные правила проектирования, чтобы уменьшить влияние этих двух проблем. Без тщательного анализа, который должен выполнять каждый инженер, можно только следовать некоторым общим рекомендациям, позволяющим уменьшить риск появления указанных проблем. Мы рассмотрим несколько рекомендаций, которые не гарантируют полный успех, но позволяют снизить риски возникновения отказов.
Совет 1. Ширина сигнального проводника должна быть равной 6 мил, ширина питающих проводников – 20 мил, а диаметр отверстий – 13 мил.
Указанные размеры являются минимальными, и их может реализовать любой производитель при наименьшей цене. Выбор самых узких элементов обеспечивает самую высокую плотность трассировки. Проводник шириной 1 мил (0,025 мм) проводит постоянный ток величиной 1 А; при этом его температура заметно не повышается. Сопротивление такого проводника составляет 80 мОм/дюйм при толщине медного покрытия с удельной массой 1 унция/кв. фут. В большинстве приложений сопротивление проводника печатной платы является приемлемым, даже если его величина составляет 1 Ом. Поскольку длина рассматриваемого сигнального проводника составляет 12 дюймов, потери не играют существенной роли, пока ширина полосы пропускания не превысит 1 ГГц.
Характеристический импеданс проводника шириной 6 мил при использовании стандартной двухслойной платы толщиной 62 мил достигает 150 Ом. Если длительность фронта достаточно мала или длина межсоединений настолько велика, что требуется согласование нагрузки, ее так же легко реализовать для 150‑Ом проводников, как и в случае с 50‑Ом проводниками, если проводники не выходят за пределы платы. При этом рассеяние мощности меньше, чем в случае с 50‑Ом проводниками.
Попробуем установить, насколько большой ток может проходить по проводнику печатной платы, показанной на рисунке 3.
Рис. 3. Образец испытательной платы для определения максимального тока, который могут пропускать проводники разной толщины
По проводнику шириной 20 мил в медном покрытии с удельной массой 1 унция/кв. фут может проходить постоянный ток величиной 3 А, не вызывая заметного повышения температуры. Последовательное сопротивление такого проводника составляет около 25 мОм/дюйм. Сопротивление силового проводника длиной 4 дюйма равно 0,1 Ом, что, как правило, считается незначительной величиной. Если требуется, чтобы по проводникам протекал ток до 10 А, их ширину следует увеличить до 100 мил.
Совет 2. Располагайте компоненты, сигнальные и силовые тракты на слое 1, а обратный заземляющий тракт – на слое 2.
Длину проводника, под которым имеется обратный тракт, можно выбрать сколь угодно большой, не ухудшив рабочие характеристики. Главное – использовать непрерывный обратный тракт под сигнальной линией. Проще всего это сделать, задействовав сплошной заземляющий нижний слой платы.
Таким образом, верхний слой будет отведен под размещение всех компонентов, сигнального и силового трактов, что облегчит последующую отладку при проверке сигнальных проводников. Кроме того, появляется возможность отличить сигнальные проводники от проводников питания по ширине линий.
Совет 3. Размещайте компоненты и сигнальные проводники подальше друг от друга.
Старайтесь размещать сигнальные проводники как можно дальше друг от друга во избежание перекрестных помех. У этих проводников – достаточно большой характеристический импеданс. Поскольку они находятся далеко от слоя с обратным током, между ними возникают перекрестные помехи. Чем меньше расстояние между соседними сигналами, тем эти помехи больше: например, при минимальном интервале перекрестная помеха на ближнем конце достигает 25%.
Совет 4. Изоляционный промежуток для сигнальной линии на заземляющем слое должен быть узким. В противном случае в верхнем слое над зазором устанавливается перемычка.
При проектировании печатной платы следует стремиться к тому, чтобы импеданс обратного тракта каждой сигнальной линии был настолько мал, чтобы обеспечить низкую взаимную индуктивность между соседними парами обратных трактов. При трассировке сигнальной линии по заземляющему слою приходится создавать вокруг нее изоляционный промежуток. Сигнальные проводники, проходящие над этим зазором в обратном тракте, генерируют перекрестные помехи, распространяющиеся на другие сигналы, которые пересекают зазор.
Чтобы минимизировать помехи, следует делать зазоры небольшими, сузив, таким образом, тракт обратного тока. Если же этот зазор велик, в верхний слой добавляется обратный тракт, проходящий над зазором. На рисунке 4 приводятся примеры расположения зазоров в местах их пересечения с проводниками; для обратного тока в верхнем слое установлены перемычки.
Рис. 4. При пересечениях зазоров и проводников используются перемычки для прохождения обратного тока над зазорами
Совет 5. Устанавливайте развязывающие конденсаторы как можно ближе к выводу питания ИС так, чтобы по возможности минимизировать индуктивный контур.
Рекомендуется использовать конденсатор в малом корпусе, выбрав максимальную емкость для этого типоразмера с номинальным напряжением, которое, по меньшей мере, в два раза больше предполагаемого напряжения шины питания. Как правило, в таких случаях применяется многослойный керамический конденсатор емкостью 22 мкФ. Величина его емкости зависит от тока, потребляемого развязываемыми компонентами. Согласно известному эмпирическому правилу, емкость 22 мкФ «справится» с током величиной 22 мА в переходном процесс при минимальном провале напряжения.
Величина емкости не так важна, как минимизация индуктивных контуров между выводами питания и земли ИС и развязывающими конденсаторами. Как правило, с этой целью конденсаторы, установленные как можно ближе к выводам микросхемы, используют короткие широкие проводники силового и заземляющего трактов. На рисунке 5 приведен пример корректного и некорректного использования нескольких конденсаторов в соответствии с этой рекомендацией.
Рис. 5. Пример:
а) корректного и
б) некорректного размещения развязывающих конденсаторов на печатной плате
Совет 6. На всех разъемах по возможности назначайте один обратный тракт каждому цифровому сигналу.
Помехи по земле или коммутационный шум создают несколько сигналов, которые совместно используют один вывод для обратного тока. У многих разъемов – только один или два таких вывода с множеством переключающихся сигналов, в результате чего возникают помехи по земле. Например, у одного заземляющего вывода разъема платы Arduino – 13 цифровых вводов/выводов, которые могут переключаться.
Совет 7. Не следуйте двум известным рекомендациям.
К первой из них относится запрет на использование конденсаторов с разными емкостями 10 мкФ, 1 мкФ и 0,1 мкФ на каждом выводе питания. Мало того, что такое ограничение ничего не дает – в некоторых случаях из-за него возникают дополнительные проблемы. Если на плате имеется место для трех конденсаторов, установите их так, чтобы минимизировать контур индуктивности.
Вторая рекомендация – никогда не использовать медную заливку. Такое ограничение тоже неэффективно и иногда создает ненужные проблемы. Вместо медной заливки используйте проводники для слоя питания. Таким образом можно отслеживать силовые тракты при проверке подключений и отладке. Требование к обеспечению минимального контура индуктивности относится ко всем соответствующим компонентам, начиная с ИС и заканчивая развязывающими конденсаторами. Например, для тока величиной 10 А достаточно, чтобы ширина проводника составляла всего 100 мил.
Что касается заливки для заземления, то для него рекомендуется использовать нижний слой платы с обратными трактами. В случае использования верхней медной заливки в качестве заземления может незаметно произойти разрыв импеданса в обратном тракте.
Не следует думать, что добавление медной заливки, подключенной к заземляющему слою, позволяет уменьшить перекрестные помехи – для их минимизации достаточно обеспечить непрерывные обратные тракты, не перекрывающие друг друга. Медная заливка большой площади между сигнальными проводниками часто становится причиной увеличения перекрестной помехи.
Выводы
Следование этим практическим рекомендациям не гарантирует успеха, но позволяет уменьшить риск возникновения отказа из-за перекрестной помехи или шума на шине питания.
Рис. 6. Двухслойная плата Arduino с микроконтроллером ATmega 32U4, реализованная в соответствии со всеми рекомендациями
В качестве примера следования этим советам на рисунке 6 представлена двухслойная плата Arduino с установленным микроконтроллером ATmega 32U4. Из этого рисунка видно, что в схеме реализованы все упомянутые рекомендации:
Модели с сосредоточенными и распределенными параметрами
Для проектирования двухслойных плат достаточно использовать модели схем с сосредоточенными параметрами. Это простой и удобный способ анализа. К сожалению, он не всегда годится. Рассмотрим примеры использования моделей с сосредоточенными и распределенными параметрами.
Для упрощенного анализа электронных схем применяется модель с сосредоточенными параметрами. Эта методология предполагает, что параметры схемы, к которым относятся сопротивление, емкость и индуктивность, рассматриваются как идеализированные электрические компоненты, соединенные в цепь идеально проводящими проводами. При этом физическими размерами элементов можно пренебречь и независимой переменной является только время (протекающих в них процессов). Однако на практике это не всегда так.
По мере повышения частоты импульсов и уменьшения длительности их фронтов эти элементы равномерно распределяются по подложке вдоль всей длины проводника. Медный проводник и соседствующие с ним диэлектрические материалы становятся линией передачи. Под влиянием поверхностного эффекта ВЧ-ток начинает протекать преимущественно в поверхностном слое, а на качество сигнала влияют зависящие от частоты потери. Проводник печатной платы становится распределенной системой с паразитной индуктивностью и емкостью, которая характеризуется временем задержки и рассеянными отражениями. Описываемое поведение проводника происходит в частотной области.
В [1] показано, что импеданс определяется и во временной, и в частотной областях. Во временной области полное сопротивление резистора R определяется взаимосвязью между напряжением и током (законом Ома), а идеальный конденсатор С – взаимосвязью между запасенным зарядом и напряжением на пластинах. В свою очередь, поведение индуктивности L определяется тем, как быстро изменяется во временной области ток, протекающий через дроссель.
Три элемента R, L, C относятся к категории сосредоточенных компонентов схемы в том смысле, что их свойства можно локализовать в одной точке. Такой подход существенно отличается от свойств идеальной линии передачи, которая тоже состоит из этих трех элементов, но их параметры распределены равномерно по длине диэлектрического слоя. Модель с распределенными элементами применяется, если длина волны становится сопоставимой с физическими размерами схемы, что делает неприменимой модель с сосредоточенными параметрами.
Модель с распределенными элементами используется на высоких частотах, когда длина волны становится короткой. Однако она также применяется в случае очень длинных низкочастотных линий передачи, к которым, например, относятся высоковольтные сети электропитания. В этой модели тремя основными элементами являются распределенная емкость, индуктивность и проводимость (G).
Модель с сосредоточенными параметрами полностью перестает работать, если длина проводника становится больше четверти длины волны сигнала, распространяющегося по проводнику (что соответствует сдвигу фазы синусоидального сигнала на 90°). При этом не только значения, но и свойства компонентов становятся непредсказуемыми. В силу такой зависимости от длины волны модель с распределенными параметрами применяется, главным образом, на высоких частотах. Необходимо понимать, что термины «сосредоточенные» и «распределенные параметры» относятся к длине проводника относительно длины волны сигнала напряжения и токов, проходящих по проводнику.
Системы с сосредоточенными элементами описываются известными дифференциальными уравнениями, поскольку в силу малого размера этих систем (по сравнению с длиной волны) производными по координатам можно пренебречь и рассматривать только производные по времени. С другой стороны, в случае систем с распределенными параметрами требуется учитывать и производные по координатам, и производные по времени, т. е. решить частно-дифференциальные уравнения в частотной области.
Линию передачи можно представить в виде бесконечно большого числа сегментов, в состав которых входят последовательные резистивные и индуктивные, а также шунтирующие емкостные и проводящие элементы (см. рис. 7). Из-за ограниченной скорости распространения в среде сигналу «неизвестно», какая нагрузка находится в конце линии передачи – он «видит» только ее импеданс, который должен быть согласован с импедансом генератора сигналов.
Рис. 7. Линия передачи, состоящая из сегментов с последовательными элементами R-L-C-G
Как формируется электромагнитное поле в линии передачи?
Ответ на этот вопрос нельзя получить даже в Google. По идее, электрическое поле образуется, когда к выходному каскаду ИС прикладывается напряжение. При его изменении возникает всплеск тока, который порождает магнитное поле. Заключенная в сигнале электромагнитная энергия передается со скоростью около половины скорости света (из-за ограничения, обусловленного диэлектрической средой) по линии передачи вдоль проводника. Эта энергия проникает в диэлектрик и рядом расположенные элементы, создавая распределенную систему из паразитных элементов. Электромагнитные поля не ограничиваются многослойной подложкой – в отсутствие соответствующих мер по их нейтрализации излучение становится причиной помех.
Модель системы с распределенными параметрами обеспечивает более высокую точность, но сложнее модели с сосредоточенными параметрами. Выбор модели зависит от точности каждого конкретного приложения, поскольку отсутствует четкая граница по частоте, определяющая использование той или иной модели, хотя на практике такой демаркационной областью является диапазон 100–500 МГц. Одно известное эмпирическое правило гласит, что проводники, длина которых превышает 0,1 длины волны, следует рассматривать как систему с распределенными элементами. Эта область определяется примерно тем участком, где две кривые начинают заметно расходиться (см. рис. 8).
Рис. 8. Анализ сосредоточенных и распределенных элементов линии передачи
Модель с сосредоточенными элементами применяется на сравнительно более высоких частотах в тех случаях, если устройства имеют достаточно малые размеры и изготовлены с помощью соответствующих технологий. Размеры печатных плат со сквозными металлизированными отверстиями превышают размеры эквивалентных плат, собранных с использованием технологии поверхностного монтажа. Размеры гибридных ИС, в которых пассивные элементы выполнены в виде пленок на диэлектрической подложке и используются дискретные полупроводниковые электронные приборы, меньше, чем у аналогичного решения, собранного целиком из дискретных компонентов на печатной плате. Размеры монолитных ИС еще меньше. На достаточно высоких частотах микросхемы, в отличие от печатных плат, можно анализировать в виде модели с сосредоточенными параметрами. То же относится к некоторым радиочастотным устройствам.
Выбор модели анализа особенно важен в случае мобильных устройств, поскольку размеры схем с сосредоточенными элементами, как правило, становятся все меньше. Для иллюстрации разницы между сосредоточенной и распределенной моделями для линии передачи мы сравниваем их на рисунке 8, где показана зависимость напряжения нагрузки от длины линии передачи без потерь.
В зависимости от длительности фронта сигналов модель линии передачи с распределенными элементами начинает отклоняться от упрощенной модели сосредоточенных элементов в диапазоне 0,01–0,1 длины волны сигнала. В рассматриваемой симуляции импеданс нагрузки согласован с импедансом линии передачи, и потому отражениями можно пренебречь.
Хотя модель с распределенными параметрами дает хорошее представление о характеристиках типовой НЧ линии передачи, на высоких частотах необходимо также учитывать потери в проводниках и диэлектриках.
На заметку
В модели с сосредоточенными элементами параметры схемы определяются идеализированными электрическими компонентами, соединенными в цепь идеально проводящими проводами. Считается, что размеры сосредоточенных элементов не влияют на происходящие в них физические процессы.
По мере повышения частоты импульсов и уменьшения длительности их фронтов эти элементы равномерно распределяются по подложке вдоль всей длины проводника.
Электромагнитная энергия проникает в диэлектрик и рядом расположенные элементы, создавая распределенную систему из паразитных элементов.
На высоких частотах применяется модель с распределенными параметрами, когда длина волны становится сравнимой с физическими размерами схемы.
Модель с сосредоточенными элементами полностью прекращает работать, если длина проводника начинает превышать четверть длины волны (что соответствует сдвигу фазы синусоидального сигнала на 90°).
Модель системы с распределенными параметрами обеспечивает более высокую точность, но сложнее модели с сосредоточенными параметрами.
Проводники, длина которых превышает 0,1 длины волны, следует рассматривать как систему с распределенными элементами.
Модель с сосредоточенными элементами применяется для схем на сравнительно более высоких частотах в тех случаях, если устройства имеют достаточно малые размеры и изготовлены с помощью соответствующих технологий.
Размеры схем с сосредоточенными элементами, как правило, становятся меньше.
Модель линии передачи с распределенными элементами начинает отличаться от упрощенной модели сосредоточенных элементов при длине проводников в диапазоне 0,01–0,1 длины волны сигнала.