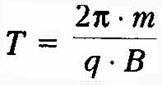момент сил действующих на рамку с током в магнитном поле

Момент сил действующих на рамку с током в магнитном поле

Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.

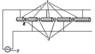
Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.

Момент сил, действующих на рамку с током

Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:

Сила Лоренца

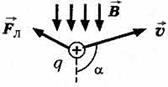
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:

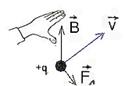
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.

Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.

Теория о магнитном поле

Магнитное взаимодействие токов

Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I₁ и I₂ в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

где: μ₀ – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:

Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Вектор магнитной индукции

Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.

Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

Магнитные свойства вещества

Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:

Магнитный поток. Электромагнитная индукция

Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε_инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.

При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:

При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Движение проводника в магнитном поле

При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

Индуктивность. Самоиндукция. Энергия магнитного поля

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.

Источник

Магнитный момент тока. Рамка с током.

Магнитный момент тока это произведение площади контура, в котором он протекает на силу тока в нем. Магнитный момент направлен перпендикулярно плоскости контура. Это направление можно определить с помощью правила буравчика. Если буравчик вращать по направлению движения тока в контуре, то его поступательное движение укажет направление магнитного момента.

Для наглядности рассмотрим действие магнитного момента тока на примере. Возьмем прямоугольную рамку с током. Поместим ее в постоянное магнитное поле, так чтобы плоскость рамки была параллельна вектору магнитной индукции.

Как известно на проводник, с током помещённый в магнитное поле действует сила Лоренца. Направление, которой можно определить с помощью правила левой руки. Рассматривая действие силы Лоренца на стороны рамки в отдельности можно прийти к выводу, что на них будут действовать силы равные по величине, но противоположные по знаку.

Поскольку эти силы зависят от длинны проводника силы тока в нем и угла между направлением тока и вектором магнитной индукции. А ток в этом контуре протекает один и тот же. Длинна сторон рамки одинакова. И стороны рамки находятся параллельно магнитному полю. Но ток движется в противоположные стороны. Значит и силы будут направлены противоположно.

Две другие стороны рамки не будут взаимодействовать с полем поскольку ток в них течет параллельно силовым линиям поля. Следовательно, исходя из закона Лоренца сила, действующая на них, будет равна нулю.

Далее если мысленно провести вдоль рамки вертикальную осевую линию. То силы, действующие на ее края, будут стремиться ее развернуть. До тех пор пока рамка не примет такое положение, при котором все силы не уравновесятся. При этом рамка повернется своей плоскостью перпендикулярно силовым линия поля.

Таким образом, вращающий момент можно представить в таком виде

где B вектор магнитной индукции
I сила тока в контуре
S площадь рамки с током
sinb угол между вектором магнитной индукции и плоскостью рамки

Источник

Момент сил действующих на рамку с током в магнитном поле

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором и нормалью к площади :

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

Это выражение также можно использовать для определения индукции магнитного поля:

Величину, равную произведению , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

Источник

Момент сил, действующих на контур с током в магнитном поле.

Поместим в однородное магнитное поле с индукцией плоский прямоугольный контур (рамку) с током (рис.9.2).

Рис.9.2. Рамка с током в магнитном поле.

Согласно закону Ампера, на каждый элемент тока рамки действует сила

.

Результирующая всех этих сил, как нетрудно убедиться, создает пару сил и , стремящихся развернуть плоскость рамки перпендикулярно силовым линиям магнитного поля. Если a – короткая сторона рамки, то величина действующей на нее силы будет . Момент пары сил по величине равен:

,

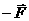
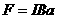
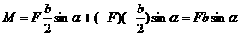
где b – длинная сторона рамки ( — плечо силы F, α – угол между нормалью к плоскости рамки и силовой линией магнитного поля).

Следовательно, можем написать:

,

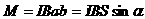
где S = ab – площадь рамки.

Учитывая, что магнитный момент рамки 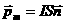, последнюю формулу можно переписать в векторном виде:

Действие магнитного поля на движущийся заряд. Сила Лоренца. Направление силы Лоренца. Траектория движения частицы, влетевшей перпендикулярно направлению магнитного поля и под произвольным углом. Ускорители заряженных частиц.

Сила Лоренца

— сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

.

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).

Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной

и создает центростремительное ускорение равное

В этом случае частица движется по окружности.

.

Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение

тогда радиус окружности

а период обращения заряда в магнитном поле

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

Направление вектора силы Лоренца определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы.

Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля (Рис. 89). Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля , то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F_л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона

, (1)

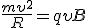
из которого находим

. (2)

Найдем период обращения частицы в магнитном поле

. (3)

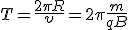
Из этой формулы следует интересный и неожиданный вывод [1] – период вращения частицы в магнитном поле не зависит от ее скорости. Частота вращения выражается формулой

, (4)

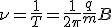
и называется циклотронной частотой.

Ускорители заряженных частиц

·

Рис. 1 Механизм автофазировки

·

Рис. 10 Ускоритель Видероэ (схема)

·

Рис. 11 Резонатор линейного ускорителя (схематический разрез)

Из 12

Ускорители заряженных частиц — устройства для получения заряженных частиц (электронов, протонов, атомных ядер, ионов) больших энергий. Ускорение производится с помощью электрического поля, способного изменять энергию частиц, обладающих электрическим зарядом. Магнитное поле может лишь изменить направление движения заряженных частиц, не меняя величины их скорости, поэтому в ускорителях оно применяется для управления движением частиц (формой траектории). Обычно ускоряющее электрическое поле создаётся внешними устройствами (генераторами). Но возможно ускорение с помощью полей, создаваемых др. заряженными частицами; такой метод ускорения называется коллективным (см. Ускорения заряженных частиц коллективные методы). У. з. ч. следует отличать от плазменных ускорителей, в которых происходит ускорение в среднем электрически нейтральных потоков заряженных частиц (плазмы).

Источник