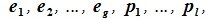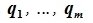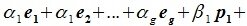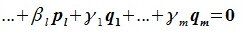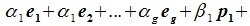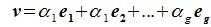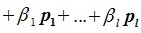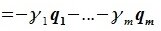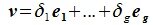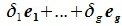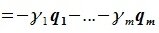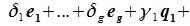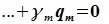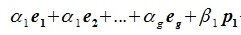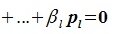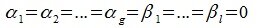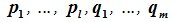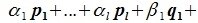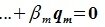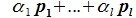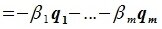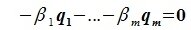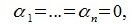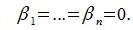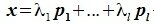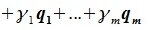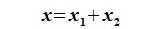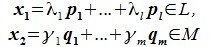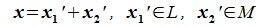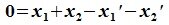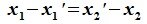Найдите сумму значений параметров a b c при которых матрица принадлежит подпространству

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

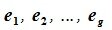
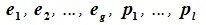
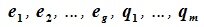
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

Из уравнений (6.4) и (6.5) имеем:

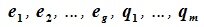
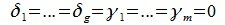
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

В силу линейной независимости базиса подпространства L имеем:

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

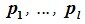
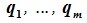
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

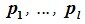
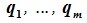
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:

Вычитая (6.19) из (6.17), получим

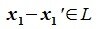
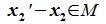
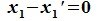
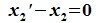
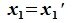
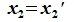
Так как , и L∩M= 0, то и . Следовательно и . ■

Источник

Пересечение и сумма подпространств. Прямая сумма

Пусть дано векторное пространство V, в котором заданы два подпространства U и W.

Определение 1. Пересечением подпространств U и W называется множество UÇW векторов, принадлежащих как подпространству U, так и подпространству W, то есть

Используя теорему 1 § 6, легко проверить, что и сумма, и пересечение подпространств являются подпространствами.

Определение 3. Сумма U+W подпространств U и W называется прямой, если UÇW=<0>.

Прямую сумму подпространств U и V обычно обозначают UÅW.

Теорема 1. Сумма двух подпространств U и W является прямой тогда и только тогда, когда любой вектор z этой суммы единственным образом представим в виде z= x+ y, где xÎU, yÎW.

Достаточность. Пусть представление вектора в виде указанной в теореме суммы единственно. Возьмем любой вектор хÎUÇ W. Тогда хÎU и хÎW, и, заметив, что 0принадлежит любому подпространству, мы можем записать равенство 0 = 0+ 0 = х + (-х), откуда, в силу единственности, следует, что х = 0.

Теорема 2. Размерность суммы двух векторных подпространств равна сумме размерностей этих подпространств без размерности их пересечения, то есть

Если мы докажем, что система (1) линейно независима, то она будет являться базисом суммы подпространств и, следовательно, утверждение теоремы будет доказано. Для этого составим равенство

Перепишем равенство (2) в виде

Из (3) следует, что правая часть этого равенства принадлежит U, так как она выражается через базис подпространства U; вектор в левой части, являясь комбинацией базисных векторов из W, принадлежит W. Но это означает, что и левая, и правая часть равенства (3) является вектором из пересечения UÇW этих подпространств. Поскольку каждый вектор разлагается по базису, разложим левую часть равенства (3) по базису UÇW:

Из (5) мы видим, что линейная комбинация векторов базиса W равна нулю. Следовательно, она тривиальна, в частности, g_m+1=…=g_s=0. Внесем значения этих коэффициентов в равенство (2), тогда получим, что линейная комбинация базисных векторов подпространства U равна нулю и, следовательно, эта комбинация также тривиальна, то есть a₁=…= a_m= b_{m+ 1}= … = b_s= 0. Окончательно имеем, что все коэффициенты в равенстве (2) равны нулю и, следовательно, система (1) линейно независима.

Следствие. dimUÅW = dimU+dimW.

Замечание. Понятие пересечения и суммы подпространств переносятся на любое число подпространств. Так, если даны подпространства U₁,…,U_q, то пересечением их называется множество тех векторов, которые одновременно принадлежат всем рассматриваемым подпространствам, а суммой U₁+…+U_q называется множество всевозможных векторов, представимых в виде x₁+…+x_q, где x₁ÎU₁,…,x_qÎU_q. Если представление вектора суммы в виде x₁+…+x_q единственно, то сумму называют прямой и обозначаютU₁Å…ÅU_q.

Пример. Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:

А = áа₁,а₂ñ, В = áb₁,b₂ñ

Подпространство A + B состоит из векторов вида a + b, где aÎA, bÎB, следовательно, A + B = áа₁,а₂,b₁,b₂ñ. Составим матрицу из координат указанных векторов и найдем её ранг:

Получаем, ранг равен 3, а потому dim(A+B) = 3. В качестве базиса можно взять систему векторов a₁, a₂, b₁.

Подпространство состоит из всех таких векторов x, что

х = α₁a₁ + α₂a₂ = β₁b₁ + β₂b₂.

1. Какая размерность у линейной оболочки, натянутой на векторы (1,0,0,0), (0,1,0,0), (1,1,0,0), (2,2,0,0)?

2. Сколько различных базисов можно выбрать из системы векторов a, b, cдвумерного векторного пространства,если векторы попарно линейно независимы?

x₁-2x₃+4x₄ +1=0 векторное подпространство в R 4 и если да, то какой размерности?

5.Сколько независимых однородных уравнений входит в систему, определяющую двумерное подпространство пятимерного пространства?

6. Какова размерность векторного пространства всех однородных многочленов от двух переменных степени не выше четырех?

7. Из трех векторов а= (1,1), b =(0,1), c = (1,-1) выбран базис. Указать выбранный базис, если известно, что вектор х= (3,1) имеет в этом базисе координаты 1 и 2.

8. Найти матрицу перехода от базиса е₁ = (1,0), е₂ = (0,1) к базису е₁¢ = (1,2), е₂¢ = (3,4).

9. Пусть R₁[x] – пространство многочленов от одного неизвестного х степени не больше единицы, R 2 – арифметическое двумерное пространство. Изоморфизм j из R 2 в R₁[x] переводит базис е₁ = (1,1) и е₂ = (0,1) соответственно в базис х и 1. Найти образ вектора а= (2,4) при этом изоморфизме.

11. Можно ли векторное пространство размерности не меньше 2 представить в виде прямой суммы двух подпространств?

12. Относительно системы векторов е₁,…,е_n известно следующее: каждый вектор линейно выражается через эту систему, и существует некоторый фиксированный вектор, который единственным образом выражается через эту систему. Будет ли такая система образовывать векторный базис?

13. Образуют ли векторное пространство геометрические векторы на плоскости, не параллельные данной прямой?

14. Доказать, что для любого истинного подпространства U векторного пространства V найдется такое подпространство W, что V=UÅW.

15. Доказать, что пересечение всех подпространств векторного пространства, содержащих два данных подпространства, равно сумме этих двух подпространств.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.012 сек.)

Источник

Линейные подпространства

Подмножество L линейного пространства X над полем Р называют линейным подпространством этого пространства, если оно само является линейным пространством относительно введенных в X операций сложения векторов и умножения векторов на числа из поля Р.

Для того чтобы подмножество L линейного пространства X было его линейным подпространством, необходимо и достаточно, чтобы оно было замкнуто относительно операций сложения векторов и умножения векторов на числа из поля Р, т.е. чтобы выполнялись следующие условия:

Действительно, эти условия означают, что операции в линейном пространстве X можно рассматривать и как операции на множестве L. При этом будут верны все аксиомы, кроме третьей и четвертой. Выполнение третьей аксиомы равносильно утверждению, что при выполнении условий 1 и 2 нулевой вектор принадлежит L, а выполнение четвертой означает, что для любого вектора ж € L противоположный вектор —х принадлежит L. Первое из этих утверждений следует из равенства 0 = 0 • ж, где в качестве х можно взять любой вектор в множестве L. Второе утверждение — следствие равенства — х = ( — 1) • х.

Условия 1 и 2 можно объединить в одно условие: для любых векторов множества L их линейная комбинация с произвольными коэффициентами принадлежит L.

Приведем примеры линейных подпространств.

то и векторы a + b и Л а имеют вид

Следовательно, они принадлежат L.

Любое конечномерное линейное пространство порождается конечной системой векторов, например любым своим базисом. Согласно доказанной теореме это верно и для всякого линейного подпространства линейного пространства.

> Действительно, любой базис в L, как и вообще любую линейно независимую систему векторов в X, можно дополнить до базиса линейного пространства X. Если вектор х имеет столбец координат (4.3С), то он имеет представление

Теорема 4-22. Пусть X — конечномерное линейное пространство и в нем задан базис е. Тогда для любого линейного подпространства L в X можно указать такую однородную систему линейных уравнений Ах = 0, что множество координатных столбцов всех векторов из L в базисе е будет совпадать с множеством всех решений системы Ах = 0.

Применяя формулу х’_а = Т

1 х_е преобразования координат (см. формулу (4.24) в п. 4.6), которая в подробной записи имеет вид

Однородную систему линейных уравнений, описывающую данное линейное подпространство L, называют общими уравнениями этого подпространства. Общие уравнения подпространства определяются неоднозначно: достаточно систему линейных уравнений, описывающую подпространство, заменить любой эквивалентной системой, чтобы получить другие общие уравнения того же подпространства. Вид общих уравнений подпространства, получаемых с помощью процедуры, указанной в доказательстве теоремы 4.22, зависит от выбора базиса в L и выбора векторов, дополняющих этот базис до базиса в пространстве X.

обратной к которой является матрица

В силу теоремы 4.21, линейное подпространство в базисе а описывается однородной системой уравнений

Применив формулу преобразования координат х’_а = Т 1 х_е, которая в данном случае в подробной записи имеет вид

систему х‘₃ = 0, х‘₄ = 0 преобразуем в систему описывающую линейное подпространство L в базисе е.

Если подпространство задано общими уравнениями, то для построения базиса этого подпространства следует построить фундаментальную систему решений для общих уравнений подпространства.

При мер 4.19. Найти какой-либо базис подпространства L, заданного системой уравнений

Решение. Выбрав в качестве главных неизвестные х, Х2, а свободных — хз, Х4, решим систему. В результате получим общее решение

которое называют параметрическим уравнением подпространства L в векторной форме.

Решение. Векторное уравнение (4.37) в данном случае имеет

Переходя к координатам, получаем координатную форму параметрических уравнений

Пусть в линейном пространстве X даны подпространства L и L2. Множество Ь П L2 векторов, принадлежащих как Ь, так и L2, является подпространством в X. Его называют пересечением подпространств Li И 1/2-

L1+L2. Если при этом пересечение ЬГЬ2 — нулевое подпространство, то сумму L + L2 называют прямой суммой и обозначают через L ® Z/2-

Аналогично для любого числа а имеем: ах = аа + ab € L + L2, так как аа € Li и аб € L2.

Понятия пересечения и суммы подпространств распространяются на любое число подпространств.

Решение. Векторы ai и аг линейно независимы и поэтому составляют базис в подпространстве Ь. Дополним систему векторов а, т и 62 = (0,0,0,1) т и положим L2 = (61,62)- Очевидно, что L/2 является искомым подпространством. Далее запишем векторное равенство

перейдем от него к покоординатным уравнениям (см. разд. 4.2) и, решив систему этих уравнений, найдем: оц = «2 = 1, fi = 3, Р2 = 5. Поэтому

столбцов этих векторов и в этой матрице выделить какой-либо базисный минор. Векторы, на координатных столбцах которых находится базисный минор, образуют базис в подпространстве L1+L2. Отметим, что базисный минор можно выбирать не в исходной, а в преобразованной матрице (после выполнения последовательности элементарных преобразований строк).

Решение. Составим матрицу

Проводя элементарные преобразования строк матрицы, приведем ее к ступенчатому виду:

Если пространства L и L₂ заданы однородными системами уравнений, то пересечение Ь П L₂ будет определяться системой, получаемой объединением всех уравнений двух систем. Любая фундаментальная система решений такой системы уравнений дает базис пересечения L Г)Ь₂.

Пример 4.23. Найти базис пересечения подпространства Ь, заданного системой уравнений

и подпространства L2, заданного системой уравнений

Решение. Составим объединенную систему уравнений

и найдем ее общее решение

Они и представляют собой один из базисов подпространства Ь П L2.

Если подпространства L и L2 заданы как линейные оболочки систем векторов

то при построении базиса пересечения L П L2 этих подпространств достаточно перейти к описанию этих подпространств общими уравнениями, а затем действовать, как в последнем примере: объединяя две однородные системы в одну, искать фундаментальную систему решений объединенной системы.

Существуют и другие способы построения базиса пересечения. Например (см. [21], решение задачи 1319), можно составить векторное уравнение

с неизвестными ai, од, . од, Pi, P2, • ••, Pi и от него перейти к системе покоординатных уравнений. Это линейная однородная система. Построив фундаментальную систему решений этой системы, для каждого решения из ФСР вычислим, например, левую часть векторного уравнения (4.39). Получим систему векторов, порождающую линейное пространство L П L2. Теперь базис в L П L2 можно построить, выделив в этой системе векторов максимальную линейно независимую подсистему. Отметим, что если система векторов 01, Пример 4.24. Найти базис пересечения подпространств Ь =

Решение. Сначала используем первый способ, переходя к общим уравнениям подпространств. Подпространство L описывается параметрическим уравнением х = t а + t2 0,2 + Сз «з, которое в координатной форме имеет вид:

Теперь применим второй способ решения примера. Составим векторное уравнение

в подробной записи имеющее вид:

Переходя к покоординатным уравнениям, получим однородную систему

с шестью неизвестными. Ее общее решение таково:

Свободных неизвестных два, и фундаментальная система решений состоит из двух столбцов

В этих двух столбцах выбираем первые три компоненты и принимаем их в качестве значений 04, o₂, ад в выражении ац а + а₂ + од «3. Получаем два вектора

Теорема 4-23. В конечномерном линейном пространстве X размерность суммы L + L₂ подпространств Li w L₂ равна сумме размерностей этих подпространств минус размерность их пересечения, т.е.

и докажем, что она является базисом в L + L2.

Система векторов (е, f,g) линейно независима. Чтобы доказать это, запишем равенство

и покажем, что оно возможно только при нулевых значениях всех коэффициентов. В равенстве (4.41) объединим слагаемые, относящиеся к векторам систем ей/:

Вектор а принадлежит подпространству L. Но из равенства (4.41) следует, что

Поскольку система векторов (е,д) линейно независима (как базис в Z/2), это равенство возможно лишь при нулевых значениях всех коэффициентов:

Таким образом, доказано, что равенство (4.41) выполняется лишь при нулевых значениях всех коэффициентов, а система (е, /, д) линейно независима и является базисом в подпространстве Ь + L2. Число векторов в этом базисе, а потому и размерность пространства L + L2, равна к + I + т. Поскольку cliniLi — к + I, dim L2 = к + т, dim(Li П L2) = к, то

Источник