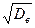Найти методом моментов по выборке точечную оценку параметра

Приняв во внимание, что математическое ожидание показательного распределения равно 1 /X (см. гл. 13, § 3), имеем

Отсюда

Итак, искомая точечная оценка параметра X показательного распределения равна величине, обратной выборочной средней:

Б. Оценка двух параметров. Пусть задан вид плотности распределения f(x; 0_Г 0₂), определяемой неизвестными параметрами 0, и 0₂. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:

Математическое ожидание и дисперсия есть функции от 0, и 0₂, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными 0! и 0₂. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки 0* и 02- Эти оценки являются функциями от вариант выборки:

Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка:

Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна а 2 (см. гл. 12, § 2), имеем:

Итак, искомые точечные оценки параметров нормального распределения:

Замечание 1. Для оценок неизвестных параметров можно приравнивать не только сами моменты, но и функции от моментов. В частности, этим путем получают состоятельные оценки характеристик распределений, которые являются функциями теоретических моментов. Например, асимметрия теоретического распределения (см. гл. 12, § 9)

есть функция от центральных моментов второго и третьего порядков. Заменив эти теоретические моменты соответствующими эмпирическими моментами, получим точечную оценку асимметрии

Замечание 2. Учитывая, что у[т^ = yjl = а_в, последнюю формулу можно записать в виде

Далее эта оценка будет принята в качестве определения асимметрии эмпирического распределения (см. гл. 17, § 9).

Источник

Метод моментов

Содержание:

Метод моментов, предложенный английским статистиком Карлом Пирсоном в 1894 г., заключается в приравнивании определенного числа выборочных моментов к соответствующим теоретическим, которые являются функциями неизвестных параметров Рассматривая количество моментов, равное числу к неизвестных параметров, подлежащих определению, и решая полученные уравнения относительно этих параметров, получаем искомые оценки. Иначе говоря, оценки параметров являются решениями систем уравнений или , для некоторых

Метод моментов содержит неопределенность, поскольку можно получить уравнения для неизвестных параметров , используя как начальные, так и центральные моменты, а также некоторые их модификации типа асимметрии или эксцесса.

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Пример:

Функция

задает плотность распределения Рэлея (см. § 6.4). Требуется оценить параметр по выборке

Найдем оценку параметра 0, приравнивая начальные выборочные и теоретические моменты. Первый начальный момент

имеет вид: Приравнивая, получаем первую оценку параметра:

Приравнивая вторые начальные моменты, можем получить другую оценку: из уравнения, которое получитсяся при использовании второго центрального момента (дисперсии), — третью оценку:

В общем случае система уравнений для моментов может не иметь решения в элементарных функциях (и тогда можно искать решение приближенными методами) или вообще оказаться неразрешимой (несовместной).

Оценки, полученные методом моментов, часто оказываются смешенными. К достоинствам метода моментов следует отнести его простую вычислительную реализацию, а также то, что оценки являются функциями от выборочных моментов.

В силу теоремы Слуцкого любая непрерывная функция от выборочных моментов функции сходится по вероятности к постоянной, получаемой подстановкой в эту функцию теоретических моментов, если они существуют и если получаемая таким образом постоянная конечна. Для определенности рассмотрим функцию от двух моментов (начальных или центральных), хотя ее можно обобщить на любое конечное число аргументов, в том числе и на случай, когда Н зависит только от одного аргумента.

Теорема 1. (Крамера). Пусть в некоторой окрестности точки функция непрерывна и имеет непрерывные частные производные первого и второго порядка:

Тогда для любой выборки, по которой найдены оценки , случайная величина асимптотически нормальна при следующими параметрами:

Иногда оценки, получаемые с помощью метода моментов, принимаются в качестве первого приближения, по которому можно построить другими методами оценки более высокого качества.

Оценки метода моментов используются также, когда существует необходимость оценить не сами параметры распределения (которые часто представляют собой некие абстракции), а определенные практически значимые показатели, зависящие от этих параметров функционально: . Самый простой (хотя и не самый точный) способ такого оценивания — подставить полученные оценки в соответствующую функцию:

Если распределение определяется одним параметром, то для построения оценки один теоретический момент приравнивают к одному эмпирическому моменту того же порядка (обычно первого).

Возможно вам будут полезны данные страницы:

Источник

Метод моментов для точечной оценки параметров распределения

А. Оценка одного параметра. Пусть задан вид плотности распределения f(x,θ), определяемой одним неизвестным параметром θ. Требуется найти точечную оценку параметра θ.

Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν₁ = М₁. Учитывая, что ν₁ = М(X) (см. гл. VIII, § 10), М₁ = (см. гл. XVII, § 2), получим

М(X)= (*)

Математическое ожидание М(X), как видно из соотношения

,

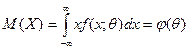
есть функция от θ, поэтому (*) можно рассматривать как уравнение с одним неизвестным θ. Решив это уравнение относительно параметра θ, тем самым найдем его точечную оценку θ*, которая является функцией от выборочной средней, следовательно, и от вариант выборки:

θ*=

М(X)=

Приняв во внимание, что математическое ожидание показательного распределения равно 1/λ (см. гл. XIII, § 3), имеем

1/λ= .

λ=1/ .

Итак, искомая точечная оценка параметра λпоказательного распределения равна величине, обратной выборочной средней:

λ*=1/ .

Б. Оценка двух параметров.Пусть задан вид плотности распределения f (х; θ₁, θ₂), определяемой неизвестными параметрами θ₁ и θ₂. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:

Учитывая, что что ν₁ = М(X), μ₂ = D(Х)(см. гл. VIII, § 10), М₁ = , m₂ = D_в (см. гл. XVII, § 2), получим

(**)

Математическое ожидание и дисперсия есть функции от θ₁ и θ₂, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными θ₁ и θ₂. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки θ₁* и θ₂*. Эти оценки являются функциями от вариант выборки:

Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка:

Учитывая, что ν₁ = М(X), μ₂ = D(Х), М₁ = , m₂ = D_в, получим

.

Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна σ 2 (см. гл. XII, § 2),имеем:

а = , σ 2 = D_в.

Итак, искомые точечные оценки параметров нормального распределения:

а* = , σ*=

Замечание 1. Для оценок, неизвестных параметров можно приравнивать не только сами моменты, но и функции от моментов. В частности, этим путем получают состоятельные оценки характеристик распределений, которые являются функциями теоретических моментов. Например, асимметрия теоретического распределения (см. гл. XII, § 9)

есть функция от центральных моментов второго и третьего порядков. Заменив эти теоретические моменты соответствующими эмпирическими моментами, получим точечную оценку асимметрии

.

Замечание 2. Учитывая, что , последнюю формулу можно записать в виде

Далее эта оценка будет принята в качестве определения асимметрии эмпирического распределения (см. гл. XVII, § 9).

Источник

Математическая статистика

Точечные оценки

Методы получения точечных оценок

Точечной оценкой неизвестного параметра θ, вообще говоря, может являться любая статистика. Однако на практике интерес представляют лишь наиболее «качественные» оценки, для которых вероятность того, что при реализации случайной выборки они примут значение максимально близкое к неизвестному значению θ наибольшая. Такие оценки должны быть несмещёнными, состоятельными и эффективными. Возникает вопрос, как получить качественную оценку для произвольного параметра θ наблюдаемой случайной величины X?

1. Метод подстановки

Например, согласно методу подстановки оценкой математического ожидания будет выборочное среднее, а оценкой дисперсии – выборочная дисперсия.

Все оценки, рассчитанные по методу подстановки, являются состоятельными, однако их несмещённость и эффективность не гарантированы. Примером смещённой оценки, рассмотренной ранее, является выборочная дисперсия.

Метод моментов состоит нахождении такого вектора параметров θ, при котором теоретические моменты равны выборочным моментам, т.е. в разрешении системы уравнений вида:

Число уравнений в системе (1) равно числу неизвестных параметров k. Для получения оценок по методу моментов, вообще говоря, могут быть выбраны любые моменты произвольных порядков, однако, как правило, на практике используют лишь моменты низших порядков.

Все оценки, рассчитанные по методу моментов, являются состоятельными, однако их несмещённость и эффективность, так же, как и в случае метода подстановки, не гарантированы.

Точечные оценки, полученные по методу моментов, называются ММ-оценками.

Пример 1

3. Метод максимального правдоподобия

Метод максимального правдоподобия (maximum likelihood estimation, MLE) является наиболее популярным методом оценивания неизвестных параметров распределений.

Учитывая, что компоненты X₁,…, X_n случайной выборки, реализациями которых являются выборочные значения x ₁,…,x_n, независимы, многомерная функция плотности есть произведение одномерных функций плотностей:

В (2) учтено, что все компоненты X₁,…, X_n имеют одинаковое распределение, совпадающее с распределением генеральной совокупности X.

Функция правдоподобия выборки x₁,…, x_n является функцией только вектора неизвестных параметров θ.

Запишем необходимое условие экстремума функции правдоподобия:

На практике бывает удобно вместо системы уравнений (3) составить систему уравнений

Все оценки, рассчитанные по методу максимального правдоподобия, являются состоятельными и, по крайней мере, асимптотически несмещёнными и асимптотически эффективными. Если для неизвестного параметра существует эффективная оценка, то метод максимального правдоподобия даёт именно эту оценку.

Точечные оценки, полученные по методу максимального правдоподобия, называются МП-оценками.

Источник

Метод моментов для точечной оценки параметров распределения

Пусть известен вид функции плотности распределения вероятностей случайной величины, зависящей от одного неизвестного параметра 0.

Xx — показательное распределение (,х > 0). Требуется найти точечную оценку параметра 0. Для показательного распределения 0 = X •

Для получения оценки одного параметра можно использовать одно уравнение с одним неизвестным. В методе моментов в качестве такого уравнения предлагается равенство начального теоретического момента первого порядка и начального эмпирического момента первого порядка

где v, — начальный теоретический момент первого порядка, М_х — эмпирический момент первого порядка.

Теоретический момент первого порядка, как известно, представляет собой математическое ожидание, а эмпирический момент первого порядка — это выборочная средняя. Таким образом, имеем

Математическое ожидание можно рассматривать как функцию параметра 0:

Учитывая то, что из уравнения (9.13)_можно получить не сам параметр 0, а только его оценку, так как х_в является реализацией случайной величины Х_в, получаем равенство

Решив это уравнение, находим оценку 0*, которая является функцией от выборочной средней. Так, для экспоненциального распределения имеем

В том случае, когда плотность распределения вероятностей зависит от двух параметров, 0 следует рассматривать как двумерный вектор. Но тогда для оценки этих параметров требуется составлять не одно, а два уравнения. Такими уравнениями могут быть равенства

Источник