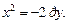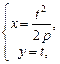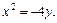Найти параметр параболы как найти

Параметры параболы

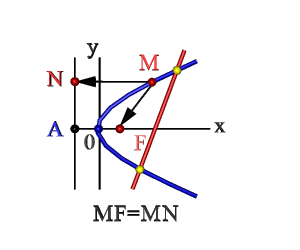
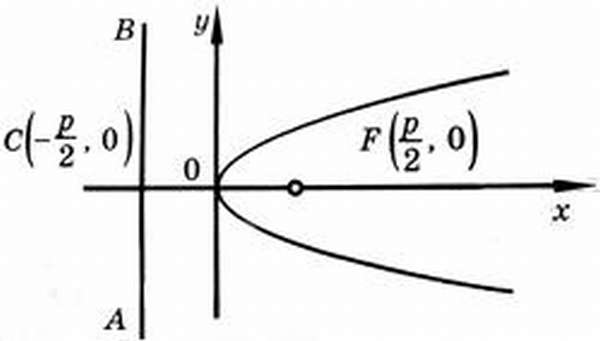
Точка F(p/2, 0) называется фокусомпараболы, величина p – параметром, точка О(0, 0) – вершиной (рис. 9.15). При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

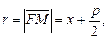
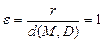
Величина где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина называется эксцентриситетомпараболы.

Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 9.15).

Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 9.16):

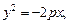
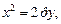
а) б) в)

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:

где t – произвольное действительное число.

Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:

1) 2)

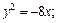
Решение.1) Уравнение y 2 = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y 2 = –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 9.17).

2) Уравнение x 2 = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x 2 = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 9.18).

Пример 2.Определить параметры и вид кривой x 2 + 8x – 16y – 32 = 0. Сделать рисунок.

Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:

(x + 4) 2 – 16 – 16y – 32 = 0;

В результате получим:

Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх 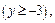осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).

Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = –3 и точки F(0; 3).

Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x 2 = 2py с параметром p = 2 × 3 = 6, т. е. x 2 = 12y (рис. 9.20).

Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).

Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Следовательно, искомое уравнение

Дата добавления: 2015-09-29 ; просмотров: 6956 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Парабола: формулы, примеры решения задач

Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы имеет вид:

,

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.

В математическом анализе принята другая запись уравнения параболы:

Фокус параболы имеет координаты

Директриса параболы определяется уравнением .

Расстояние r от любой точки параболы до фокуса определяется формулой .

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.

Пример 1. Определить координаты фокуса параболы

Находим координаты фокуса параболы:

Пример 2. Составить уравнение директрисы параболы

Получаем уравнение директрисы параболы:

Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.

Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.

Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.

Источник

Квадратичная функция. Построение Параболы

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

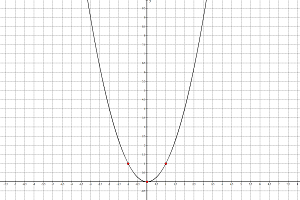
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Рассмотрим три случая:

Если a > 0, то график выглядит как-то так:

0″ height=”671″ src=”https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=”602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Как строим:

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Как строим:

Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)

Как строим:

Источник

Алгоритм нахождения коэффициентов а, в и с по графику квадратичной функции

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

Описание презентации по отдельным слайдам:

Алгоритм нахождения значения коэффициентов a, b, c по графику квадратичной функции y= ax2 +bx+c. Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Нахождение коэффициента a 1) по графику параболы определяем координаты вершины (m,n) 2) по графику параболы определяем координаты любой точки А (х1;у1) 3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде: 4) решаем полученное уравнение.

По графику функции найдите значения коэффициентов a, b, c

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Номер материала: ДВ-373901

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Число бюджетных мест на IT-направлении к 2024 году увеличат вдвое

Время чтения: 2 минуты

В украинском университете открылся первый в мире факультет TikTok

Время чтения: 1 минута

Всероссийская олимпиада школьников начнется 13 сентября

Время чтения: 2 минуты

ЕГЭ в 2022 году может пройти в допандемийном формате

Время чтения: 1 минута

Студентов МГУ обязали проходить курс по искусственному интеллекту

Время чтения: 1 минута

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Парабола свойства и график квадратичной функции

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x2 + b x + c (узнаваемый шаблон: y = x2).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

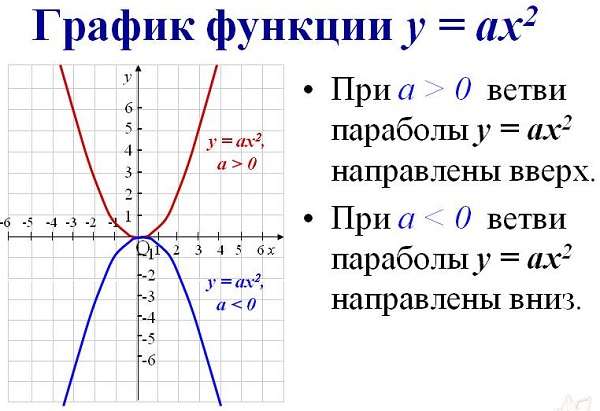
Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

Пример.

Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.

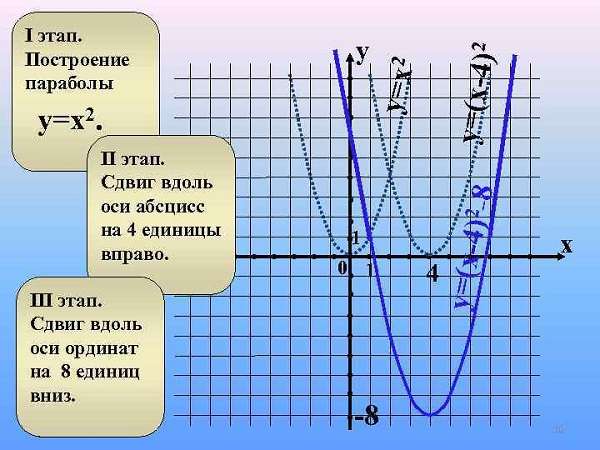
Смещение параболы

Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

Анализируя выражения и уравнения, можно увидеть следующее:

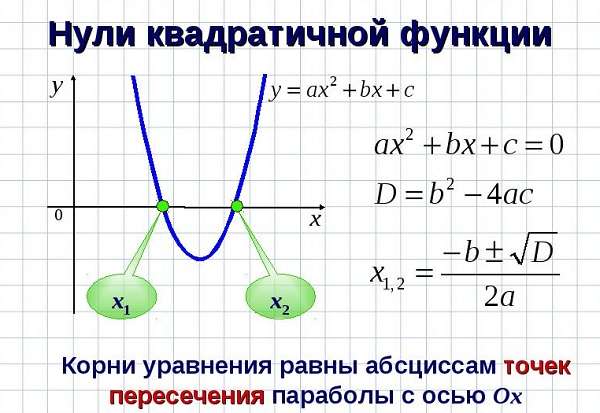
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

Получаем алгоритм построения параболы:

Пример 1.

Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

Источник