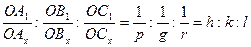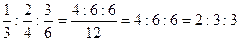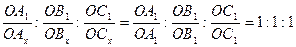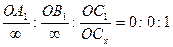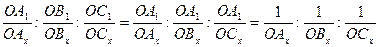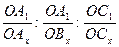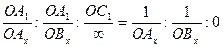Найти параметры вейса для плоскости 212

Установка кристаллов

Для определения кристаллографических символов и изображения стереографических проекций пользуются стандартными международными правилами установки кристаллов.

Установка кристалла – это выбор кристаллографических осей, единичной (масштабной) грани и его ориентировка в пространстве относительно этих осей и грани.

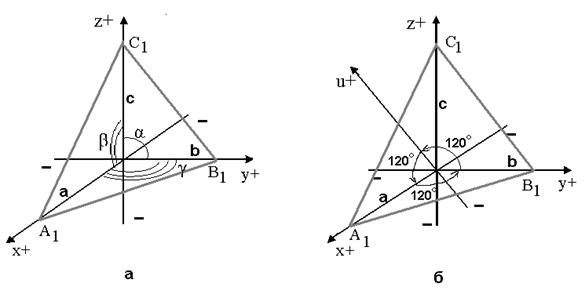
Кристаллографические системы координат зависят от симметрии кристаллов и изменяются по сингониям. Для кристаллов тригональной и гексагональной сингоний принимаются четыре оси x, y, z, u, а для остальных сингоний x, y, z.

В кристаллографии используется два вида кристаллографических осей: трехкоординатная и четырехкоординатная система (рис. 5.2). Четырехкоординатная система используется в тригональной и гексагональной сингониях, а трехкоординатная – для кристаллов триклинной, моноклинной, ромбической, тетрагональной и кубической сингоний.

Единичную грань принимают таким образом, чтобы она пересекала либо все координатные оси, либо максимальное их число. При этом масштабные отрезки, отсекаемые ею, принимаются за единицы измерения по соответствующей координатной оси.

Для каждой сингонии характерными являются углы между координатными осями: между x и y –α, между z и x – β, между x и y – γ и масштабные отрезки (единичные параметры) на координатных осях: на оси x отрезок обозначается а, на оси у – в, на оси z – с.

Оси координат располагаются в соответствии с симметрией кристаллов либо по осям симметрии, либо по нормалям к плоскостям, а если их нет – по ребрам кристаллического многогранника. В табл. 5.1 приведены правила установки кристаллов по сингониям, а также характеристики координатных систем. Фактически в каждой сингонии своя система координат, которая отличается от системы координат другой сингонии координатными углами и единичными параметрами. Только в тригональной и гексагональной сингониях используется единая четырехкоординатная система.

5.3 Закон Гаюи

Открыл этот закон в 1784 году Жан Огюст Гаюи. Это учение о символах основывается на одном из важнейших законов кристаллографии – законе рациональности отношений параметров (закон Гаюи).

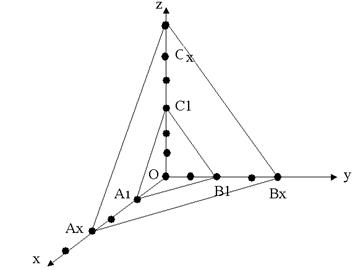
Предположим, что тщательно изучив наши рекомендации по установке кристаллов, вы правильно расположили модель кристалла в координатной системе, приняв за координатные оси три непараллельных ребра. А теперь пронаблюдайте, где пересекают координатные оси две грани Вашего кристалла при их мысленном продолжении (рис. 5.3). Одна – единичная, А₁,В₁,С₁, выбранная в соответствии с сингонией по правилам табл. 5.1, отсекает отрезки ОА₁, ОВ₁, ОС₁, называемые единичными параметрами. Другая непараллельная грань (A_x, B_x, C_x) характеризуется параметрами ОA_x, ОB_x, ОC_x.

Закон Гаюи гласит: двойные отношения параметров, отсекаемые двумя любыми гранями кристалла на трех пересекающихся ребрах его, равны отношениям целых и сравнительно малых чисел

(параметры Вейса)

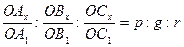
Наличие малых чисел связано с тем, что реальные грани кристаллов построены не любыми плоскими сетками, а только теми, которые обладают наибольшей плотностью расположения в них элементарных частиц.

Закон Гаюи связывает внешнюю форму кристаллов с их внутренним решетчатым строением.

При практическом применении закона Гаюи для определения индексов граней пользуются обратными отношениями параметров, получивших название индексов Миллера:

Индексы Миллера – это величины, обратные параметрам Вейса, приведенные к целым числам. Для получения индексов Миллера в виде трех взаимно простых чисел проводят следующие математические преобразования:

— приводят дроби к общему знаменателю,

— находят дополнительный множитель,

— отбрасывают общий знаменатель,

— сокращают полученное соотношение на общий множитель.

Для примера определим индексы Миллера грани А_xВ_xС_x (рис. 5.3), параметры выразим числом промежутков между элементарными частицами (или в мм, см):

Условное обозначение символов:

Если грань пересекает какую-то ось с отрицательной стороны, то над индексом по этой оси ставят знак минус ( ).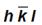

В качестве символа простой формы выбирается грань, обладающая максимальным количеством положительных индексов.

На практических занятиях по кристаллографии отрезки, отсекаемые гранями на координатных осях определяем приблизительно при помощи линейки и карандаша. Более точные вычисления производятся на основании специальных формул с применением гониометрических измерений.

5.4 Практические рекомендации по определению кристаллографических символов

Практические рекомендации по определению кристаллографических символов заключаются в следующем:

2. Если грань, в том числе единичная, параллельна одной или двум координатным осям, то индекс, соответствующий данным осям, равен нулю. Пусть грань параллельна оси x и y, т. е.

3. Для определения символа грани кристалла кубической сингонии достаточно измерить ее отрезки, которые отсекает эта грань по координатным осям, и взять величины им обратные, т.к. ОА₁=ОВ₁= ОС₁.Тогда

Индексы некоторых простых форм кубической сингонии:

гексаэдр<100>, октаэдр<111>, тетраэдр<111>, ромбододекаэдр <110>, пентагондодекаэдр , тетрагексаэдр , гексаоктаэдр

4. В тетрагональной сингонии ОА₁= ОВ₁≠ ОС₁, поэтому общая формула 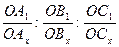принимает вид

В случае вертикальных граней, т.е. при ОС_x= ∞

Индексы некоторых простых форм тетрагональной сингонии:

пинакоид <001>, моноэдр <001><001>, тетрагональные призмы <100>,<110>,, тетрагональные пирамиды и дипирамиды <111>, <101>, , , .

5. В триклинной, моноклинной и ромбической сингониях часто реальная единичная грань, пресекающая все три координатные оси, отсутствует. В указанных сингониях чаще всего используются индексы .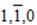

Индексы некоторых простых форм низшей категории:

Ромбические призмы и диэдры <110>, <101>, <011>, , <0kl>, ромбические пирамиды и дипирамиды <111>, .

Возможны два случая установки:

1) Грань, отсекающая равные отрезки на двух соседних осях, образующих друг с другом угол 60°, проходит параллельно третьей (рис.5.5а).

Рисунок 5.5 – Варианты установки кристаллов тригональных и гексагональных сингоний

2) Грань, отсекающая равные отрезки на двух горизонтальных осях, образующих угол 120° и пересекает третью ось (рис. 5.5б). Отрезок по последней оси вдвое короче отрезков по двум другим осям.

Для примера обозначения граней кристаллов с помощью символов вернемся к рис.5.1. Согласно правилу установки (табл.5.1), ось z выбираем вдоль L₄. оси x, y в случае а) – по осям L₂,проходящим через середины ребер кристалла; в случае б) – по осям L₂, проходящим через середины граней. Тогда единичная грань дипирамиды и в том, и в другом случае отсекает на двух горизонтальных осях равные масштабные отрезки и неравный отрезок по третьей оси.

1.Установка кристалла в случае (а)

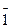
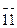
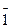
Призма: индексы граней (110), ( 10), ( 0), (1 0); обобщенный символ простой формы<110>.

2. Установка кристалла в случае (б)

Дипирамида: Индексы граней и символ простой формы аналогично (а).

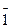
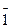
Призма: индексы граней (100), (010), ( 00), (0 0); обобщенный символ простой формы призмы<100>.

Приведенные символы дают ясное представление о неодинаковом расположении граней на обоих кристаллах.

Источник

Параметры Вейсса и индексы Миллера

В кристаллографии принято характеризовать плоскости (или нормали к ним) не параметрами, а так называемыми индексами Миллера. Индексы Миллера — это величины, обратные параметрам Вейсса, приведенные к целым числам. Если параметры плоскости р : q : r, то индексы Миллера определяются из соотношения

(3.1)

В приведенном примере (см. рис. 9) имеем .

Числа h, k, l называются индексами плоскости; индексы, написанные подряд и заключенные в круглые скобки. ‑ (hkl) называют символом плоскости: в нашем примере это (230).

Символом (hкl) характеризуется вся совокупность параллельных плоскостей. Этот символ означает, что система параллельных плоскостей рассекает отрезок а на h частей b на k частей и с на l частей, т. е. отсекает на осях координат отрезки а/h, b/к, c /l. Значит, чтобы построить плоскость (hkl), надо нанести на осях координат эти отрезки и провести через них плоскость. В общем, виде уравнение плоскости (hк1) и всего семейства параллельных ей плоскостей будет

где N ‑ всегда целое число, h, к, l ‑ взаимно простые, целые числа. Для плоскости, проходящей через начало координат. N = 0; для плоскости, ближайшей к началу координат, N = 1.

Запишем уравнение плоскости АВС в параметрической форме: Ах + Ву + Сz = N

Или плоскости проходящей через начало координат Ах + Ву + Сz = 0, здесь х, у, z ‑ текущие координаты, которые можно выразить через параметры кристалла а, b, с как х =ma, у = nb, z=pc, где m, п, р ‑ целые числа.

Подставим в это уравнение координаты двух любых точек, лежащих в плоскости:

и возьмем отношение

Определители, составленные из целых чисел, должны быть целыми числами, значит Aa=hN, Bb=kN, Cc=lN, где h, k, l ‑ целые, взаимно простые числа, N ‑ общий множитель. Величины h, k, l обратно пропорциональны длинам отрезков, отсекаемых этой плоскостью на осях координат. Таким образом, в общем виде, уравнение плоскости можно записать как формулу (2).

1. Найти символ плоскости. Отсекающей на осях координат отрезки 4а, 3b, 2с.

Значит, символ плоскости (hkl) = (346).

2. Найти символ плоскости, параллельной осям X и Z и отсекающей три единицы на оси Y.

Имеем отсюда

3. Определить символ направления, проходящего через начало координат O и точку с координатами (a/8, 3b/8, 5c/8)

Найдем целочисленные значения отношений координат:

Это соответствует переносу заданной точки вдоль заданного направление в ближайший началу координат узел кристаллической решетки с координатами (1, 3, 5). Значит, символ заданного направления [135].

4. Определить символ направлении, проходящего через точки А (0, b/2, с/2) и В (a/2, 0. с/2).

Вычитая соответственно координаты одной точки из координат другой, что соответствует параллельному переносу вектора АВ в начало координат О. получаем новые координаты конца вектора (-а/2, b/2, 0). Таким образом, решение этой задачи сведено к предыдущей; заменим полученное Отношение целочисленным

Символ заданного направления [110].

Из последнего примера видно, что если плоскость параллельна оси координат, т. е. пересекается с этой осью в бесконечности, то индекс плоскости по этой оси будет 1/ = 0 (рис. 10).

Символы координатных плоскостей независимо от углов между осями всегда будут:

Рис. 10. Символы некоторых плоскостей в кубической ячейке

Источник

5.2.1.3 Векторы и плоскости решетки. Индексы Вейса и Миллера.

Из ВЕКТОРОВ ЭЛЕМЕНТАРНЫХ ТРАНСЛЯЦИЙ можно составить произ-

где n,m,l – целые числа. Такие (и только такие) векторы мы будем назы-

вать ВЕКТОРАМИ ТРАНСЛЯЦИИ РЕШЕТКИ или просто ВЕКТОРАМИ РЕШЕТ-

Очевидно, что, сместив любой узел на вектор решетки (5.2.1), мы попадем в такой же узел. Кроме того, подобрав соответствующий вектор из набора (5.2.1), мы можем сместиться из любого узла в любой другой. Эта периодическая воспроизводимость структуры при смещении в

Наконец, третий существенный момент: смещение всей решетки как целого на любой вектор (5.2.1) ничего не изменит. Решетка бесконечна, все узлы идентичны и все они в смещенной решетке точно совпадут с узлами исходной. Важно бывает лишь обозначить направление смещения, если мы рассматриваем ориентацию кристалла или направление движения частицы в нем. Поэтому не имеет смысла различать кратные векторы.

именно к вектору решетки. Запятые между индексами не ставятся, так что используемые индексы Вейса имеют вид: [ nml ].

шими соседями. Поэтому основными осями (или просто осями кристалла ) называют именно оси с минимальными индексами.

Вследствие наличия трансляционной симметрии в кристалле имеется бесконечное множество одинаковых векторов или параллельных осей. Поэтому в двух непараллельных направлениях всегда можно выбрать пары пересекающихся осей. Построенные на них плоскости (также бесконечное множество, причем все параллельны либо совпадают)

будем называть КРИСТАЛЛОГРАФИЧЕСКИМИ ПЛОСКОСТЯМИ.

a 1 a 2

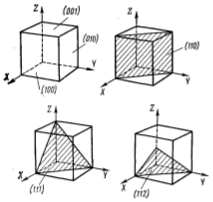
Рис. 5.2.5. Некоторые из основных плоскостей кубического кристалла и их индексы Миллера.

Если плоскость параллельна какой-либо оси (т.е. «пересекает ее на бесконечности»), то соответствующий индекс равен нулю.

В тех случаях, когда плоскость пересекает отрицательную полуось, знак «-» ставят над соответствующим индексом, см. рис. 5.2.5.

5.2.1.4 Сингонии, решетки Браве, кристаллографические классы

ГРАФИЧЕСКИХ ГРУПП (группы Федорова). Поясним, что это такое.

При некоторых соотношениях между длинами ЭЛЕМЕНТАРНЫХ ВЕК-

ТОРОВ ТРАНСЛЯЦИИ и углов между ними в ПРИМИТИВНОЙ РЕШЕТКЕ мо-

гут возникать дополнительные элементы симметрии, в первую очередь

– оси вращения, плоскости отражения и их комбинации. Например, в

Таблица 5.2.1. Кристаллографические сингонии.

Источник

5.4. Индексы граней Вейса и Миллера.

Индексы Миллера, заключенные в круглые скобки, называются символом грани (hkl). Знаки отношений в этой записи опускаются, но подразумеваются. Если какой-либо из индексов отрицателен (грань пересекает ось координат с отрицательного конца), то знак минус ставится над индексом: (hk̅l), и это читается не «минус k», а «k с минусом».

5.5. Морфологическое индицирование граней. Закон Аюи.

Чтобы использовать закон Аю и для морфологического индицирования граней кристалла, выберем параметры одной из граней, показанных на рис. 5.9, за единицы измерения по координатным осям: A₁=a, B₁=b, C₁=c. Тогда, в соответствии с результатами предыдущего раздела, имеем a/A₂ :b/B₂ : c/C₂ = h₂: k₂: l₂, т.е. получаем индексы Миллера второй грани рисунка 5.9. Далее, используя эти же масштабы, можем проиндицировать и все остальные грани данного кристалла. Грань, выбранная нами за масштабную, называется единичной гранью, поскольку она задает единицы измерения по координатным осям, и поскольку ее символ (111) содержит только единицы. Обращаем внимание, что в частных случаях некоторые из индексов могут быть отрицательными, например, (11̅1) – это не влияет на «единичность» грани.

Источник

Кристаллическая решётка. Элементарная ячейка

Структура кристалла– это конкретное расположение частиц в пространстве (физическая реальность). Чтобы представить структуру кристалла, нужно знать относительные размеры частиц, расстояния между ними, силы связи ме­жду частицами, их взаимное расположение, повторяющее расположение частиц в пространстве (пространственную решётку), и законы симметрических преоб­разований.

Симметрия– основная особенность, характерная для структуры кристаллов. Теорию строения структуры кристаллов развил английский учёный Бравэ, основываясь на многих экспериментальных результатах других исследовате­лей. Положив в основу своей теории анизотропию и симметрию кристаллов, он пришёл к понятию о пространственной решётке.

Рис. 1.11.Пространственные решётки некоторых веществ

Рассмотрим простейший случай, когда одинаковые частицы расположены в кристалле параллельными бесконечными рядами. На 1 мм в кристалле находится порядка 10 7 частиц (рис. 1.12). Трансляция(период идентичности) –симметричное преобразование, при котором точка (частица) повторяется в пространстве. Её величина – кратчайшее из возможных расстояний между одина­ковыми точками в ряду.

Рис. 1.12.Линейная цепочка атомов

Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то ряд совместится сам с собой, его вид не на­рушится. Выбор основных трансляций в структуре кристалла очень важен, по­тому что ими определяются кристаллографические системы координат. В об­щем случае это косоугольные координаты с разными масштабными отрезками по осям (рис. 1.13).

Узлы ряда– одинаковые точки, связанные между собой величиной трансляции ав бесконечном ряду. При перенесении точек по трём направлениям на величину трансляций а, b, c можнополучить трёхмерную сетку.

Ячейки сетки– параллелограммы, вершины которых являются узлами.

Элементарная ячейка– параллелепипед с характерным для данной решётки расположением частиц, с помощью которого весь кристалл может быть построен путём его многократного повторения в трёх направлениях. Она стро­ится на трёх элементарных трансляциях а, b, с. Элементарную ячейку принято выбирать так, чтобы она удовлетворяла следующим условиям: наилучшим об­разом отражала симметрию сетки, имела бы прямые углы и, если возможно, обладала бы наименьшим объёмом.

Примитивнойназывается элементарная ячейка, внутри которой нет узлов, частицы содержатся только в вершинах (рис. 1.13). Узлы решётки– вершины ячеек, в которых располагаются одинаковые атомы или группы атомов. Они эк­вивалентны друг другу.

Период (постоянная) кристаллической ячейки– расстояние между однородными атомами. Параметры элементарной ячейки: три ребра ячейки a, b, c; три угла между ними α, β, γ. Например, для представленной на рис. 1.13 примитивной ячейки, соотношения между параметрами следующие:

Рис. 1.13.Примитивная элементарная ячейка

Элементарные ячейки, составляющие кристаллическую решётку кристалла, имеют одинаковые форму и объём. Кристалл можно построить с помощью разных примитивных ячеек. В некоторых случаях удобно характеризовать про­странственную сетку не примитивной, а сложной элементарной ячейкой, у ко­торой узлы есть не только в вершинах, но и внутри ячейки. Элементарная ячей­ка может содержать несколько примитивных ячеек.

Элементарные ячейкиразличаются по элементам симметрии и степени заполнения атомами (рис. 1.14).

Рис. 1.14.Разные примитивные ячейки в плоской сетке

К элементам симметрииотносятся: трансляции, плоскости симметрии, зеркальные плоскости, оси симметрии разных порядков, инверсионные оси симметрии (рис. 1.15).

Рис. 1.15. Элементы симметрии в кубическом кристалле

Кристаллические ячейки делятся по элементам симмет­рии на 7 сингоний:триклинная, моноклинная, ромбическая, ромбоэдрическая, гексагональная, тетрагональная, кубическая. Сингония в дословном переводе – сходноугольность. В сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинаковая система координат.На рис. 1.16 показана тетрагональная ячейка.

Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии

В каждой сингонии элементарные ячейки делятся по степени заполнения их атомами. Так на одну ячейку простой кубической ячейки имеет приходится 1 атом: n = (1/8)8 = 1; объёмноцентрированной кубической ячейки (ОЦК) – 2 атома: n = (1/8)8 + 1 = 2; гранецентрированной кубической ячейки (ГЦК) – 4 атома: n =(1/8)8 + (1/2)6 = 4 Рис. 1.17); гексагональной с плотной упаковкой (ГПУ) – 2 атома.

Рис. 1.17. Кристаллические ячейки

Кристаллическую решетку общего типа называют решеткой с базисом(БЦК). Решетка с базисом представляется в виде двух вставленных одна в другую подрешеток Бравэ, каждая из которых определяется трансляцион­ными векторами. Базисный вектор устанавливает смещение реше­ток друг относительно друга. Количество базисных векторов может быть сколь угодно большим.

Рис. 1.18.Решётки Браве

Все известные в природе кристаллические тела кристаллизуются в 14 ре­шётках Браве(рис. 1.18). Далее они делятся на 32 класса симметрии и 230 пространственных групп.

Некоторым телам свойственна не одна, а две или более кристаллических структур, устойчивых при различных температурах и давлениях. Такое явление называется полиморфизмом.Полиморфные формы (модификациивещества) имеют, например, углерод и олово. Углеродможет существовать в виде алмаза и графита. Алмаз очень прочный и твёрдый, графит – хрупкий. Элементарные ячейки алмаза и графита относятся к различным сингониям (рис. 1.19).

Рис. 1.19.Кристаллические решётки алмаза и графита

Оловоможет существовать в виде двух модификаций – серого и белого. Серое оловопри температурах ниже 13,3 °С. имеет решётку типа алмаза. При температурах выше 13,3 °С серое олово превращается в белое олово – очень хрупкое вещество, которое легко разрушается в порошок. Белое (металличе­ское) оловоимеет тетрагональную объёмноцентрированную решётку.

ИНДЕКСЫ МИЛЛЕРА

Для описания кристаллических многогранников и структур применяется метод индицирования.Через узлы кристаллической решетки можно провести прямые линии и плоскости. Выберем один из узлов решётки за начало координат.

Любой другой узел решётки определяется радиус–вектором:

Индексы узла– три простых числа [[mnp]], взятые в двойные квадратные или фигурные скобки (рис. 1.20). В системе параллельных прямых всегда можно выделить прямую линию (ряд), проходящую через начало координат. Тогда направление прямой линии определится двумя точками: началом координат и любым узлом ряда.

Индексы направления(прямой линии) – три простых числа [mnp], взятые в квадратные скобки. Эти числа характеризуют положение ближайшего узла, лежащего на прямой линии, проходящей через начало координат.

Рис. 1.20.Миллеровские индексы узлов

Проходящая сквозь узлы прямая, а также ребро кристаллического многогранника имеют наклон в выбранной системе координат. В целом плоские сет­ки в пространственной решётке и соответствующие им грани кристаллического многогранника имеют наклон в системе координат.

Пусть некоторая плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc. Отношение чисел m:n:p характеризует наклон плоскости к осям координат. Серию отношений рациональных чисел m:n:p для всех параллельных плоско­стей можно заменить отношением взаимно простых чисел р:q:r. Числа р, q, r называются параметрами Вейса.

Миллеровские индексы плоскости– три простых числа (HKL), записанные в круглых скобках. Индексы плоскости – дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых лю­бой плоскостью данного семейства на координатных осях Х, У, Z.

Миллеровские индексы опреде­ляются из соотношения чисел р:q:r.

Пусть некоторая плоскость отсекает на осях координат отрезки:

р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:

Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.

Миллеровские индексы данной плоскости (623).

Рис.1.21. Индексы плоскости(623)

Межплоскостное расстояние– это расстояние между параллельными плоскостями, содержащими одинаковое количество атомов. Чем больше индексы H, K, L, тем меньше расстояние между плоскостями. Для кубического кристалла межплоскостное расстояние d для параллельных плоскостей с одинаковыми индексами выражаются через индексы этих плоскостей соотношением:

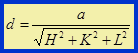
а– постоянная решётки.

В 1819 г. Гаюи сформулировал законцелых чисел(теперь закон Гаюи): для любых двух граней реального кристалла двойные отношения параметров равны отношению малых чисел. На кристаллографическом многограннике образуются лишь такие грани, для которых двойные отношения отрезков, отсекаемых данной гранью и еди­ничной гранью на трёх рёбрах кристалла, принятых за оси координат, равны отношению целых небольших простых чисел.

Грани, для которых отношение р:q:r является иррациональным, в реальном кристалле невозможны. Наклон всякой грани можно определить тремя целыми числами, если за оси координат выбрать направление трёх рёбер кристалла, а за параметры – отрезки, отсекае­мые на этих осях данной гранью.

Источник