Найти параметры вейсса для плоскости 212
3) Метод кристаллографического индицирования. Символы узлов. Символы рядов (ребер).
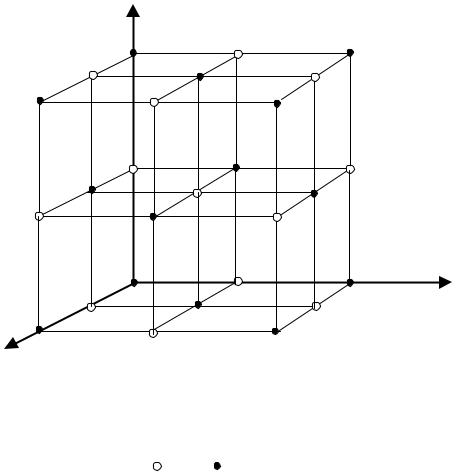
Символы узлов. Если один из узлов решетки выбрать за начало координат, то любой другой узел решетки определяет радиус-вектором R = ma + nb + pc, где m, n, p – три числа, которые называют индексами данного узла. Совокупность чисел m, n, p, записанная в двойных квадратных скобках [[m, n, p]], называется символом узла.
Символы рядов (ребер, направлений). Направление ряда определяется двумя точками: началом координат и любым узлом ряда. Символ этого узла принимают за символ ряда и пишут в квадратных скобках [u v w]. Координаты любого узла, принадлежащего направлению, выраженные в долях осевых единиц и приведенные к отношению трех целых наименьших чисел, и есть кристаллографические индексы направления.
4)Символы плоскостей (граней). Параметры Вейсса и индексы Миллера.
5)Закон целых чисел. Условия зональности.
Закон целых чисел. Закон целых чисел, установленный Гаюи, утверждает: для любых двух граней реального кристалла двойные отношения параметров равны отношению малых целых чисел, т.е. ОА’/OA : ОВ’/OB : ОС’/OC = p : q : r (1) где p, q, r – целые взаимно простые числа. Плоскость A’B’C’ может быть гранью кристалла только, если отрезки ОА’, ОВ’, ОС’, отсекаемые ею на осях координат, и «единичные» отрезки ОА, ОВ, ОС связаны соотношением (1).
Условия занальности. Грани кристалла, пересекающиеся по параллельным ребрам, образуют пояс или зону, а общее направление этих ребер называют осью зоны. Символ [u v w] характеризует ось зоны. uh+vk+wl=0 Если направление считать осью зоны, к которой принадлежат рассматриваемые плоскости (h1k1l1) и (h2k2l2)
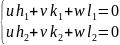


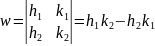
Две грани определяют ребро (ось зоны), два ребра (две зоны) — грань кристалла.
Возможные грани и ребра кристалла легко получить по четырем с известными символами граням, три из которых не пересекаются по параллельным ребрам (т. е. не принадлежат одной зоне), или по четырем ребрам, три из которых не лежат в одной плоскости.
Это положение отражает сущность закона Вейсса (1804 г.), или закона поясов (закона зон):
всякая плоскость, параллельная двум пересекающимся ребрам кристалла (принадлежащая двум его зонам), представляет собой возможную грань кристалла, а всякое направление, параллельное линии пересечения двух граней кристалла, — его возможное ребро.
книгаЧепаринФИЗЭМВ04 (Книга по Чепарину), страница 14
Описание файла
Документ из архива “Книга по Чепарину”, который расположен в категории “книги и методические указания”. Всё это находится в предмете “магнитные материалы и компоненты” из седьмого семестра, которые можно найти в файловом архиве МЭИ (ТУ). Не смотря на прямую связь этого архива с МЭИ (ТУ), его также можно найти и в других разделах. Архив можно найти в разделе “книги и методические указания”, в предмете “магнитные материалы и компоненты” в общих файлах.
Онлайн просмотр документа “книгаЧепаринФИЗЭМВ04”
Текст 14 страницы из документа “книгаЧепаринФИЗЭМВ04”
Физические величины и , как было показано ранее, связанные с обменным взаимодействием и молекулярными магнитными полями, определяют поведение ферримагнетика во внешнем магнитном поле. В связи с этим можно предположить, что существуют области значений коэффициентов и , при которых ферромагнетик будет находиться в парамагнитном состоянии при любой температуре.
Как показали исследования Нееля, любой ферримагнетик имеет асимптотическую температуру Кюри а, находящуюся в отрицательной области температур, поэтому можно предположить, что диапазон температур от а до Т=0 К любой феррит находится в парамагнитном состоянии.
Следовательно, принимая величины коэффициентов и за координаты, можно получить плоскость (, ), на которой при определенных граничных условиях можно определить кривую, отделяющую парамагнитную область ферримагнетика от ферромагнитной.
Эта кривая соответствует условию ТN=0, т.е. выражение (7.10) приравняем 0 и решим его при следующих условиях: поставим перед коренным выражением знак “минус”, а второй член подкоренного выражения равен нулю. При этих условиях получаем равнобочную гиперболу =1 в третьем квадранте.
На рис 7.3 показана плоскость с граничной кривой =1.
Рис. 7.3. Разбиение плоскости и типы кривых зависимости М от Т
для отрицательного взаимодействия А-В
В области влево и ниже от отрицательной ветви этой гиперболы подрешетки находятся в парамагнитном состоянии а 1. При этом направление векторов Ма и Mb будут параллельны или антипараллельны в зависимости от величины косвенного обменного взаимодействия между подрешетками.
При повышении температуры намагниченность обеих подрешеток будет уменьшаться до нуля при общей температуре Кюри.
Рассмотрим виды кривых М=f(Т) при отрицательном обменном взаимодействии между подрешетками. В этом случае поведение кривых температурной зависимости намагниченности определяется на плоскости величинами Ma и Mb.
В случае если при некоторой температуре суммарная намагниченность равна нулю, т.е. Ма+Mb=0, кривая М=f(T) характеризуется наличием так называемой точки компенсации (тип N). Другой тип Р кривой М=f(T) представляет собой зависимость с максимумом при некоторой температуре Т>0. Такая зависимость может быть объяснена тем, что намагниченность каждой подрешетки в зависимости от температуры будет изменяться в соответствии с величиной обменных взаимодействий. Если aa>bb, то при повышении температуры Мb уменьшается быстрее, чем Ма. В этом случае в определенном интервале температур расхождение между Ма и Mb будет возрастать так, что на кривой М=f(Т) появится максимум.
Следует отметить, что при выполнении условий aa>bb и 2+ и Fe 3+ в кристаллографических пустотах.
Октаэдрические узлы в химической формуле отмечают квадратными скобками. Учитывая это, можно записать формулу нормальной шпинели в виде Me 2+ [Fe2 3+ ]O4
В практике, такой структуре соответствуют составы Zn 2+ [Fe2 3+ ]O4, Cd 2+ [Fe2 3+ ]O4
Кристаллическая структура и кристаллическая решетка
Материальные частицы (атомы, ионы, молекулы), образующие кристаллическую структуру, располагаются в пространстве закономерно, периодически повторяясь в строго определенных направлениях, через строго определенные промежутки. Геометрической схемой, описывающей расположение материальных частиц в кристалле, является пространственная решетка (кристаллическая решетка). Она строится на трех основных некомпланарных трансляциях, или параметрах решетки: а, b, с. В зависимости от величин и взаимной ориентировки трансляций а, b, с, пространственные решетки имеют различную симметрию. Симметрия кристаллической структуры ограничивает число возможных решеток. Основные трансляции, а значит, и решетка, должны соответствовать симметрии структуры кристалла.
Выбор основных трансляций в структуре кристалла очень важен, потому что ими определяются кристаллографические системы координат. В анизотропной кристаллической среде удобно ориентироваться с помощью трехмерной системы координат, выбранной в соответствии с симметрией кристалла. В общем случае это косоугольные координаты с неодинаковыми масштабными отрезками по осям: a b c, 90 0 .
Следует помнить, что кристаллическая структура — это физическая реальность, а пространственная решетка — лишь геометрическое построение, помогающее выявить законы симметрии или наборы симметричных преобразований кристаллической структуры.
Точки пересечения трансляций, слагающих пространственную решетку, называются узлами. Узел может находиться как в промежутке между материальными частицами, так и в центре масс одной частицы или группы частиц. Если узел пространственной решетки символизирует группу частиц, то остальным узлам соответствуют такие же группы частиц.
Три элементарные трансляции решетки определяют элементарную ячейку, или параллелепипед повторяемости (рис.3). Существует множество способов выбора элементарной ячейки, но принято выбирать ее так, чтобы она соответствовала симметрии решетки.
Рис. 3. Пространственная решетка
Метод кристаллографического индицирования
Для описания кристаллических многогранников и структур применяется метод кристаллографического индицирования, удобный для всех кристаллографических систем координат независимо от того, прямоугольны они или косоугольны, одинаковые у них масштабные отрезки по осям или разные.
Рис. 10. Символы узлов в плоской сетке (а) и вершин, центра и центров гране куба (б)
Символы рядов (ребер)
Ряд, или узловая прямая, а также ребро кристаллического многогранника характеризуются наклоном в выбранной системе координат. Если ряд не проходит через начало координат, мысленно сдвинем его параллельно самому себе так, чтобы он прошел через начало координат. Мы всегда имеем право на такой параллельный перенос, потому что все параллельные направления в кристалле равнозначны. Тогда направление ряда определится двумя точками: началом координат и любым узлом ряда. Символ этого узла принимают за символ ряда и пишут в квадратных скобках [тпр]. Очевидно, этот символ характеризует семейство параллельных рядов, а также и параллельные ребра кристаллического многогранника.
Грани кристалла, пересекающиеся по параллельным ребрам, образуют пояс, или зону, а общее направление этих ребер называется осью зоны. Символ [тпр] характеризует ось зоны.
Рис. 11. Символы некоторых направлений в плоской сетке
Символы некоторых направлений в плоской сетке показаны на рис. 11,а. Из рис. 10 и 11 следует, что, например, ряд [110] можно характеризовать и символом [220], [330] и т. п., но для определения символа ряда принято выбирать узел, ближайший к началу координат. Если индексы в символе ряда кратные, их можно сокращать на целое положительное число.
Оси координат OX, OY, 01 имеют соответственно символы [100], [010], [001] (рис. 11,б). Здесь видно одно из основных преимуществ кристаллографической символики: символы осей координат не зависят от углов между осями координат и от осевых отрезков, они одинаковы в любой системе координат.
Символы плоскостей (граней)
Плоские сетки в пространственной решетке и соответствующие им грани кристаллического многогранника тоже характеризуются наклоном в заданной системе координат. Любая грань кристалла параллельна какой-либо плоской сетке, а значит, бесконечному числу параллельных ей плоских сеток.
Пусть некая плоскость решетки пересекает все три оси координат, отсекая на них отрезки та, пb, рс. Отношение чисел т : п : р характеризует наклон плоскости к осям координат. Таким же отношением определяется и ориентировка всего семейства параллельных ей плоскостей.
Так, для семейства плоскостей на рис. 12 имеем:
14Правила установки кристаллов различных сингоний.
15Индицирование граней кристаллов и простых форм. Параметры Вейсса и индексы Миллера
Установить кристалл означает правильно выбрать кристаллографические оси и единичную грань в соответствии с условными международными правилами установки.
Как уже говорилось, координатные оси, проведенные параллельно рядам пространственной решетки называются кристаллографическими осями.
Как известно, вдоль рядов кристаллической решетки проходят действительные или возможные ребра кристаллических многогранников.
Поскольку в кристаллографии все параллельные направления идентичны, точка O– точка пересечения ребер, мысленно перенесенных параллельно самим себе в центр кристалла, принимается за начало координат. Направление на наблюдателя (OX) принимается за I кристаллографическую ось, OY – вправо от наблюдателя – за II кристаллографическую ось и OZ – вертикально вверх – за III кристаллографическую ось.
Правила выбора осей координат в кристаллах
1. Оси координат следует совмещать с осями симметрии, отдавая предпочтение осям симметрии высшего порядка. Единственную ось симметрии высшего порядка следует совмещать с осью Ζ. В кристаллах моноклинной сингонии единственную ось L2 следует совмещать с осью Y.
2. Координатные оси следует располагать перпендикулярно плоскостям симметрии кристалла при отсутствии осей симметрии.
3. Координатные оси следует проводить параллельно наиболее развитым ребрам кристалла при отсутствии осей и плоскостей симметрии.
4. Оси координат должны пересекаться в геометрическом центре кристалла
16. Закон целых чисел (Гаюи)
Второй закон клисталлографии.
Отношение отрезков, отсекаемых двумя гранями кристалла на координатных осях( или на трех пересекающихся ребрах) относятся друг к другу как целое, взаимно простые и малые числа. Для сравнения между собой параметров граней кристалла одна из его граней принимается за масштабную. Ее называют единичной гранью. При измерении положения других граней изучаемого кристалла параметры это грани принимают за единицу.
17. Закон постоянства двугранных углов(Стено).
закон постоянства углов кристаллов, утверждает, что во всехкристаллах данного вещества при данных температуре и давлении двугранные углы между соответствующими гранями кристаллов (вне зависимости от размеров и формы граней) всегда одинаковы. Установлен Н. Стено в 1669 на основании наблюдения многогранных форм природных кристаллов и объясняется тем, что грани кристаллического многогранника соответствуют плоским атомным сеткам в кристаллической решётке. С. з. лежал в основе классификации и определения кристаллических веществ (измерение углов с помощью гониометра).
26) Координационные числа и координационные многогранники.
Координационным числом данного атома называется число ближайших однотипных соседних атомов (для иона – число ближайших окружающих ионов противоположенного знака). Расположение атомов и число соседей зависят с одной стороны, от отношения их размеров и, с другой от направления и числа связей. В соединениях с ненапрваленой связью на перовм месте стоят соотношения размеров ( катионов и анионов; в металлической связи размеры равны). Число анионов, с которыми может быть одновременно установлен контакт, зависит от относительных радиусов катионов и анионов ( отношения их радиусов)
Если ближайшие атомы или ионы соединить линиями, то получится координационный многогранник (полиэдр КП)
Координационные многогранники-полиэдры соединяются между собой различными способами: через промежуточные ионы металлов,путем обобществления вершин или ребер. Соединение полиэдров по ребру или грани энергетически невыгодно ( сближение центральных катионов по ребру и возрастание отталкивания их) поэтому редко встречаются. Координационные многогранники вокруг маленьких катионов с более высоким зарядом соединяются только вершинами, с небольшим зарядом- могут ребрами и иногда даже гранями.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Дифракционные методы анализа
соединяющие нулевой атом с неидентичными атомами, расположенными внутри элементарной ячейки или на её гранях.
Для того, чтобы выделить в структуре элементарную ячейку Бравэ, нужно, согласно правилам выбора элементарной ячейки, найти три кратчайшие некомпланарные трансляции а, b, с, которые обязательно должны соединять одинаковые узлы. Полученную элементарную ячейку необходимо проверить:
1. Можно ли на этих трансляциях построить ячейку, отвечающую правилам выбора ячейки Бравэ?
2. Все ли частицы в структуре можно получить с помощью такого выбора трансляций?
Согласно этим требованиям, элементарная ячейка описывается базисом.
Базисом называется совокупность координат неидентичных атомов, входящих в элементарную ячейку. Атомы идентичны, если они химически одинаковы и структурно эквивалентны (т.е. их положение в структуре эквивалентно при заполнении бесконечного кристаллического пространства с помощью элементарной ячейки). Если атомы химически неодинаковы или структурно неэквивалентны, они называются
неидентичными. Например, в чистых кристаллических веществах, имеющих ОЦК решётку, в элементарной ячейке содержится два неидентичных атома, которые химически одинаковы, но имеют разное положение в структуре. Атомы одного типа располагаются в вершинах элементарной ячейки и принадлежат одновременно 8-ми ячейкам.
Следовательно, на одну элементарную ячейку приходится
координатами [[000]]. Второй с координатами [[ 1 2 1 2 1 2 ]] находится в центре
элементарной ячейки. Таким образом, базис ОЦК решётки чистого вещества записывается как [[000; 1 2 1 2 1 2 ]].
Если рассматривать расположение атомов NaCl, то атомы Na и Cl располагаются в плоскостях <100>в шахматном порядке, причем в соседних плоскостях этого типа атомы натрия чередуются с атомами хлора. Обычно такое чередование атомов в решётке описывается элементом решётки, как показано на рис.1.10.
Рис. 1.10. Элемент решетки NaCl: 

Однако этот элемент решётки NaCl
не является элементарной ячейкой,
поскольку его нельзя транслировать в пространстве. Для возможного
транслирования в пространстве необходимо увеличить трансляции по осям Х,
У, Z таким образом, чтобы с помощью полученной элементарной ячейки можно
было описать все бесконечное пространство решётки NaCl: по осям Х, У и Z
нужно удвоить расстояние между атомами, которые будут соединять между
собой химически одинаковые атомы согласно закону их чередования в
структуре. Эти расстояния и будут периодами кристаллической решётки NaCl,
а элемент пространства – элементарной ячейкой NaCl, содержащей 8 ячеек
(рис.1.10), в которой показано чередование атомов в трёхмерном пространстве
и которуюможно транслировать по осям координат (рис.1.11).
Рис. 1.11. Элементарная ячейка решетки NaCl:
После определения базиса решётки становится возможным описание
положения узлов, направлений и плоскостей в решётке (рис.1.12).
Любой узел решётки определяется радиус-вектором
соединяющим выбранный за нулевой узел с данным узлом.
Ряд или узловая прямая в решётке, а также ребро кристаллического многогранника характеризуются наклоном в выбранной системе координат. Если ряд не проходит через начало координат, он проводится параллельно самому себе через начало координат.
Рис. 1.12. Положения узлов [[ХУZ]] в решетке
символе ряда кратные, их необходимо сокращать на целое положительное число.
Любая грань кристалла или плоскость, проведенная через узлы пространственной решётки, параллельна какой-либо плоской сетке, а значит бесконечному числу плоских сеток.
2-я плоскость а 2 3 b ∞ и т.д., то полученные соотношения будут 1 2 : 1 3 : ∞ = 1: 2 3 : ∞
В кристаллографии принято характеризовать плоскости или нормали к ним не параметрами, а индексами Миллера. Индексы Миллера – это величины, обратные параметрам Вейсса, приведённые к целым числам. Если параметры плоскости p,q,r (отрезки, отсекаемые плоскостью по осям координат), то индексы Миллера определяются из соотношения:
В приведённом примере h : k : l = 1 p : 1 q : 1 r = 1 3 : 1 2 : 1/∞ = 2 : 3 : 0.
Числа h,k,l называются индексами плоскости; индексы, написанные подряд и заключённые в круглые скобки ( hkl ), называются символом плоскости.
Символом ( hkl ) характеризуется вся совокупность параллельных плоскостей. Этот символ означает, что система параллельных плоскостей
рассекает отрезок а на h частей, отрезок в на k частей и отрезок с на l частей, т.е. величины h,k,l обратно пропорциональны отрезкам, отсекаемым этой плоскостью на осях координат. Все плоскости данного семейства обозначаются фигурными скобками: < hkl >. Если индексы в символе ряда кратные, их необходимо сокращать на целое положительное число (рис.1.13).
Оси координат имеют символы: ОХ – [100], ОУ – [010], OZ – [001]. Символы осей координат не зависят от углов между осями координат и от
осевых отрезков, они одинаковы в любой системе координат.
В общем виде уравнение плоскости записывается как
где N – всегда целое число;
h,k,l – взаимно простые, целые числа.
Для плоскости, проходящей через начало координат, N = 0, для плоскости, ближайшей к началу координат, N=1.
1. Найти символы плоскости, отсекающей на осях координат отрезки
Пишем соотношение m:n:p = 4:3:2
2. Найти символы плоскости, параллельной осям X, Z и отсекающей 3 единицы на оси У.
Символы координатных плоскостей, независимо от углов между осями координат, всегда будут:
Х0У = (001), Х0Z = (010), У0Z = (100).
Каждое семейство направлений и плоскостей < hkl >, в котором все индексы имеют разные значения, содержит 48 разных вариантов [ uvw ] или
( hkl ), тогда как в семействах uvo > и < hko >− их 24, в семействах uuu > и < hhh >– 8, в и < hho >–12, в семействах uoo > и < hoo >– 6.
Рис. 1.13. Элементарная ячейка примитивной кубической решетки:
Если же в результате термообработки, например, отжига, в решётке фазы происходит упорядочение атомов таким образом, что атомы разных сортов располагаются слоями в плоскостях (001), то решётка изменит симметрию с кубической на тетрагональную. Элементарная ячейка такой тетрагональной решётки будет состоять из двух кубических ячеек и описываться базисом
Рис. 1.14. Элементарная ячейка упорядоченной фазы состава АВ:


координатах, будет иметь индексы (112), а положение плоскости (111) займет положение плоскости (221) неупорядоченной решётки, а направление [111] упорядоченной решётки будет иметь индексы [112] в старых координатах.
Метод описания плоскостей или направлений (граней и рёбер) кристалла с помощью индексов и символов основывается на законе целых чисел или законе рациональности параметров.
За оси координат выбираются направления трех непараллельных рёбер кристалла, а за единицы измерения (периоды) по этим осям – отрезки, отсекаемые на них какой-либо гранью кристалла, принятой за “единичную”. Пусть “единичная” грань отсекает на осях координат отрезки ОА, ОВ, ОС
Рис. 1.15. Параллельные грани в кристалле
где p,q,r – целые, взаимно простые и для реальных кристаллов малые (не превышающие значения, равного 5) числа.
Плоскость A ′ B ′ C ′ может быть гранью кристалла, только если отрезки
Кристалл растёт так, что частицы вещества из окружающей среды отлагаются на его гранях. Грани нарастают параллельно самим себе. Меняются площади граней, их форма, но взаимный наклон граней остаётся неизменным, поэтому углы между плоскостями тоже остаются постоянными. В этом заключается закон постоянства углов: во всех кристаллах данного вещества при одинаковых условиях (т.е. при одинаковых температуре и давлении и при одинаковой модификации кристаллической решётки) углы между соответствующими плоскостями кристаллов постоянны.
Согласно закону постоянства углов, характерными параметрами любого кристаллического вещества являются углы между плоскостями (или гранями) кристалла, которые остаются неизменными до тех пор, пока устойчива кристаллическая структура. Форму кристаллического многогранника, расположение его элементов симметрии, анизотропию свойств можно характеризовать набором углов между плоскостями (гранями) кристалла. Символы плоскостей (граней) и направлений (рёбер) кристалла удобно изображать и определять с помощью кристаллографических проекций.
В заключение приведены три примера расшифровки записей пространственных групп структур, принадлежащих низшей, средней и высшей категориям:
1. Пространственная группа Р 222 описывает кристаллическую структуру, принадлежащую ромбической сингонии, поскольку в ней нет осей, порядок n которых больше 2, а есть три оси второго порядка, параллельные осям X, У и Z,