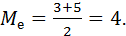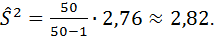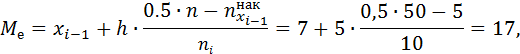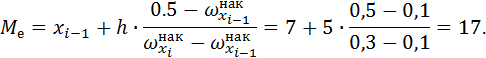Найти точечные параметры выборки двумя способами
Точечные характеристики выборки (оценки параметров)
К точечным оценкам предъявляются требования несмещенности, состоятельности и эффективности.
Оценка 


Оценка 


Эффективной называется та оценка, которая имеет наименьшую дисперсию среди других возможных оценок.
Рассмотрим эти оценки.




Выборочная дисперсия не удовлетворяет свойству несмещенности, поэтому вводится также исправленная выборочная дисперсия

Желательно в качестве меры рассеяния иметь характеристику, выраженную в тех же единицах, что и варианты. Поэтому вводится среднее выборочное квадратическое отклонение:

Рассматривается также безразмерная характеристика – коэффициент вариации, который служит для оценки однородности опытных данных:
Мода 
Медиана 


Для дискретного ряда из нечетного числа членов медиана равна серединной варианте, для ряда из четного числа членов – полусумме двух серединных вариант.
Выборочные характеристики и точечные оценки



ÆВыборочными характеристиками называются функции от наблюдений, приближённо оценивающие соответствующие числовые характеристики случайной величины.
Оценки параметров генеральной совокупности делятся на два класса: точечные и интервальные.
Точечныеоценки выражаются одним числом (точкой на числовой оси), находятся такие оценки по данным выборки и используются в дальнейшем вместо оцениваемого параметра. Точечная оценка, как функция от выборки, является случайной величиной и меняется от выборки к выборке при повторном эксперименте.
Интервальные оценки определяются двумя числами – концами интервала, который накрывает оцениваемый параметр.
В отличие от точечных оценок, которые не дают представления о том, как далеко от них может находиться оцениваемый параметр, интервальные оценки позволяют установить точность и надёжность оценок.
Если объём выборки 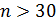
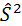
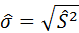
К точечным оценкам предъявляют требования, которым они должны удовлетворять, чтобы хоть в каком-то смысле быть «доброкачественными». Это несмещённость, эффективность и состоятельность [1].
В качестве точечных оценок математического ожидания, дисперсии и среднего квадратического отклонения используют выборочные характеристики соответственно выборочное среднее, выборочная дисперсия и выборочное среднее квадратическое отклонение:
1) выборочное среднее: 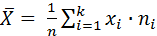
2) выборочная смещённая (неисправленная) дисперсия:
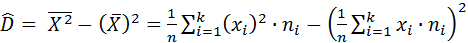
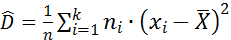
3) выборочная несмещённая (исправленная) дисперсия:
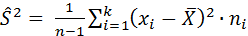
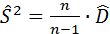
4) смещённое выборочное среднее квадратическое отклонение:
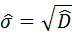
5) несмещённое выборочное среднее квадратическое отклонение:
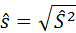
Þ Примечание. Выборочное среднее 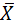
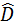
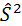
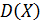
В качестве других используемых на практике выборочных характеристик можно назвать выборочную моду 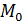
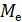
Для наблюдений дискретной случайной величины:
— выборочная мода 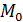
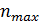
— выборочная медиана 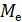
— есличисло наблюдаемых вариант есть чётное число, тогда выборочная медиана 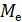
Медиана 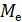
В том случае, когда наблюдения проводятся для непрерывной случайнойвеличины, то мода 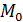
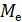
Что касается моды 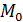
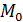
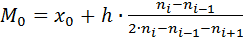
здесь 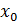
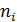
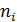
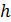
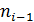
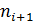
Медиану определяем по следующему алгоритму:
1) найдите медианный интервал 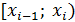
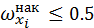
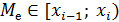
2) вычислите медиану 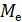
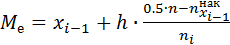
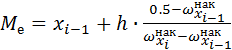
здесь 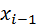
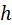
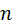
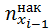
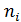
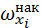
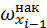
?Упражнение 3. Найдите выборочное среднее, смещённую и несмещённую выборочные дисперсии, смещённое и несмещённое выборочные средние квадратические отклонения, моду 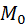
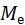
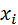 |
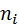 |
В упражнении рассматривается дискретная случайная величина. Вычисления выполним в MS Excel.
Þ Примечание. В данном примере чётное количество вариант, а именно 4, это 2, 3, 5, и 6. Поэтому медиану определяем как среднее значение дух серединных элементов:
Несмещённая выборочная дисперсия вычисляется по формуле:
?Упражнение 4. Найдите выборочное среднее, выборочную дисперсию (смещённую и несмещённую), выборочное среднее квадратическое отклонение (смещённое и несмещённое) по данному распределению выборки:
| Частичный интервал | [2,7) | [7,12) | [12,17) | [17,22) | [22,27) |
Число наблюдений, попавших в интервал, 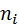 |
В данном упражнении наблюдения выполнены для непрерывной случайной величины. Здесь обязательно надо найти середины исследуемых интервалов. Именно таким образом поставленную задачу сведём к исследованию дискретной случайной величины. Вычисления выполним в MS Excel.
| Частичный интервал | Частота 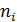 | Относитель- ная частота 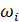 | Накоплен-ная относительная частота 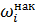 | Начало интервала | Конец интервала | Середина интервала | Произведе- ние середины интервала на частоту |
| [2; 7) | 0,1 | 0,1 | 4,5 | 22,50 | |||
| [7; 12) | 0,2 | 0,3 | 9,5 | 95,00 | |||
| [12; 17) | 0,5 | 0,8 | 14,5 | 362,50 | |||
| [17; 22) | 0,12 | 0,92 | 19,5 | 117,00 | |||
| [22; 27) | 0,08 | 24,5 | 98,00 | ||||
| Объём выборки: | 695,00 | ||||||
| Длина интервала: | Выборочное среднее: | 13,90 | |||||
| Мода М0: | 14,21 | ||||||
| Медиана Ме: | 17,00 |
Интервал [7; 12) является медианным интервалом, поскольку накопленная относительная частота равна 0.3, а это значение меньше, чем 0.5, т. е. 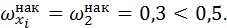
— выборочную дисперсию (смещённую и несмещённую оценки);
— выборочное среднее квадратическое отклонение (смещённую и несмещённую оценки), для чего выполним дополнительные вычисления.
Найти точечные параметры выборки двумя способами
1. Задачи математической статистики.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров распределения.
9. Интервальные оценки параметров распределения.
1. Задачи и методы математической статистики
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным- контролируемый размер детали.
Иногда проводят сплошное исследование, т.е. обследуют каждый объект относительно нужного признака. На практике сплошное обследование применяется редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (выборочную совокупность) и подвергают их изучению.
Основная задача математической статистики заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е. изучение вероятностных свойств совокупности: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов.
Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.
При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки делятся на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.
В американском журнале «Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов относительно исхода предстоящих выборов президента США в 1936 году. Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве источника для генеральной совокупности исследуемых американцев были взяты справочники телефонных абонентов. Из них случайным образом были выбраны 4 миллиона адресов., по которым редакция журнала разослала открытки с просьбой высказать свое отношение к кандидатам на пост президента. Обработав результаты опроса, журнал опубликовал социологический прогноз о том, что на предстоящих выборах с большим перевесом победит Ландон. И … ошибся: победу одержал Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная часть населения, которые поддерживали взгляды Ландона.
На практике применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует расчленения генеральной совокупности на части (а) простой случайный бесповторный; б) простой случайный повторный).
2. Отбор, при котором генеральная совокупность разбивается на части. (а) типичный отбор; б) механический отбор; в) серийный отбор).
Простым случайным называют такой отбор, при котором объекты извлекаются по одному из всей генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типичной» части. Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных «типичных» частях генеральной совокупности.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой отбор может не обеспечивать репрезентативность выборки (если отбирают каждый 20-ый обтачиваемый валик, причем сразу же после отбора производится замена резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4. Статистическое распределение выборки
Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный вариационный ряд частот может быть представлен таблицей: