Нелинейная регрессия оценка параметров

Машинное обучение — 2. Нелинейная регрессия и численная оптимизация

Прошел месяц с появления моей первой статьи на Хабре и 20 дней с момента появления второй статьи про линейную регрессию. Статистика по просмотрам и целевым действиям аудитории копится, и именно она послужила отправной точкой для данной статьи. В ней мы коротко рассмотрим пример нелинейной регрессии (а именно, экспоненциальной) и с ее помощью построим модель конверсии, выделив среди пользователей две группы.

Итак, вот данные, которые будем использовать в качестве примера. Пики посещаемости (ряд Views, красный пунктир) приходятся на моменты выхода статей. Второй ряд данных (Regs, с множителем 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание Mathcad Express – с его помощью, к слову, вы сможете повторить все расчеты этой и предыдущих статей). Все картинки — это скриншоты Mathcad Express, а файл с расчетами вы можете взять здесь.

Зеленой стрелкой на графике я обозначил фрагмент данных, для которого мы будем строить нелинейную регрессию. Согласно модели, которую мы примем за основу, после короткого переходного периода после выхода публикации, количество просмотров уменьшается со временем приблизительно по экспоненциальному закону:
Views ≈ C₀∙exp(C₁∙t).
Обоснование этой модели пока отложим до одной из будущих статей, когда речь пойдет о пуассоновском случайном процессе.

Понятно, что для анализа нужно выбрать тот фрагмент, который соответствует модели (на слишком близко к начальному пику и без суммирования со статистикой посещений после выхода второй статьи). Именно этот промежуток выделен зеленой стрелкой на первом графике, а в более крупном масштабе он выглядит вот так:

Экспоненциальная регрессия, напомню, определит график такой экспоненциальной функции, который будет «в среднем» ближе всего располагаться к показанным экспериментальным точкам. Для того чтобы найти коэффициенты регрессии, необходимо будет решить оптимизационную задачу на отыскание минимума целевой функции:

(T,Y) – массив из N экспериментальных точек, а множитель мы ввели для удобства (он не влияет на положение минимума). Дальше, конечно, можно было бы сразу написать одну-две строчки кода со встроенной функцией поиска минимума для получения искомых С0 и С1, однако, мы используем бесплатный Mathcad Express, где все они выключены, поэтому пойдем чуть более громоздким (зато более простым для понимания и наглядным) путем.
Для начала, посмотрим, как ведет себя функция R(c0, c1). Для этого зафиксируем несколько значений с0 и построим для каждого из них график функции одной переменной R(c0, х).

Видно, что для выбранных с0 любой из графиков семейства имеет один минимум, положение которого х зависит от с0, т.е. можно записать x=g(c0). Самый глубокий минимум, т.е., минимум R(c0, g(c0))

min будет искомым глобальным минимумом. Его-то нам и надо найти для решения задачи. Чтобы найти глобальный минимум, сначала (средствами, доступными в Mathcad Express) определим пользовательскую функцию g(y), а потом найдем минимум R(y, g(y)).

Не буду останавливаться на численном алгоритме вычисления минимума (кому интересно, он приведен в первой строчке следующего скриншота). Решение задачи (точка, в выбранных обозначениях с0=y0 и с1=х0), значение целевой функции в этой точке и график регрессии приведен ниже:

Обратите внимание на то, что значение целевой функции в минимуме (т.е. сумма квадратов невязок) снижается по сравнению со случаем с2=0 больше, чем на порядок!
В заключение, приведу результат работы встроенной функции expfit для нахождения экспоненциальной регрессии (имеющейся в коммерческой версии Mathcad Prime). Результат работы показан на графике зеленым пунктиром, а наш результат (тот же, что и на предыдущем графике) – красной сплошной линией.

Все картинки — это скриншоты Mathcad Express (сами расчеты можете взять здесь, повторить, а при желании изменить и использовать для своих нужд). Не забудьте в начале расчетов задать с2=0 или с2=150, чтобы выбрать первую или вторую модель соответственно.

Источник

Оценка параметров регрессий нелинейных регрессий

Σy*x=a*Σx+b* Σx 2 +c* Σx 3

Σy*x 2 =a* Σx 2 +b* Σx 3 +c* Σx 4

В классе нелинейных функций, параметры которых без особых затруднений оцениваются МНК, в эконометрике хорошо известна равносторонняя гипербола у=а+b/х. если в уравнении равносторонней гиперболы у=а+ b/х+Е заменить 1/х на z, получим линейное уравнение регрессии у=а+b*z+Е, оценка параметров которого может быть дана МНК. Система нормальных уравнение имеет вид: Σу=n*a+b*Σ1/x

Во всей этой деятельности существенным является использование моделей. В большинстве случаев экономические законы выражаются в относительно простой математической форме. Рассмотрим, например, функцию потребления

У – потребление товара А;

Х₁ – индекс цен на продукцию;

Х₂ – доход на душу населения.

Данная функция описывает в среднем поведение потребителя по отношению к покупке данного товара. Закон поведения будет найден, как только мы найдем значения коэффициентов В и С. Задача эконометрики в этом случае – определить (оценить) эти коэффициенты из подходящего набора наблюдений. Но это не единственная задача, здесь могут возникнуть и другие вопросы:

— нет ли переменных, которые следовало бы дополнительно включить в уравнение (или исключить);

— насколько корректно измерены наши данные (доход, индекс цен). Если они не отражают того, что должны отражать, то поведенческая модель потребителя теряет смысл;

— верно ли, что модель линейна;

— что нужно изучать: макроэкономическое уравнение (данные на уровне областей, регионов) или микроэкономическое ( индивидуальные данные по конкретным людям);

— является модель статической, когда используют данные одного периода, или динамической, поскольку спрос данного года может определяться не только доходом текущего периода, но и прошлых лет?

Эконометрика рассматривает эти и многие другие возникающие вопросы и предлагает способы решения названных проблем.

50.Нелинейная регрессия. Методы линеаризации.Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др. Различают два класса нелинейных регрессий: 1)регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; 2)регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: 1)полиномы разных степеней –у = а +bх + с2 + ε, у = а + bх +сх +dx3+ ε; 2)равносторонняя гипербола К нелинейным регрессиям по оцениваемым параметрам относятся функции: 1)степенная — y = axbε; 2)показательная – у = аbх ε; 3)экспоненциальная – y=ea+bxε. Приведение к линейному виду регрессий, нелинейных по объясняющим переменным. Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени у= а0 + а1 х + а2 х2 + ε заменяя переменные х1 =х, х2 = х2, получим двухфакторное уравнение линейной регрессии: у= а0 + а1 х1 + а2 х2 + ε для оценки параметров которого, как будет показано далее, используется МНК. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу Для равносторонней гиперболы такого вида, заменив на z, получим линейное уравнение регрессии y = a +bz +ε оценка параметров которого может быть дана МНК. Она может быть использована не только для характеристики связи удельных расходов сырья,материалов,топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроуровне, но и на макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у. В отдельных случаях может использоваться и нелинейная модель вида так называемая обратная модель, являющаяся разновидностью гиперболы Но, если в равносторонней гиперболе преобразованию подвергается объясняющая переменная z = 1/x и y = а + bz + ε, то для получения линейной формы зависимости в обратной модели преобразовывается у, а именно: z =1/y и z = a + bx +ε. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин 1/у, а именно следовательно полученная методом наименьших квадратов оценка уже не будет эффективной. Приведение к линейному виду регрессий, нелинейных по параметрам.Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция: y = axbε, где у – спрашиваемое количество; х – цена; ε – случайная ошибка. Данная модель нелинейна относительно оцениваемых пaраметров, ибо включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: lпу = lпа + b lnx + ln ε. Соответственно оценки параметров а и b могут быть найдены МНК. Если же модель представить в виде y = axbε, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. Внутренне нелинейной будет и модель вида — у = а + bхc + ε, ибо это уравнение не может быть преобразовано в уравнение, линейное по коэффициентам. В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель y = еa+bхε, ибо логарифмируя ее по натуральному основанию, получим линейную форму модели: lnу = а + b х +lnε. Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция y = axbε. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия , то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. lпу, 1/у. Так, в степенной функции y = axbε МНК применяется к преобразованному уравнению lпу = lnа + xlnb. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах: .Вследствие этого оценки параметров для линеаризуемых функций МНК оказываются несколько смещенными. При исследовании взаимосвязей среди функций, использующих ln у, в эконометрике преобладают степенные зависимости – это и кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости.

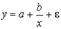
60. Коэффициент частной корреляцииизмеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

Источник

Виды нелинейной регрессии. Оценка параметров модели

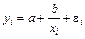
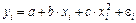
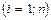
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций, например равносторонней гиперболы: ; параболы второй степени: и др.

Различают два класса нелинейных регрессий:

· относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

· по оцениваемым параметрам.

Рассмотрим нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам.

Данный класс нелинейных регрессий включает уравнения, в которых у линейно связан с параметрами. Примером могут служить следующие функции.

1. Полиномы разных степеней. Например, полином k-й степени .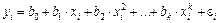

2. Равносторонняя гипербола – .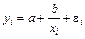

При оценке параметров регрессий нелинейных по объясняющим переменным используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

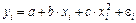
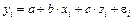
Рассмотрим применение данного подхода к параболе второй степени: . Заменяя переменную х 2 на z, получим двухфакторное уравнение линейной регрессии: , для оценки параметров которого используется обычный МНК.

Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: 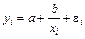. Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции.

Для оценки параметров равносторонней гиперболы используется тот же подход «замены переменных»: заменив 1/х на z, получим линейное уравнение регрессии: 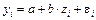, для которого может быть применен обычный МНК.

Регрессии нелинейные по оцениваемым параметрам. К данному классу регрессий относятся уравнения, в которых у нелинейно связан с параметрами. Примером таких нелинейных регрессий являются функции:

· степенная – ;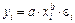

· показательная – ;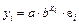

· экспоненциальная – .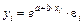

Данный класс нелинейных моделей подразделяется на два типа:

1) нелинейные модели внутренне линейные;

2) нелинейные модели внутренне нелинейные.

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен:

где у – спрашиваемое количество;

e – случайная составляющая.

Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: 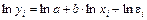. Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.

В рассматриваемой выше степенной функции предполагалось, что случайная составляющая u мультипликативно связана с объясняющей переменной х. Если же модель представить в виде 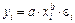, то она становится внутренне нелинейной, т. к. ее невозможно преобразовать к линейному виду.

Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Применение МНК для оценки параметров нелинейных моделей внутренне линейных. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. В таких моделях преобразованию подвергается результативный признак у, в отличие от нелинейных моделей 1-го типа, где результативный признак у остается неизменным, а преобразуется факторный признак.

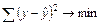
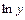
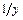
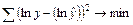
Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия , то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. , . Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений логарифмов:

. (23)

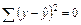
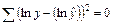
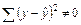
Соответственно, если в линейных моделях и моделях, нелинейных по переменным, , то в моделях, нелинейных по оцениваемым параметрам, , а . Вследствие этого оценка параметров с помощью МНК для нелинейных моделей, внутренне линейных, оказывается несколько смещенной.

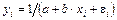
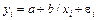
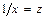
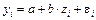
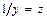
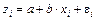
В отдельных случаях может использоваться так называемая обратная функция: , являющаяся разновидностью гиперболы. Но если в равносторонней гиперболе , преобразованию подвергается объясняющая переменная и , то для получения линейной формы зависимости в обратной модели преобразовывается у: . Тогда модель обратной зависимости принимает вид: .

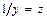
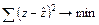
Обратная модель является внутренне линейной по параметрам. Требование МНК при этом выполняется для обратных значений результативного признака – , а именно: .

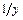
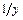
Поскольку уравнение обратной функции линейно относительно величин , то, если обратные значения имеют экономический смысл, коэффициент регрессии интерпретируется так же, как в линейном уравнении регрессии. Если, например, под у подразумеваются затраты на рубль продукции, а под х – производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу, и параметр b имеет экономическое содержание – средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.

1.3. Коэффициент эластичности как
характеристика силы связи фактора с результатом

Коэффициент эластичности представляет собой показатель силы связи фактора x с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1 %. Коэффициент эластичности (Э) рассчитывается как относительное изменение у на единицу относительного изменения x:

. (24)

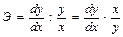
Различают обобщающие (средние) и точечные коэффициенты эластичности.

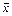
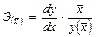
Обобщающий коэффициент эластичности рассчитывается для среднего значения : и показывает, на сколько процентов изменится у относительно своего среднего уровня при росте х на 1 % относительно своего среднего уровня.

Точечный коэффициент эластичности рассчитывается для конкретного значения х = х₀: 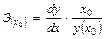и показывает, на сколько процентов изменится у относительно уровня у(х₀) при увеличении х на 1% от уровня х₀.

В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы приведены в табл. 2.

Вид функции	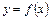Точечный коэффициент эластичности	Средний коэффициент эластичности
Линейная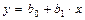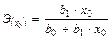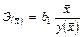
Парабола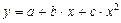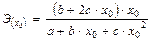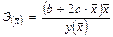
Равносторонняя гипербола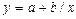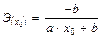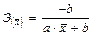
Степенная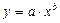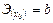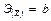
Показательная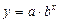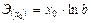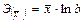
Полулогарифмическая у = a + b ∙ lnx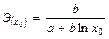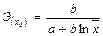

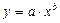
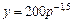
Только для степенных функций коэффициент эластичности представляет собой постоянную независящую от х величину (равную в данном случае параметру b). Именно поэтому степенные функции широко используются в эконометрических исследованиях. Параметр b в таких функциях имеет четкую экономическую интерпретацию – он показывает процентное изменение результата при увеличении фактора на 1 %. Так, если зависимость спроса у от цен p характеризуется уравнением вида: , то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,5 %.

Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, бессмысленно определять, на сколько процентов изменится заработная плата с ростом возраста рабочего на 1%. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наибольшего значения R 2 ), не может быть экономически интерпретирована.

Источник