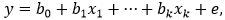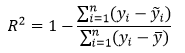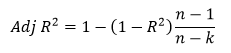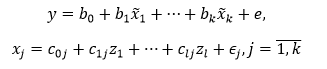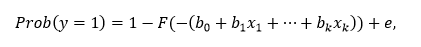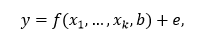Неверно что к свойствам оценок параметров классической линейной регрессионной модели относят ответ

ОТветы на синергию. Эконометрика. Автокорреляционная функция это функция от Тип ответа

Модель авторегрессии первого порядка

Обобщенный метод наименьших квадратов

Постоянство дисперсии случайного члена регрессионного уравнения

Отсутствие зависимости между остатками текущих и предыдущих наблюдений

Процесс не является стационарным в широком смысле

Показатель, характеризующий тесноту линейной стохастической связи между переменными

Явление линейной стохастической связи между переменными

Показатель, позволяющий установить факт наличия линейной

стохастической связи между переменными

Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Статистической значимости модели в целом

Статической зависимости каждого из коэффициентов модели

Определения статической значимости каждого коэффициента уравнения

Наличие линейной зависимости между несколькими объясняющими переменными

Дисперсии коэффициентов регрессии

Числа структурных коэффициентов над числом приведенных

О мультиколлинеарности факторов

Значение коэффициента равно нулю

С ростом Х происходит убывание У

Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной

Ранговое условие и порядковое условие со знаком равенства

Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными

Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

Положительные и отрицательные

Эндогенных переменных минус единица

Отбор факторов, влияющих на результат и выбор вида уравнения

Парные и множественные

Необходимым и достаточным

Системы минус единица

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Проверки статистической значимости фактора

Можно рассматривать в узком и в широком смысле

Характеристика временного ряда, связанная с его стабильностью

Качество уровня регрессии в целом

По нормальному закону

Качество уравнения регрессии в целом

Ее математическое ожидание не равно ей

Связь между переменными, сложенная влиянием случайных факторов

Обладают свойством гетероскедастичности

Источник

Оценка параметров линейного регрессионного уравнения

Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

В итоге получаем систему нормальных уравнений:

Эту систему можно записать в виде:

_{Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:}

_{В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.}

_{Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:}

_{где – коэффициент регрессии в уравнении связи;}

– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

_{Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.}

_{Зависимость между размером страховых возмещений и страховой суммой на автотранспорт}

_{Объем страхового возмещения (тыс.долл.), Yi}

_{Стоимость застрахованного автомобиля (тыс.долл.), X i}

Источник

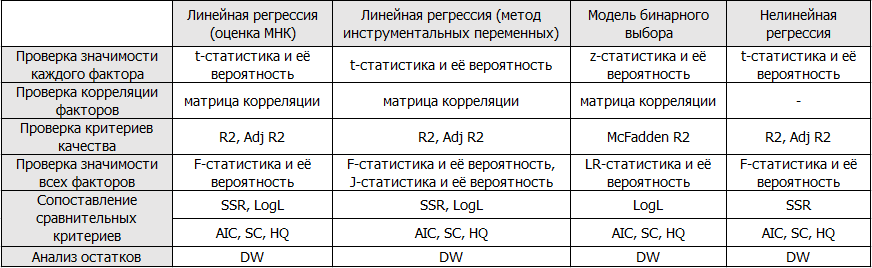
Критерии оценки качества регрессионной модели, или какая модель хорошая, а какая лучше

В данной статье мы поговорим о том, как понять, качественную ли модель мы построили. Ведь именно качественная модель даст нам качественные прогнозы.

Инструмент «Моделирование и прогнозирование» Prognoz Platform обладает обширным списком моделей для построения и анализа. Каждая модель имеет свою специфику и применяется при различных предпосылках.

Объект «Модель» позволяет построить следующие регрессионные модели:

Начнём с модели линейной регрессии. Многое из сказанного будет распространяться и на другие виды.

Модель линейной регрессии (оценка МНК)

Под моделью линейной регрессии будем понимать модель вида:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели.

Итак, куда смотреть?

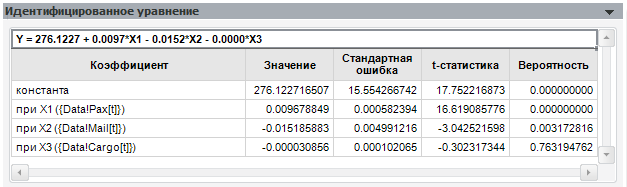
Для каждого коэффициента на панели «Идентифицированное уравнение» вычисляется ряд статистик:

Последняя является наиболее универсальной и показывает, с какой вероятностью удаление из модели фактора, соответствующего данному коэффициенту, не окажется значимым.

Открываем панель и смотрим на последний столбец, ведь он – именно тот, кто сразу же скажет нам о значимости коэффициентов.

Факторов с большой вероятностью незначимости в модели быть не должно.

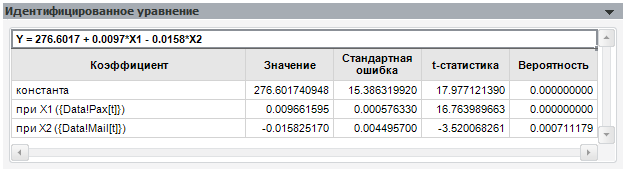
Как вы видите, при исключении последнего фактора коэффициенты модели практически не изменились.

Возможные проблемы: Что делать, если согласно вашей теоретической модели фактор с большой вероятностью незначимости обязательно должен быть? Существуют и другие способы определения значимости коэффициентов. Например, взгляните на матрицу корреляции факторов.

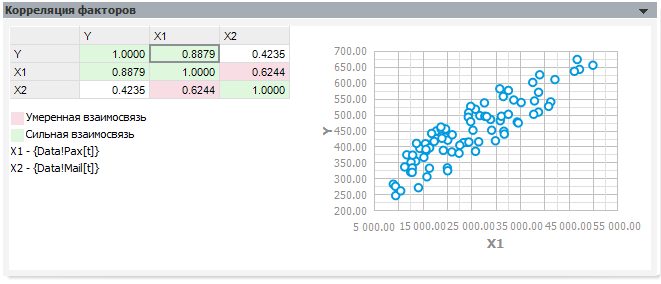
Панель «Корреляция факторов» содержит матрицу корреляции между всеми переменными модели, а также строит облако наблюдений для выделенной пары значений.

Облако наблюдений позволяет визуально определить, похожа ли зависимость одной переменной от другой на линейную.

Если среди факторов встречаются сильно коррелирующие между собой, исключите один из них. При желании вместо модели обычной линейной регрессии вы можете построить модель с инструментальными переменными, включив в список инструментальных исключённые из-за корреляции факторы.

Матрица корреляции не имеет смысла для модели нелинейной регрессии, поскольку она показывает только силу линейной зависимости.

Помимо проверки каждого коэффициента модели важно знать, насколько она хороша в целом. Для этого вычисляют статистики, расположенные на панели «Статистические характеристики».

Коэффициент детерминации (R 2 ) – наиболее распространённая статистика для оценки качества модели. R 2 рассчитывается по следующей формуле:

n – число наблюдений;

y_i — значения объясняемой переменной;

— среднее значение объясняемой переменной;

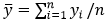
ỹ_i — модельные значения, построенные по оцененным параметрам.

R 2 принимает значение от 0 до 1 и показывает долю объяснённой дисперсии объясняемого ряда. Чем ближе R 2 к 1, тем лучше модель, тем меньше доля необъяснённого.

Возможные проблемы: Проблемы с использованием R 2 заключаются в том, что его значение не уменьшается при добавлении в уравнение факторов, сколь плохи бы они ни были.

где k – число факторов, включенных в модель.

Аналогом t-статистики коэффициента является статистика Фишера (F-статистика). Однако если t-статистика проверяет гипотезу о незначимости одного коэффициента, то F-статистика проверяет гипотезу о том, что все факторы (кроме константы) являются незначимыми. Значение F-статистики также сравнивают с критическим, и для него мы также можем получить вероятность незначимости. Стоит понимать, что данный тест проверяет гипотезу о том, что все факторы одновременно являются незначимыми. Поэтому при наличии незначимых факторов модель в целом может быть значима.

Возможные проблемы: Большинство статистик строится для случая, когда модель включает в себя константу. Однако в Prognoz Platform мы имеем возможность убрать константу из списка оцениваемых коэффициентов. Стоит понимать, что такие манипуляции приводят к тому, что некоторые характеристики могут принимать недопустимые значения. Так, R 2 и Adj R 2 при отсутствии константы могут принимать отрицательные значения. В таком случае их уже не получится интерпретировать как долю, принимающую значение от 0 до 1.

Для моделей без константы в Prognoz Platform рассчитываются нецентрированные коэффициенты детерминации (R 2 и Adj R 2 ). Модифицированная формула приводит их значения к диапазону от 0 до 1 даже в модели без константы.

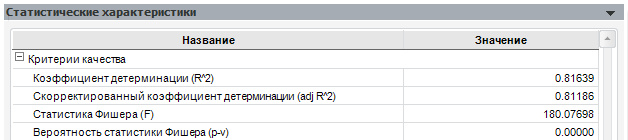
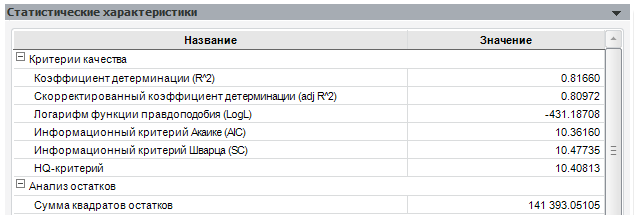
Посмотрим значения описанных критериев для приведённой выше модели:

Как мы видим, коэффициент детерминации достаточно велик, однако есть ещё значительная доля необъяснённой дисперсии. Статистика Фишера говорит о том, что выбранная нами совокупность факторов является значимой.

Кроме критериев, позволяющих говорить о качестве модели самой по себе, существует ряд характеристик, позволяющих сравнивать модели друг с другом (при условии, что мы объясняем один и тот же ряд на одном и том же периоде).

Большинство моделей регрессии сводятся к задаче минимизации суммы квадратов остатков (sum of squared residuals, SSR). Таким образом, сравнивая модели по этому показателю, можно определить, какая из моделей лучше объяснила исследуемый ряд. Такой модели будет соответствовать наименьшее значение суммы квадратов остатков.

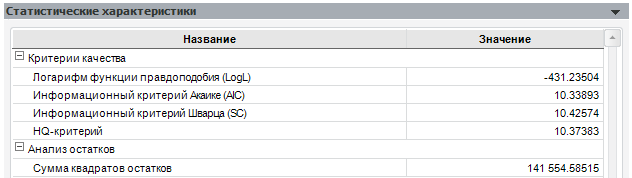
Некоторые модели сводятся к максимизации логарифма функции максимального правдоподобия (LogL). Для модели линейной регрессии эти задачи приводят к одинаковому решению. На основе LogL строятся информационные критерии, часто используемые для решения задачи выбора как регрессионных моделей, так и моделей сглаживания:

Все критерии учитывают число наблюдений и число параметров модели и отличаются друг от друга видом «функции штрафа» за число параметров. Для информационных критериев действует правило: наилучшая модель имеет наименьшее значение критерия.

Сравним нашу модель с её первым вариантом (с «лишним» коэффициентом):

Как можно увидеть, данная модель хоть и дала меньшую сумму квадратов остатков, оказалась хуже по информационным критериям и по скорректированному коэффициенту детерминации.

Модель считается качественной, если остатки модели не коррелируют между собой. В противном случае имеет место постоянное однонаправленное воздействие на объясняемую переменную не учтённых в модели факторов. Это влияет на качество оценок модели, делая их неэффективными.

Для проверки остатков на автокорреляцию первого порядка (зависимость текущего значения от предыдущих) используется статистика Дарбина-Уотсона (DW). Её значение находится в промежутке от 0 до 4. В случае отсутствия автокорреляции DW близка к 2. Близость к 0 говорит о положительной автокорреляции, к 4 — об отрицательной.

Как оказалось, в нашей модели присутствует автокорреляция остатков. От автокорреляции можно избавиться, применив преобразование «Разность» к объясняемой переменной или воспользовавшись другим видом модели – моделью ARIMA или моделью ARMAX.

Возможные проблемы: Статистика Дарбина-Уотсона неприменима к моделям без константы, а также к моделям, которые в качестве факторов используют лагированные значения объясняемой переменной. В этих случаях статистика может показывать отсутствие автокорреляции при её наличии.

Модель линейной регрессии (метод инструментальных переменных)

Модель линейной регрессии с инструментальными переменными имеет вид:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, x̃₁, …, x̃_k – смоделированные при помощи инструментальных переменных объясняющие ряды, z₁, …, z_l – инструментальные переменные, e, ∈_j – вектора ошибок моделей, b₀, b₁, …, b_k – коэффициенты модели, c_0j, c_1j, …, c_lj – коэффициенты моделей для объясняющих рядов.

Схема, по которой следует проверять качество модели, является схожей, только к критериям качества добавляется J-статистика – аналог F-статистики, учитывающий инструментальные переменные.

Модель бинарного выбора

Объясняемой переменной в модели бинарного выбора является величина, принимающая только два значения – 0 или 1.

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели, F – неубывающая функция, возвращающая значения от 0 до 1.

Коэффициенты модели вычисляются методом, максимизирующим значение функции максимального правдоподобия. Для данной модели актуальными будут такие критерии качества, как:

Под моделью линейной регрессии будем понимать модель вида:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b – вектор коэффициентов модели.

Коэффициенты модели вычисляются методом, минимизирующим значение суммы квадратов остатков. Для данной модели будут актуальны те же критерии, что и для линейной регрессии, кроме проверки матрицы корреляций. Отметим ещё, что F-статистика будет проверять, является ли значимой модель в целом по сравнению с моделью y = b₀ + e, даже если в исходной модели у функции f (x₁, …, x_k,b) нет слагаемого, соответствующего константе.

Подведём итоги и представим перечень проверяемых характеристик в виде таблицы:

Надеюсь, данная статья была полезной для читателей!

Источник

К признакам качественной модели не относится

Какая из следующих моделей может быть оценена с помощью МНК 1) y=b0*(x1^b1)*(x2^b2)*e или 2) y=b0*(x1^b1)*(x2^b2)+e?+Первая модель

Какая модель является двойной логарифмической?+LN(Y) = A0 + A1*LN(X1) + LN(E)

Какая модель является линейной?+Y = A0 + A1*X1 + + E

Какая модель является обратной?Y=A0+A1/X1+e

Какая модель является полулогарифмической?Y=A0+A1*LN(X1)+E

Какая неотъемлемая характеристика временного ряда (ВР)+Наличие случайной (шоковой) составляющей

Какая неотъемлемая характеристика системы одновременных уравнений (СОУ)+Набор взаимосвязанных регрессионных моделей, в которых эндогенные переменные в одних моделях являются экзогенными в других

Какая переменная модели квалифицируется как независимая+Экзогенная переменная

Какие из следующих утверждений о свойстве оценок параметров модели в условиях мультиколлинеарности верны+Получение неверных знаков у параметров модели, противоречащих постулатам экономической теории

Какие из следующих утверждений об оценках модели в условиях автокорреляции верны+Оценки дисперсий МНК-оценок параметров оказываются заниженными, что влечет неверные выводы о значимости переменных

Какие оценки дает обычный МНК для уравнений СОУ?+Смещенные и несостоятельные

Какие характеристики обеспечивает взвешенный МНК+Несмещённость оценок в условиях неравноточности проведения наблюдений

Каким образом проверяется наличие пропущенных переменных?+С помощью произведения коэффициентов корреляции пропущенной переменной и остальных переменных модели

Каких переменных не бывает в эконометрических моделяхПостопредельных, корреляционных

Какое значение критерия Дарбина – Вотсона делают позволяет утверждать об отсутствии автокорреляции?DW=2

Какое из следующ. утвержден.о влиянии гетероскедастичности верно+Оценки параметров перестают быть эффективными и состоятельными (ПРАВЕЛЬНЫЙ ВОПРОС)

Какое из следующих утверждений о влиянии (последствиях) гетероскедастичности является неверным?– Оценки параметров модели перестают быть эффективными и состоятельными- Оценки параметров модели остаются несмещенными- Дисперсии оценок параметров рассчитываются со смещением- Выводы полученные на основе t и F статистик, интервальные оценки ненадежны – это все верное

Какое из следующих утверждений о свойстве оценок параметров модели в условиях мультиколллениарности верноПолучение неверных знаков у параметров модели, противоречащих постулатам эконометрической теории

Какое из следующих утверждений об оценках модели в условиях автокорреляции является неверным?Оценки параметров, оставаясь несмещенными, перестают быть эффективными-Дисперсии оценок являются смещенными-Снижение значимости оценок параметров-Выводы по моделям – неверны-Прогнозные качества модели ухудшаются – это все верное

Какое из утверждений верное?+Наблюдаемое значение t-статистики некоторого параметра модели зависит от значения самого параметра и несмещенной дисперсии случайной величины (обратить внимание)

Какое из утверждений неверное применительно к парной регрессии?+Если коэффициент детерминации больше единицы, то все точки лежат ниже прямой регрессии

Какое распределение должны иметь остатки модели?+Нормальное

Какое распределение используется при построении доверительного интервала для параметров модели?+Распределение Стьюдента

Какое распределение используется при построении доверительного интервала для эндогенной переменной модели?+Распределение Стьюдента (обратить внимание)

Какое распределение используется при проверке гипотезы о статистической значимости параметров модели?+Распределение Стьюдента

Какое распределение используется при проверке гипотезы об адекватности регрессионной модели?+Распределение Фишера

Какое уравнение регрессии относится к линейным моделям?Эмпирическое

Какое уравнение регрессии относится к двойной логарифмической модели?LN(Y)=A0+A1*LN(X1)+LN(E)

Какое утверждение неверно для модели Y=2+3*X1-4*X2?

Какой вид уравнений не используется в эконометрических моделях?Предопределенное уравнение

Какой вывод можно сделать, если в модели Рамсея расчетное значение критерия Фишера больше критического?+Модель плохо специфицирована

Какой вывод можно сделать, если критерий Амемья для первой модели больше, чем для второй?+Вторая модель лучше специфицирована

Какой вывод можно сделать, если наблюдаемое значение статистики Дарбина-Вотсона находится между нижней и верхней границей критических значений?+Объем выборки недостаточен для принятия решения

Какой зависимости соответст. структура распределения лагов по Койку+Зависимости по убывающей геометрической прогрессии

Какой из методов не относится к методам диагностики мультиколллениарности?Критерий Дарбина-Вотсона

Какой критерий используется для диагностики автокорреляции?+Дарбина-Вотсона

Какой критерий используется для обнаружения автокорреляции?Используются: 1. Графический метод, 2. Метод рядов, 3. Метод Дарбина-Вотсона

Какой критерий не использ. для диагностики гетероскедастичности?+Дарбина-Вотсона

Какой метод является самым распространенным при оценке параметров регрессионной модели?+Метод наименьших квадратов (МНК)

Какой можно сделать вывод, если для некоторого параметра модели наблюдаемое значение t-статистики равно 4.8, а пороговое значение 2.4?+Рассматриваемый параметр статистически значим

Какой принцип лежит в специфик. модели с помощ. критерия Рамсея?+Построение расширенной модели, в которую включены функция эндогенной переменной, соответствующая распределению остатков первоначальной модели

Какой смысл вкладывается в понятие «адекватности модели»+Соответствие расчетных значений по модели выборочным данным

Коэффициент детерминации это-Это коэффициент значимости параметров модели

На чем основаны методы устранения автокорреляции+На применении оператора декорреляции

Нелинейные модели допускают их сведение к линейным путем процессаЛиниализации

Опасность наличия избыточных переменных заключается вСмещении оценок параметров при включенных переменных

Опасность наличия пропущенных переменных заключается вСмещении оценок параметров при включении в модель переменных

Основная задача регрессионного анализа – этоНахождение случайной переменной и оценивание её параметров

Основная задача эконометрики состоит вСостоит в проверке обоснованности и адекватности модели

Остатки модели должны иметь следующее распределениеНормальное

От чего не зависят табличные значения статистики Дарбина-Уотсона?+От дисперсии экзогенных переменных

Оценки параметров модели множественной регрессии строятся с помощью критерияКритерия Фишера

При каком значении статистика Дарбина – Вотсона делают вывод о наличии положительной автокорреляции в модели?DW=0

При каком значении статистики Дарбина – Вотсона делают вывод об отсутствии в модели автокорреляции 1-го порядка?+DW=2

При нарушении гипотезы о равнозначности измерения эндогенной переменной в различные моменты наблюдения возникает проблемаГетероскедастичности

При обнаружении точной или стахостической линейной взаимосвязи двух или нескольких экзогенных переменных говорят о проблемеМультиколлениарности

При построении доверительного интервала для параметров модели используетсяРаспределение Стьюдента

При построении доверительного интервала для эндогенной переменной модели используетсяРаспределение Фишера

При проверке гипотезы о статистической значимости параметров модели используетсяРаспределение Стьюдента

При проверке гипотезы об адекватности регрессионной модели используетсяРаспределение Фишера

Признаком, по которому определяют пропущенную переменную служитСлужит положительный знак у произведения оценки параметра при подозреваемой переменной на роль пропущенной

Применительно к парной регрессии какое из утверждений неверное?Если коэффициент детерминации больше единицы, то все точки лежат ниже прямой регрессии

Различают мультиколллениарностиЯвную и неявную

С помощью какого критерия проверяется значимость коэффициента детерминации в модели множественной регрессии?+Критерий Фишера

С помощью какого критерия строятся оценки параметров модели множественной регрессии? +Критерий Стьюдента

Чем отличается метод скользящего среднего от метода экспоненциального сглаживания+Взвешиванием уровней ряда, участвующих в сглаживании

Чем отличается модель множественной регрессии от модели парной регрессии?+В модели множественной регрессии более одной экзогенной переменной

Чем отличается структурная форма СОУ от приведенной+Возможностью строить прогнозы для всех эндогенных переменных

Чем является «е» в уравнении простой регреси Y=a*X+b+e?Случайной переменной

Что значит спецификация экзогенных переменных?+Это поиск пропущенных и избыточных переменных

Что не относится к методам диагностики мультиколлинеарности?+Критерий Дарбина-Вотсона

Что не относится к методам сглаживания временных рядов?+Последовательные произведения

Что не относится к методам спецификации эконометрической модели?+Построение оценок параметров модели

Что не относится к последствиям наличия в модели автокорреляции?+Снижение дисперсий оценок параметров модели

Что не является одним из 5 класических предположений МНК?+Наличие корреляции случайных переменных

Что не является признаком наличия мультиколлинеарности?+Возрастание значимости оценок параметров при неколлинеарных экзогенных переменных

Что необходимо для устранения мультиколлинеарности+Все ответы верны

Что означает «мертвая» зона критерия Дарбина – Вотсона?+Недостаточный объем выборки о вынесении решения

Что означает лаг?+Запаздывание при воздействии фактора на эндогенную переменную

Что относится к характеристикам стационарных временных рядов в широком смысле?+Постоянное среднее значение и дисперсия эндогенной переменной

Что происходит при уменьшении доверительной вероятности (гамма) от 0.95 до 0.90?Доверительные интервалы сужаются пороговые значения t-статистик уменьшаются

Что происходит при увеличении доверительной вероятности (гамма) от 0.95 до 0.99?Доверительные интервалы расширяются, пороговые значения t-статистик возрастают?

Что происходит при увеличении уровня надежности (гамма) от 0.90 до 0.95?+Доверительные интервалы расширяются, пороговые значения t-статистик возрастают

Что происходит при уменьшении уровня надежности (гамма) от 0.95 до 0.90?+Доверительные интервалы сужаются пороговые значения t-статистик уменьшаются

Что такое “лаговая переменная”?+Переменная, относящаяся к предыдущим моментам времени

Что такое Y в уравнении простой регрессии Y=a*X+b+e?Эндогенная переменная

Что такое А1 и А2 в уравнении простой регрессии y=A1*X+A2+EПараметры модели?

Что такое автокорреляция?+Точная или стахостическая зависимость между уровнями случайной переменной в различные промежутки времени

Что такое автокорреляция?Статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом

Что такое авторегрессионный процесс?+Процесс, представляющий эндогенную переменную в виде линейной функции предыдущих значений эндогенной переменной

Что такое гетероскедастичность?+Различие дисперсии ошибок в различные моменты времени

Что такое гетероскедастичность?Неоднородность наблюдений, выражающаяся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели

Что такое гомоскедастичность?+Это равенство дисперсий случайной переменной во все моменты времени

Что такое избыточная переменная?+Переменная, которую следует исключить из модели

Что такое коэффициент детерминации?+Значение, показывающее степень адекватности модели

Что такое мультиколлениарность?Точная или стохастическая линейная взаимосвязь двух или нескольких экзогенных переменных

Что такое пропущенная переменная?+Переменная, которую следует добавить в модель

Что такое пропущенная переменная?Фактор который по ошибке небыл включен в эконометрическую модель

Что такое Х в уравнении простой регрессии Y=a*X+b+e?Экзогенная переменная

Что является основными задачами регрессионного анализа?Спецификация модели и оценивание параметров модели

Что является типичным последствием явления гетероскедастичности?+Увеличение дисперсии параметров модели и смещение их оценок

Эконометрические модели подразделяются наПространственные, временные и пространственно-временные

Этап моделирования, на котором осуществляется проверка качества математической модели и точности эконометрических выводов и рекомендаций, называетсяВерификационный

Источник