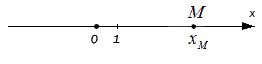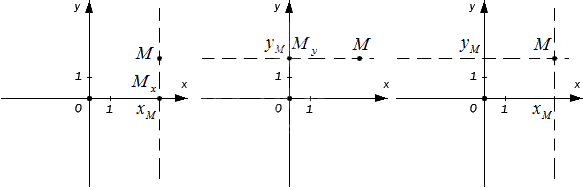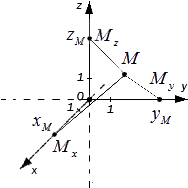За что отвечает ось z
Прямоугольная система координат на плоскости и в пространстве
При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.
Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.
Прямоугольная декартова система координат на плоскости
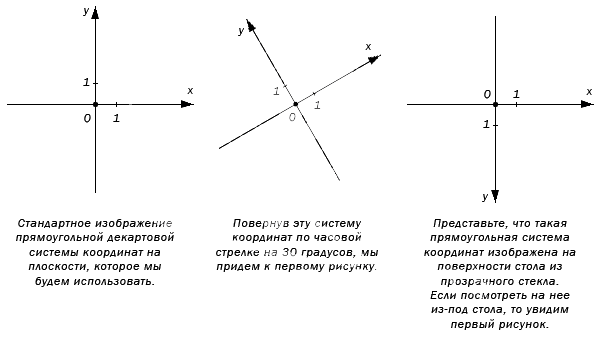
Изображение прямоугольной системы координат на плоскости.
Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.
Прямоугольная система координат в трехмерном пространстве
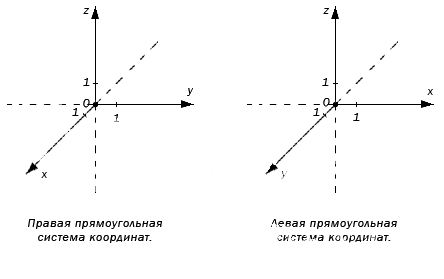
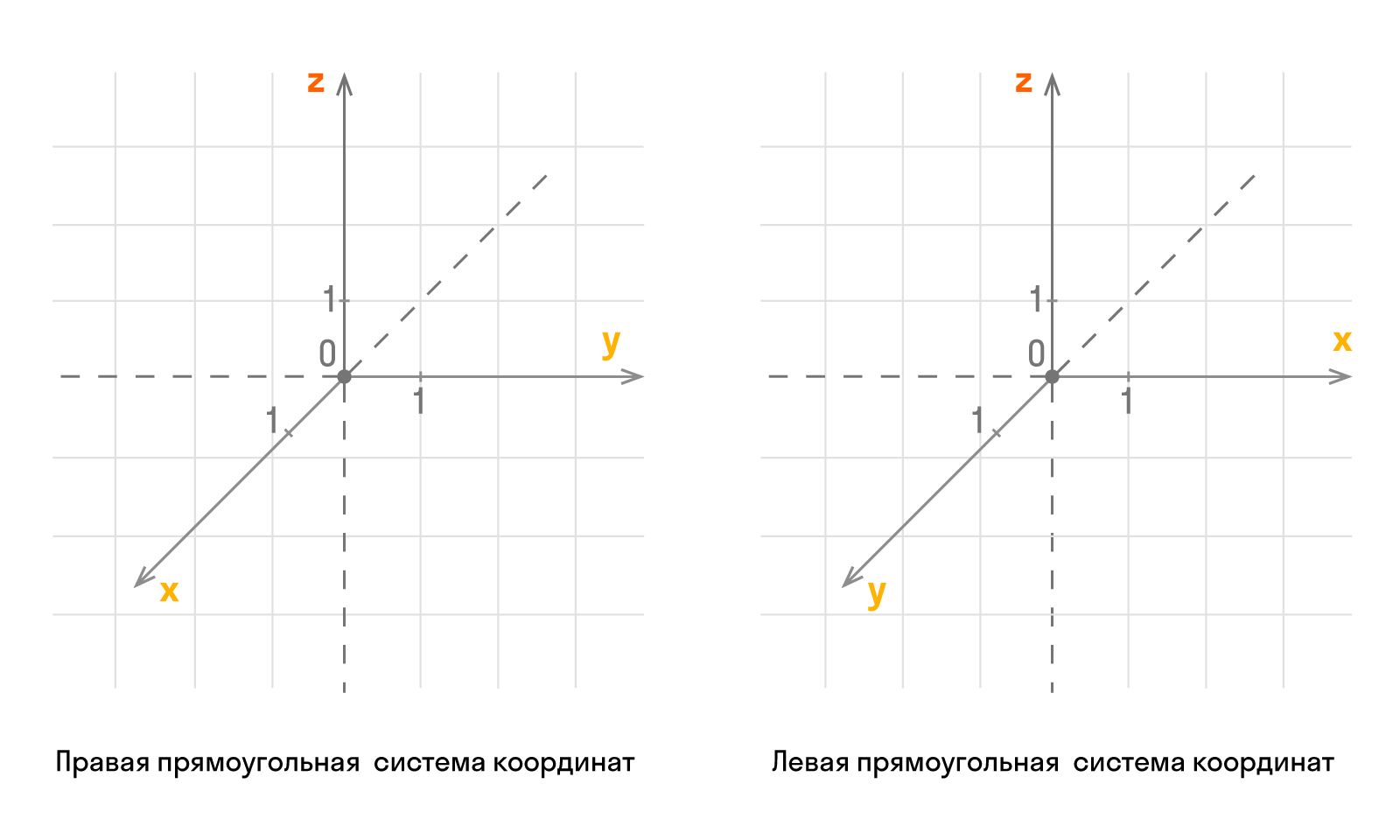
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.
Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат на плоскости
Имеющееся число x M называют координатой точки М на заданной координатной прямой.
Координаты точки в прямоугольной системе координат в трехмерном пространстве
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
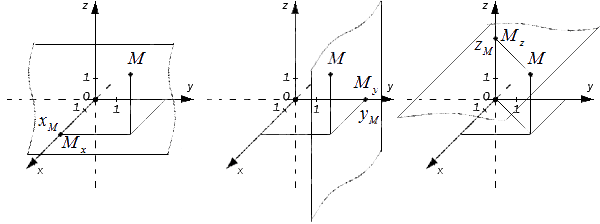
Прямоугольная система координат в трехмерном пространстве
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
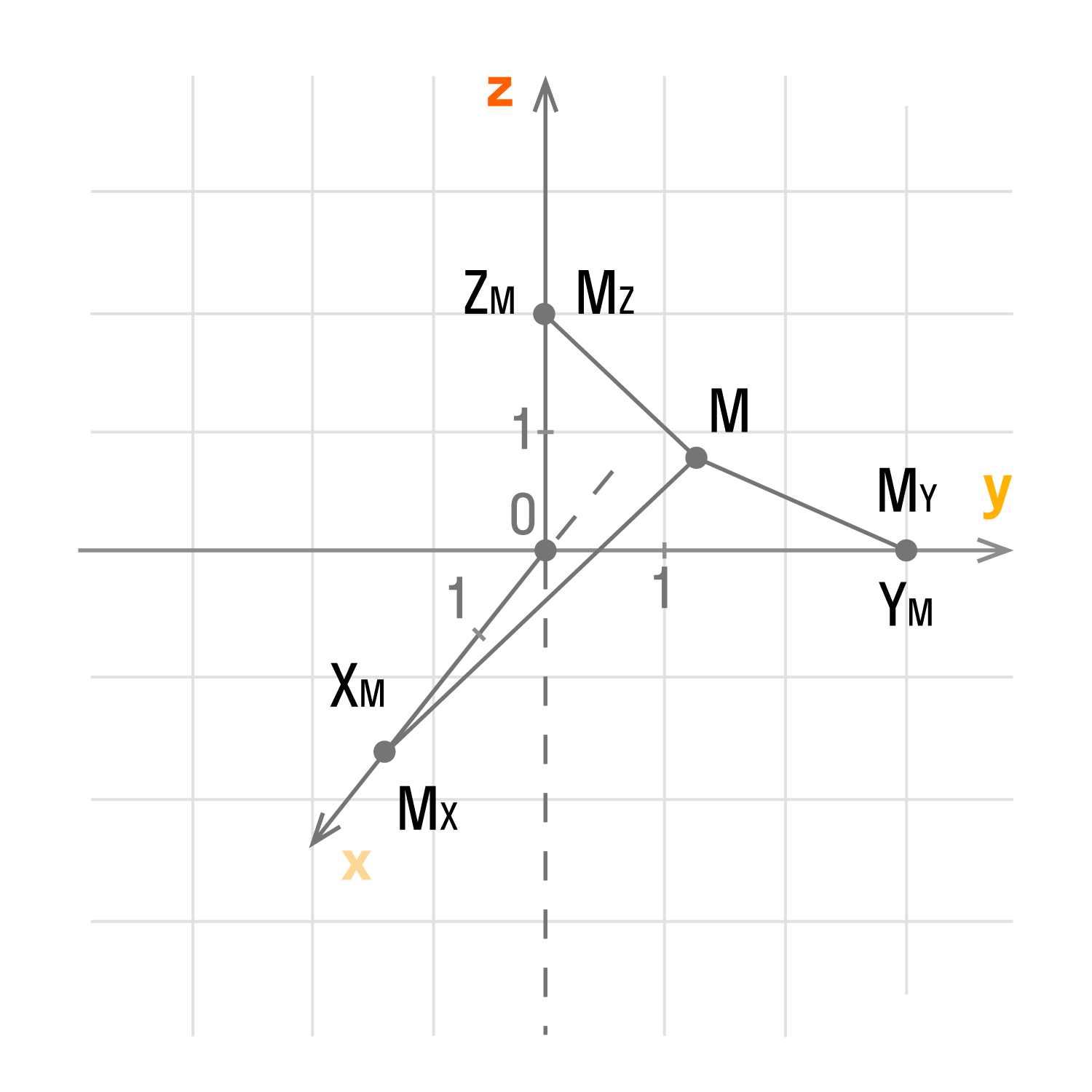
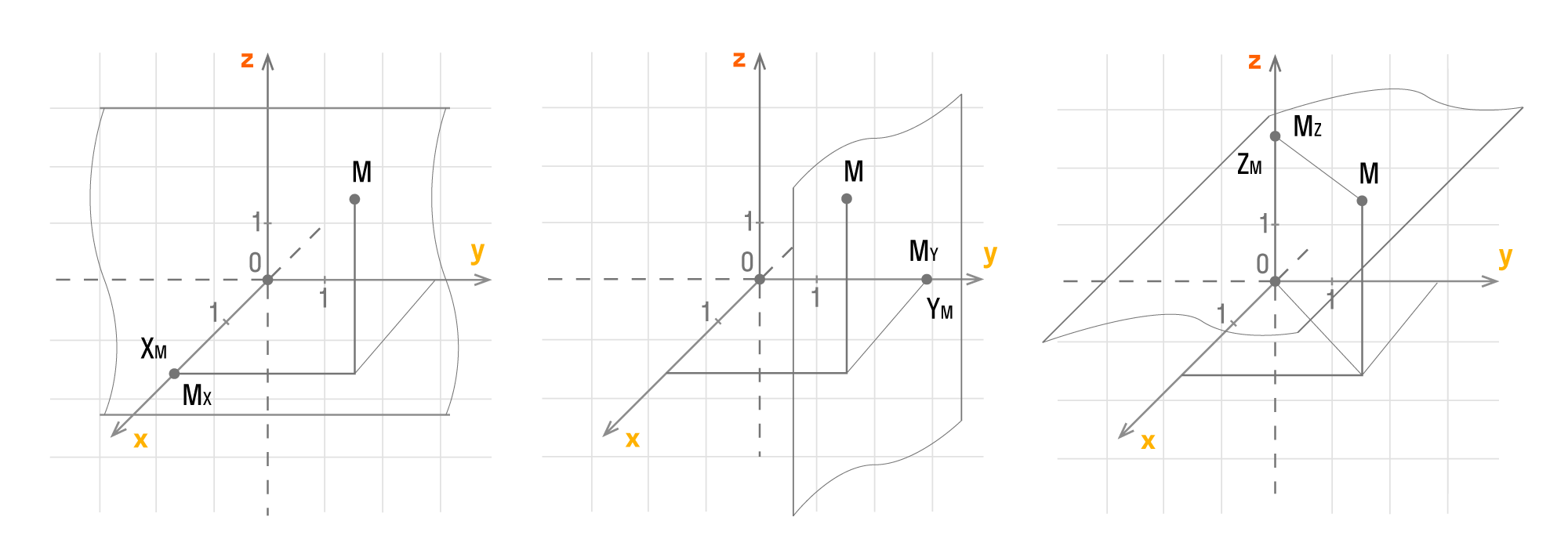
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты точки в трехмерном пространстве
Сформулируем определение точки М в трехмерном пространстве.
Пусть Mx, My, Mz — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения xM, yM, zM. Как это выглядит на координатных прямых:
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в Mx, My, Mz.
У каждой точки трехмерного пространства есть свои данные (xM, yM, zM), которые являются координатами точки М.
xM, yM, zM — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.
Знакомство с осями X, Y, Z
Когда мы работаем в программе для создания 3-D графики, мы имитируем окружающий мир в цифровом форме в трех измерениях. У нас есть направления влево и вправо, вверх и вниз, назад и вперед. Этим трем направлениям соответствуют оси координат X, Y и Z. Мы используем эти оси для измерений и навигации по нашему виртуальному 3-D миру. Эти оси могут использоваться для определения местоположения объектов в системе координат и размера объектов, а также для измерения расстояния между объектами.
Представьте себе город с высокими зданиями. Карта города изображена вдоль двух из этих трех осей. Любой перекресток в городе мог быть описан через два числа координат. Например, мы можем перейти к зданию на углу 3-й и 4-й улиц. Этажи этого здания можно считать третьей осью в нашем 3-D мире. Таким образом, координата (3,4,5) будет означать пятый этаж здания на перекрестке 3-й и 4-й улиц.
Когда мы управляем объектами В 3D приложении, действует та же система измерения. Перемещая объект в 3D пространстве, мы видим, как он двигается по прямой, но само 3D приложение воспринимает это действие как перемещение вдоль осей X, Y, и Z. Аналогично, когда мы изменяем размер объекта на больший или меньший, значения изменений предоставляются в рамках заданной системы координат по осям X, Y, и Z. И когда мы поворачиваем объекты, мы измеряем это как градус вращения, происходящее вокруг этих осей.
Таким образом, наш мир можно изобразить с помощью трехмерной системы координат. Понимание этой системы координат является первым шагом к работе в 3-D.
Едем вниз — растём вверх, или ось Z за недорого
Доброго вам времени суток, уважаемые гики и сочувствующие! Эта публикация — продолжение описания конструкции моего самодельного 3D принтера. Ось Z — один из самых противоречивых узлов принтера. Что выбрать — ультимативную точность или хорошее масштабирование? Перемещать ось Х или рабочий стол принтера? Два подхода — два решения.
На первые 3D принтеры я не мог смотреть без содрогания: конструкции были незрелые, многие узлы использовались с нарушением ТУ, из-за общей зыбкости требовалась постоянная подстройка, мелкий ремонт, размеры рабочего поля были малыми. Я реши решить проблему внутренних противоречий, просто скрестив ежа с ужом конструкции портального фрезерного станка и 3D принтера.
Был спроектирован и скручен воедино остов 3D монстра:
Он состоит из сорокамиллиметровых алюминиевых конструкционных профилей, соединяемых толстыми уголками 45х45 и болтами М8. Эта конструкция имеет размеры 60х40х40 см и абсолютно непоколебима при нормальной работе принтера. Размер рабочей площадки составлял 45х22 см, при максимальной высоте объекта 28 см.
Ось Z образована двумя вертикально расположенными двадцатимиллиметровыми линейными шинами с прецизионными каретками. Каретки приводятся в движение прецизионными трапецевидными винтами, установленными на радиально-упорные подшипники. Каждый винт имеет привод от шагового мотора через ременную передачу 3:1. Верхние концы винтов обточены и вставлены в игольчатые втулки так, чтобы осевое смещение винта во втулке предотвращало его подклинивание при тепловом расширении. Я использовал полимерную гайку для винтов: больших скоростей/нагрузок нет, а полимерная гайка не так требовательна к смазке и значительно проще в монтаже. В данной конструкции рост высоты модели обеспечивается поднятием оси Х над столом, а ось Z используется как подвижная опора для оси X.
Эта ось работала без каких-либо проблем вплоть до разборки этого принтера на запчасти.
Недостатки данного решения:
1. Цена. Прецизионные компоненты стоят дорого.
2. Сложность конструкции
3. Плохая масштабируемость.
Когда я начал строить второй принтер, опыт и скаредность участвовали в создании конструкции наравне с врождённым желанием идти своим путём, не ожидая милостей от природы.
Соответственно, новый принтер должен был стать не только более простым, быстрым, универсальным, надёжным и ремонтопригодным, но и значительно более дешёвым.
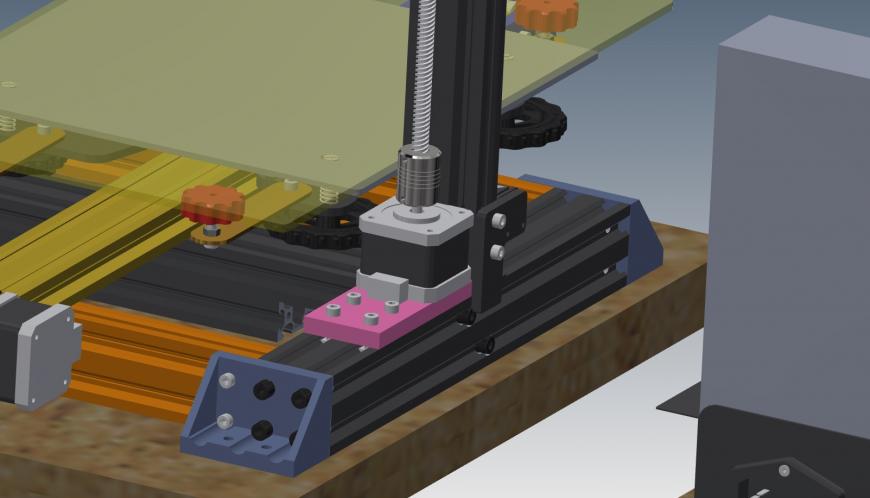
Для оси Z нового принтера был выбран не винтовой привод, а сходная с лебёдкой грузовых кранов тросовая конструкция. Она состоит из собственно приводного механизма с ремённым понижающим редуктором и двух блоков, на которые и ложится вся масса по оси Z.
Здесь фото принтера в целом:
За стабильность пространственной ориентации отвечают две круглые десятимиллиметровые стальные шины, по которым перемещаются парные подшипники скольжения из синтерной бронзы.
На следующих двух видео можно рассмотреть конструкцию лебёдки, там ничего сложного:
Остов оси Z: простая и лёгкая конструкция.
Расчёты по мощности: Приводной барабан имеет радиус 10 мм. Соответственно, крутящий момент 0,3 Нм (обычный мотор Nema 17) на рычаге в 10 мм составит 30 Н. Ременный редуктор с передаточным числом 2:1 удваивает это число.
Вследствие этого максимальное усилие, которое может развить эта лебёдка, составляет около 60 Ньютон, соответственно максимальная масса оси Z вместе с массами стола и объекта не должна превышать 6 кг в покое.
Теперь определим потери на разгон и торможение оси Z: для разгона 1кг массы с ускорением 1 м/с², необходимо приложить силу в 1 Ньютон. На самом деле, ускорения 1 м/с² для оси Z вполне достаточно, и каждый разгоняемый килограмм обойдётся нам в 1 Н приложенной силы.
Самый тяжёлый элемент в конструкции — подогреваемый стол, это дюралюминиевая пластина 350х350х3 мм весом 980 грамм с приклеенными нагревательными элементами общим весом 150 грамм.
Остальные элементы конструкции, включая теплоизоляцию из Basotect, весят около 900 грамм.
Общий вес конструкции составляет около 2030 грамм, что при округлении в большую сторону потребует 21 Н для удержания и ещё 2,1 Н для ускорения. Итого, ещё раз округляя в сторону больших значений, 24 Н.
Если же к массе оси Z добавить килограммовую модель, то понадобится уже 34 Н, что составляет
чуть более половины расчётной мощности лебёдки. Казалось бы, конструкция избыточна по мощности. Но дьявол, как всегда, кроется в деталях. Дело в том, что для достижения максимального крутящего момента через обмотки мотора должны течь максимальные токи, что неизбежно вызовет его перегрев и преждевременный выход из строя.
По этой причине я и спроектировал конструкцию с условием большого запаса по мощности, а ток мотора установил опытным путём чуть больше минимально необходимого. Мотор при этом нагревался до 50-60°С, что вполне допустимо по ТУ.
На этом видео лебёдка легко жонглирует осью Z без рабочего стола, но с двумя катушками филамента весом по 1300 грамм:
Итак, вопрос мощности решён. Теперь поговорим о точности. Учитывая параметры компонентов лебёдки и мотора, при микростеппинге 1/16 возможно перемещение оси Z с шагом 0,02 мм. Теперь рассмотрим проблему точности у лебёдки с однослойной намоткой троса. Радиус приводного барабана в моей конструкции составляет 10 мм, соответственно, длина окружности при намотке будет 62,8 мм. Для того, чтобы поднять ось Z на 44 см, необходимо примерно семь оборотов. При использовании троса толщиной 1 мм осевое смещение намотки составит 7 мм. При этом происходит изменение расстояния от точки соприкосновения троса с барабаном до нижнего опорного блока.
Посчитаем, насколько всё плохо: ведущий барабан находится в центре одной из диагоналей квадрата, образованного нижней частью корпуса принтера. Соответственно, барабан удалён от каждого из нижних опорных блоков на 320 мм. Путём нехитрых расчётов выясняется, что при перемещении стола на 440 мм произойдёт изменение геометрии привода на 0,077 мм.
Качественные винты с трапецевидной резьбой обеспечивают точность от 0,07 до 0,4 мм на таких расстояниях. Проще говоря, не обеспечивают никакого значимого выигрыша по точности. Если же по каким-то причинам Вам необходимо напечатать модели высотой большей, чем 44 см, нужно просто пропорционально увеличить диаметр приводного барабана (для сохранения малого количества оборотов, потребных для перемещения оси) и передаточное число редуктора (для сохранения номинальной нагрузки на мотор). При этом стоимость механизма растёт незначительно, в отличие от конструкции с винтовым приводом.
Один из тестовых объектов:
В заключение могу сказать: хотя опыт и является производной от преодолённых трудностей и совершённых ошибок, но иногда процесс его приобретения доставляет больше удовольствия, чем достигнутые результаты.
3D моделей не будет, ибо я их никак не могу отыскать на диске.
ИНСТРУКЦИЯ Настройка механики ОСИ Z. Creality Ender 3
Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Статья относится к принтерам:
Многие посчитают, что настойка оси Z проста и не нужно заморачиваться, ведь принтер печатает, а значит все хорошо.
Но так будет продолжаться не долго, пока не появятся закусывания оси, спотыкания кареток, разрывы в слоях многочасовой печати, особенно на более массивных и сложных деталях.
Проблема оси Z зависит от:
— перекоса каретки, на которой стоит втулка
— перекоса двигателя оси, а значит и перекоса всего ШВП из-за непродуманного пластикового крепежа.
— несоосность оси Z со втулкой на раме (особенно при перекосе двигателя.)
К сожалению, очень сложно настроить качественно ось Z, со штатным пластиковым крепежом, который из-за своей хлипкости, приводит к перкосам и не позволяет выровнять соосность из-за фиксации в висячем положении в одном есте, нет возможности сдвинуть его в плоскости X иY
И так, как правильно настроить осьZ:
1) Собираем или пересобираем (если новый принтер то по любому) качественно раму и проверяем уголкам перпендикулярность и хорошо закручиваем винты.
2) Настраиваем каретки оси, при этом помним, что на каждой каретке есть шестигранные регулировочные гайки, проворачивая которые, можно поджать или отпустить каретку. Сила поджима должна быть такова, чтобы каретка не болталась, но и не ходила туго, а внутренние колеса каретки под V-slot, должны с небольшим усилием прокручиваться.
4) Обратите внимание на то, что ЛАТУНЕВАЯ втулка на оси снята. Это сделано для того, чтобы выставить мотор и ШВП идеально соосно с отверстием каретки, в котором стоит втулка. После фиксации пластины на раме, приподнимаем каретку оси Z к самому верху, чтобы убедиться, что нет перкоса ШВП и при этом можно провернуть вал и посмотреть, нет ли биения (убедиться, что он не кривой).
5) Дальше вкручиваем втулку, она должна идеально встать на каретке, но на этом настройка не заканчивается.
Нужно открутить трапециевидный винт на штатной муфте (не используйте гибкие разрезные муфты, они только вредят, при этом имеют свободный ход растяжения 5 мм, что может негативно сказываться на печати)
Приподнимаем каретку к самому верху, а вал опускаем к краю муфты.
Такими действиями, мы проверяем параллельность поверхности каретки (на которой установлена втулка) относительно поверхности мотора и рамы.
Если мы видим, что наш вал смещен в одну из сторон больше, относительно отверстия муфты, например ближе к нам, то это значит, что каретка имеет перекос в противоположную сторону.
Чтобы это исправить, нужно приложить немного усилия и руками подогнуть нашу каретку. Она выполнена в виде уголка из достаточно гибкого материал и зачастую не имеет идеальной перпендикулярности, об этом да же есть видео на англоязычном канале. По этому Вы можете ее правильно выставить, это буквально на пару миллиметров, но этого будет достаточно, чтобы получить идеальную соосность с муфтой.
После такой настройки оси Z, движение каретки будет очень легким. Даже без придерживания принтера руками, Вы сможете перемещать каретку вверх или вниз с помощью только двух пальце.
Так же Вы можете посмотреть подробное ВИДЕО о настройке оси: