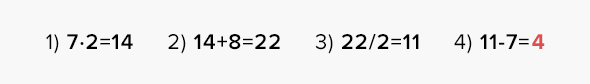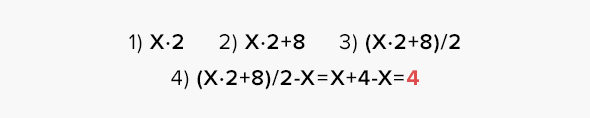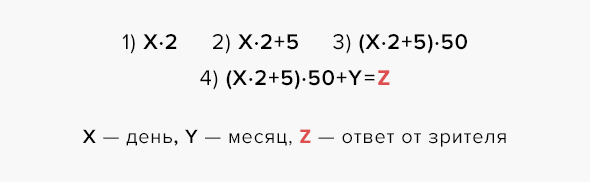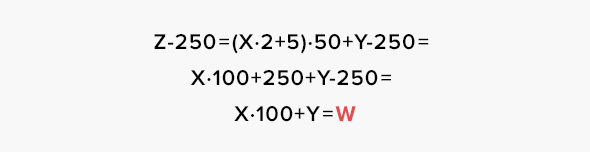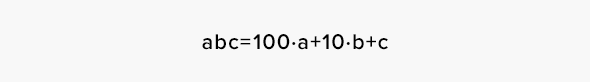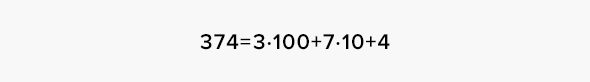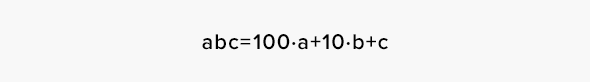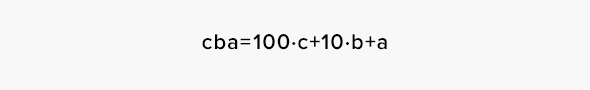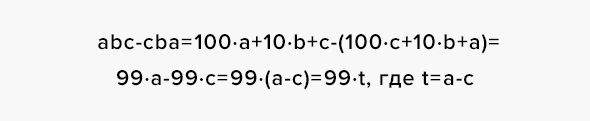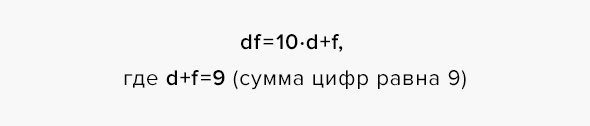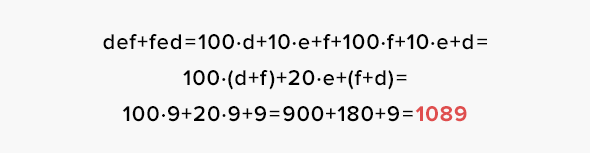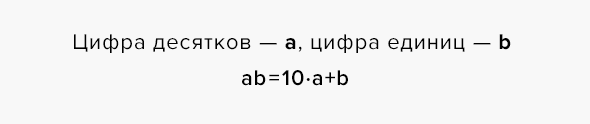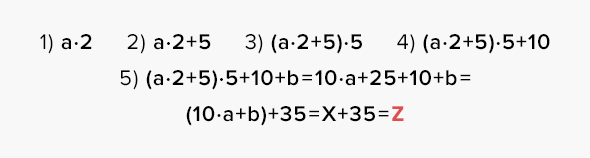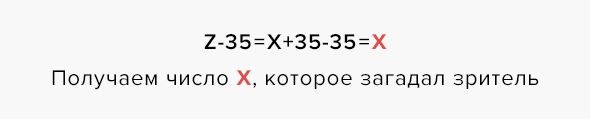Задача скажем что число а скрывает в себе число

1. Скажем, что число А скрывает себе число В, если из А можно вычеркнуть несколько цифр так, чтобы получить В (например, число 123 скрывает в себе числа 1,2,3,12,13 и 23). Найдите наименьшее натуральное число, которое скрывает в себе все числа от 2000 до 2021. Натуральные числа это числа, используемые для счёта предметов.

Ответы 10

Берем наименьшее из чисел 1202

Для получения 1220, необходимо иметь 0 после второй 2 → 12020

Чтобы иметь 2120, необходимо между 2 иметь 1.

01 Удалить ответ +1 балл

а где фот и что надо делать я отличнеца по математеке

Берем наименьшее из чисел 1202

Для получения 1220, необходимо иметь 0 после второй 2 → 12020

Чтоби иметь 2120, необходимо между 2 иметь 1.

01 Удалить ответ +1 балл

Натуральние числа — числа, возникающие естественным образом при счёте (1, 2, 3, 4, 5, 6, 7 и так далее.

Все числа 2021,2120,1220 и 1202 содержат 1, наименьшее из натуральних

Источник

Задача скажем что число а скрывает в себе число

а) Можно ли вычеркнуть несколько цифр из числа 123456789 так, чтобы получилось число, кратное 72?

б) Можно ли вычеркнуть несколько цифр из числа 846927531 так, чтобы получилось число, кратное 72?

в) Какое наибольшее количество цифр можно вычеркнуть из числа 124875963 так, чтобы получилось число, кратное 72?

а) Например, если из числа 123456789 вычеркнуть цифры 2, 7 и 9, то получится число 134568, кратное 72.

б) Предположим, что можно вычеркнуть несколько цифр из числа 846927531 так, чтобы получилось число, кратное 72.

Если число кратно 72, то оно чётное. Значит, цифры 7, 5, 3 и 1 должны быть вычеркнуты. Получается число 84692. Оно не кратно 72, поэтому из него надо вычеркнуть цифры так. чтобы получилось число, кратное 72. Значит, сумма оставшихся цифр должна делиться на 9, то есть сумма вычеркнутых цифр должна быть равна 2, 11 или 20. Это возможно, только если вычеркнуть или 2, или 2 и 9, или 2, 4, 6 и 8. Ни одно из получающихся чисел: 8469, 846. 9 — не делится на 72.

в) Заметим, что все цифры числа 124875963 различны и не равны нулю.

Если вычеркнуть из исходного числа 8 или 7 цифр, то получится число, меньшее 100. Среди таких чисел только 72 делится на 72, но его нельзя получить при вычёркивании цифр из исходного числа.

Если вычеркнуть из исходного числа 6 цифр, то получится трёхзначное число. Среди трёхзначных чисел, все цифры в которых различны и не равны нулю, на 72 делятся только следующие: 216, 432, 576, 648, 792, 864, 936. Ни одно из них нс получается при вычёркивании из числа 124875963 нескольких цифр.

Значит, нельзя вычеркнуть более 5 цифр так, чтобы получившееся число было кратно 72. Пять цифр вычеркнуть можно. Например, если вычеркнуть цифры 4, 8. 7, 5 и 3. то получится число 1296, кратное 72.

Источник

Из числа А вычесть число В.

Если получилось отрицательное значение, то сообщить, что число В больше.

Если получилось положительное значение, то сообщить, что число А больше.

При всей простоте и очевидности алгоритма, не каждый сразу поймет его ошибочность. Ведь если оба числа равны, то не получится никакого сообщения. Значит, надо обязательно предусмотреть это вариант, например:

Из числа А вычесть число В.

Если получилось отрицательное значение, то сообщить, что число В больше.

Если получилось положительное значение, то сообщить, что число А больше.

Если получился ноль, то сообщить, что числа равны.

Массовость– один и тот же алгоритм можно использовать с разными исходными данными.

Например: алгоритм приготовления любого бутерброда.

Отрезать ломтик хлеба.

Намазать его маслом.

Отрезать кусок любого другого пищевого продукта (колбасы, сыра, мяса).

Наложить отрезанный кусок на ломоть хлеба.

Возможность автоматизации деятельности человека.

Выполняя алгоритм, исполнитель может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В таком случае говорят, что исполнитель действует формально (механически), т. е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции.

Построение алгоритма для решения задачи из какой-либо области требует от человека глубоких знаний в этой области, бывает связано с тщательным анализом поставленной задачи, сложными, иногда очень громоздкими рассуждениями. На поиски алгоритма решения некоторых задач ученые затрачивают многие годы. Но когда алгоритм создан, решение задачи по готовому алгоритму уже не требует каких-либо рассуждений и сводится только к строгому выполнению команд алгоритма.

В этом случае исполнение алгоритма можно поручить не человеку, а машине. Действительно, простейшие операции, на которые при создании алгоритма расчленяется процесс решения задачи, может реализовать и машина, специально созданная для выполнения отдельных команд алгоритма и выполняющая их в последовательности, указанной в алгоритме. Это положение и лежит в основе работы автоматических устройств, автоматизации деятельности человека.

Способы описания алгоритмов

Словесный (для записи используются специальные формальные языки с ограниченным набором слов и строгими правилами записи. Представляет собой описание последовательных этапов обработки данных), Формульный, Словесно-формульный, Графический(изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий – Блок-схемы).

Блок-схемы позволяют описать алгоритм с использованием минимального количества слов и независимо от выбранного процедурного языка. Порядок действий указывается с помощью стрелок.

Источник

5 простых математических фокусов

Привить любовь к математике можно разными способами, и самый необычный из них — через фокусы. Для некоторых детей этот способ может стать самым действенным — появится реальный стимул тренироваться в устном счёте и разбираться в формулах. Сайт «Фокусы. Как научиться» собрал пять самых интересных математических фокусов, а «Мел» попросил учителя математики Дмитрия Коробченко объяснить, как они работают.

Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках алгебры и геометрии.

И хотя вместо цифр, геометрических фигур в некоторых фокусах мы будем использовать различные предметы, все они связаны с числами. Вначале попробуйте проделать самые простые фокусы. Только помните: эти фокусы с цифрами будут получаться только тогда, когда вы научитесь быстро считать в уме (а вот, кстати, несколько советов, как этому научиться). Поэтому начинать советуем с тренировки в устном счёте, причём от меньших цифр к большим.

Обобщить секрет всех подобных математических фокусов можно следующим образом: зритель загадывает некое случайное число (или числа). Затем мы предлагаем зрителю произвести с этим числом некоторые простые арифметические операции. В итоге у зрителя получается некий финальный результат («ответ»), и наша задача — либо (1) угадать этот результат, либо (2) по этому результату, который зритель нам сообщает, предсказать исходное загаданное число.

1. Угадай число

Содержание фокуса. Попросите любого зрителя задумать число. Потом это число зритель должен умножить на 2, прибавить к результату 8, разделить результат на 2 и задуманное число отнять. В результате вы смело называете число 4.

Пример. Зритель задумал число 7.

Фокус относится к случаю (1). Загадано число X. Зритель выполняет следующие операции:

Мы получили 4 независимо от изначально загаданного числа.

2. Угаданный день рождения

Содержание фокуса. Объявите зрителям, что вы сможете угадать день рождения любого незнакомого человека, сидящего в зале. Вызовите любого желающего и предложите ему умножить на 2 число дня своего рождения. Затем пусть зритель сложит получившееся произведение и число 5 и умножит на 50 полученную сумму. К этому результату необходимо прибавить номер месяца рождения (июль — 7, январь — 1), вслух назвать полученное число. Через секунду вы называете день и месяц рождения зрителя.

Секрет. Все очень просто. В уме от того числа, которое назвал зритель, отнимите 250. У вас должно выйти трехзначное или четырехзначное число. Первая и вторая цифры — день рождения, две последние — месяц.

Фокус относится к случаю (2). Загадан день рождения. День — X, месяц — Y. Оба числа являются не более чем двузначными. Зритель выполняет следующие операции:

В уме отнимаем 250:

Так как Y — не более чем двузначное число, в получившемся числе [W=X*100+Y] месяц Y и день X никак не перемешаются. Поэтому последние две цифры числа W — это месяц Y, остальные — день X.

3. Разгаданный результат математических вычислений

Вам понадобятся: заранее приготовленные листы бумаги, карандаши или ручки, калькуляторы.

Содержание фокуса. Предложите зрителям задумать трехзначное число и записать его на бумаге. При загадывании числа должно быть выполнено одно условие: цифра сотен не должна быть равна цифре единиц и не должна быть на единицу меньше или больше неё. Если вы ещё путаетесь в сотнях и единицах, то на первом месте в трехзначных числах стоят сотни, на втором десятки, на третьем единицы (например, подойдёт число 531).

Пример. Допустим, это и есть число 531. Теперь зрители должны перевернуть задуманное число, то есть написать цифры в обратном порядке (135). Затем зрители должны взять эти два числа и из большего вычесть меньшее (531 — 135). Получившуюся разницу снова нужно перевернуть (396; 693) и сложить эти два числа (396 + 693). Потом один из зрителей должен прибавить к полученной сумме 100, второй — 200, третий — 300 и так далее. Теперь вы можете отгадать, что получилось у каждого зрителя, но при том условии, что они к своему последнему числу прибавят цифру 1 089. У первого зрителя, прибавлявшего 100, получится 1 189, у второго — 1 289, у третьего — 1 389.

Секрет фокуса. Для того чтобы узнать, что получилось, вам не нужно знать задуманное число. Главное — прибавлять к числу 1 089 то число (100, 200, 300, 400…), которое прибавлялось в самом конце. Для того чтобы не перепутать, у кого что получилось, в самом конце фокуса можно раздать карточки с цифрами 100, 200, 300 и попросить держать их при отгадывании конечного результата.

Примечание: Порой в фокусах встречаются различные операции над цифрами, которые входят в состав используемых чисел. В таком случае полезно пользоваться тем фактом, что число с цифрами a, b,c, записанное как «abc», представимо в виде:

Фокус относится к случаю (1). Загадано трёхзначное число, X, записанное как «abc». Цифра сотен — a. Цифра десятков — b. Цифра единиц — c. То есть:

Зритель выполняет следующие операции. Перевернуть число:

Вычесть из большего числа меньшее (допустим, a > c, в противном случае всё будет так же, просто a и c поменяются ролями):

Для дальнейшего действия нам необходимо представить число («abc» — «cba») как «def», то есть найти его сотни, десятки и единицы.

Все такие двузначные числа можно найти в таблице умножения (18, 27, 36, 45, 54, 63, 72, 81), и они обладают следующим свойством: сумма цифр такого числа равна 9. Запишем 9*t как «df»:

Вернёмся к числу «abc» — «cba»:

Дальнейшее действие — получившееся число снова перевернуть и сложить с предыдущим:

В результате мы получили число 1089 независимо от изначально загаданного числа. Далее к этому числу мы просим прибавить 100, 200 или 300 и получаем соответственно 1189, 1289 или 1389.

Ответ: 1189, 1289 или 1389 (в зависимости от зрителя).

4. Угадываем задуманное число

Вам понадобятся: заранее приготовленные листы бумаги (по числу зрителей), карандаши или ручки, калькуляторы.

Содержание фокуса. Предложите зрителям задумать двузначное число. Теперь пусть они умножат число его десятков на 2, прибавят к этому произведению число 5, умножат эту сумму на 5, к полученному произведению прибавят 10 и число единиц того числа, которое задумали. Пусть любой зритель скажет, что у него получилось. Вычтите из полученного результата число 35 (лучше сделать это в уме или на калькуляторе, не посвящая в свои действия зрителей), и вы сможете назвать задуманное зрителями число.

Пример. Все основано на математических закономерностях, о которых вашим зрителям знать необязательно. Как это выглядит в реальном фокусе? Например, зритель задумал число 38: 3 десятка и 8 единиц. Умножаем 3 на 2, получается 6. Прибавляем к 6 число 5, получаем 11. Умножаем эту сумму на 5, получаем 55. Прибавляем 10 и получаем 65. Прибавляем число единиц (8) задуманного числа. Получаем 73, вычитаем 35. В итоге задуманное число — 38.

Фокус относится к случаю (2). Загадано двузначное число X, записанное как «ab»:

Зритель выполняет следующие операции:

Ответ от зрителя — Z. В уме отнимаем 35:

5. Фокус с отгадыванием чисел

Вам понадобятся: заранее приготовленные листы бумаги (по числу зрителей), карандаши или ручки (по числу зрителей), калькуляторы.

Содержание фокуса. Попросите зрителей задумать какое-нибудь число. Вопрос вы можете задать абсолютно любой, например: сколько дней в неделю вы хотели бы кататься на велосипеде, есть манную кашу, не ходить в школу, бегать по лужам. Весь смысл не в вопросе, а в задуманном зрителями числе. Раздайте зрителям бумажки и ручки и попросите письменно ответить на ваш вопрос. Пусть каждый напишет, сколько дней в неделю он хотел бы есть морковку.

Теперь пусть каждый умножит это число на 2, затем к полученному числу морковок прибавит 5, после чего умножит эту сумму на 50. Теперь пусть каждый сделает следующее: если в этом году уже был день рождения, прибавить 1 750, если нет — 1 749. Теперь из этого числа каждый должен вычесть свой год рождения и к этому числу прибавить 7.

Теперь попросите любого из зрителей назвать получившуюся цифру. Должно получиться двузначное или трёхзначное число. Первая цифра — количество морковок, остальные — возраст человека.

Секрет. Секрет фокуса в тех числах, которые вы заставляете их прибавлять, отнимать, делить.

Пример. Допустим, вы загадали 2 дня в неделю для поедания морковки. Теперь умножьте 2 на 2, получится 4. Потом к 4 прибавьте 5, получится 9, затем 9 умножьте на 50, получится 450. Допустим, ваш день рождения 18 июля 1997 года. Например, сейчас сентябрь и ваш день рождения уже прошёл. Значит, прибавьте к 450 число 1 750, получится 2 200. Теперь из числа 2 200 вычтите год рождения 1997, получится 203, к этому числу прибавьте 7. Результат — 210 (2 дня и 10 лет).

Во втором случае из числа 2 199 вычтите 1 997, получится число 202, прибавьте 7, получится 209. Значит, загадано 2 дня морковки и 9 лет загадавшему.

Совет. Перед выполнением этого математического фокуса раздайте зрителям калькуляторы, чтобы они не ошиблись в вычислениях, а для себя на первое время запишите на карточке порядок действий с цифрами: на что умножить, что прибавить, из чего вычесть.

Фокус относится к случаю (2). Но этот фокус работает только в 2007 году. Для других годов нужно заменить число 1750 на другое.

Загадано число морковок X и возраст зрителя Y. Также в задаче участвуют:

Источник

Задача Танежи или проблема числа 10958…

В работе Индера Танежа (Inder J. Taneja) (бразильского математика-популяризатора математики) от 2014 года: Crazy Sequential Representation: Numbers from 0 to 11111 in terms of Increasing and Decreasing Orders of 1 to 9 (Сумасшедшее последовательное представление: числа от 0 до 11111 в порядке возрастания и убывания от 1 до 9).
Был один пробел, а именно число 10958, который немного всколыхнул научное сообщество, и самое главное до сих пор не заполнен. Вот про него мы и поговорим.

Введение

Для начала о самой статье Crazy Sequential Representation… В ней основная часть отведена таблице на 160 листов на которых любое число (от 0 до 11 111) представлено операциями над двумя последовательностями чисел. Последовательности такие:
* 1, 2, 3, 4, 5, 6, 7, 8, 9
* 9, 8, 7, 6, 5, 4, 3, 2, 1
Например, 2021 представить можно так
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
* 2021 = (9×8 + 7 + 6)×5×4 + 321
А 307 так:
* 307 = 123 + 45 + 67 + 8×9
* 307 = 9×8 + 7×6×5 + 4×3×2 + 1
Важно понимать, что последовательности 1, 2…8, 9 и 9, 8…2, 1 не должны нарушаться при визуальной записи. Более того, набор допустимых операций – это самый базовый «школьный» набор:
* plus (плюс);
* minus (минус);
* product (умножение);
* potentiation (возведение в степень);
* division (деление);
* brackets (скобки)

«Сложные» операции такие как — факториал, квадратный корень и т.д. недопустимы…
Самое удивительное, что все числа, до 11 111, мы можем получить благодаря этим базовым операциям… Ну или почти все… Одно число раскололо математическое сообщество на два лагеря. Это число — 10958. В статье Танежа написано так:
* 10958 = still not available (все еще недоступно)
* 10958= (9 + 8 × 7 × 65 + 4) × 3 − 2 + 1

Т.е. математики сначала загнали себе в рамки, а потом раскололись из-за рамок на два лагеря. Первые сказали — что такая последовательность базовых операций должна существовать, но еще не найдена. Вторые – нашли решение, но схитрили и расширили понятие «базовые операции».

О чем спор

Что бы понять «о чем спор» для начала вернемся к числу 2021 из таблицы. Сейчас это число вычисляется так:
* 2021 = 12×(3×4 + 5 + 6)×7 + 89
Как видно, здесь есть два «странных» числа – это 12 и 89, которые выбиваются из начальных условий. Ибо, из «условий задачи», начальные числа должны быть из следующего множества: 1, 2, 3, 4, 5, 6, 7, 8, 9, а тут появляются 12 и 89… Что не совсем честно… И отсюда и появляется идея у одной из групп математиков. Они ввели новую операцию – «конкатенацию» и сказали, что она «базовая»… Проблема в том, что для операции «конкатенации» даже общепринятого символа нет, а тут её решили причислить к базовым…
И раз никто не знает, как её толком обозначить, а мне статью писать нужно, в дальнейшем, операцию «конкатенации» будем обозначать символом ‖ (т.к. именно это обозначение я встречал чаще всего).
Давайте вспомним свойства конкатенации.
1) Операция конкатенации ассоциативна.
То есть, если нужно выполнить конкатенацию трёх слов, то от расстановки скобок результат не изменится: ( wiki ‖ media ) ‖ pedia = wikimediapedia, и в то же время wiki ‖ ( media ‖ pedia ) = wikimediapedia.
2) Операция конкатенации некоммутативна.
В самом деле, wiki ‖ media = wikimedia, но media ‖ wiki = mediawiki ≠ wikimedia. От перестановки операндов меняется результат операции, что и означает её некоммутативность.
3) Пустое слово — ε, — является нейтральным элементом (единицей) операции конкатенации.
То есть, если ε— пустое слово, то для любого слова α выполнено равенство: ε ‖ a = a ‖ ε = a
4) Длина (количество букв) конкатенации слов равна сумме длин операндов:
|α ‖ β| = |α| + |β|.

Эти свойства вполне себе известны и описаны на википедии.
Добавим еще описание приоритетности:
5) (плюс, минус)

Источник