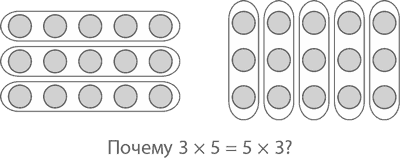
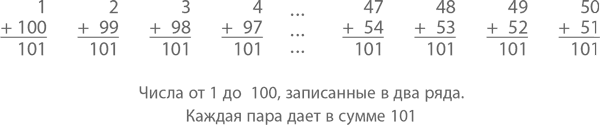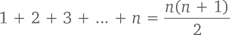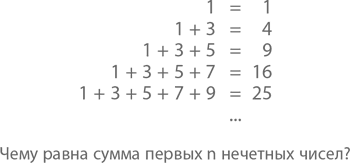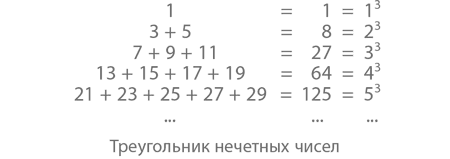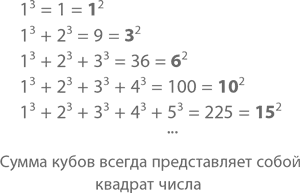Закономерность это что в математике

Числовые закономерности

Изучение математики всегда начинается с чисел. Сначала мы учимся выражать количество с помощью букв, цифр или самих предметов. А потом долгие и долгие годы складываем, вычитаем, умножаем, делим и решаем разные арифметические задачи. И за всей этой рутиной часто не видим магию чисел, способную развлечь и удивить любого, кто решится всего лишь заглянуть чуть глубже.

Вот, например, одна хитрость, с которой еще в детстве столкнулся немецкий математик Карл Фридрих Гаусс[2]. Как-то раз на уроке математики учитель попросил класс сложить между собой всей числа от 1 до 100. Вряд ли он хотел развлечь учеников – скорее, отвлечь: заставить заняться чем-нибудь нудным и требующим полного сосредоточения, а самому спокойно сделать другую работу. Представьте себе его удивление, когда через несколько секунд Гаусс вышел к доске и написал ответ – 5050. Хотите знать, как он это сделал? Он просто представил все эти числа в виде двух рядов: верхний – от 1 до 50, нижний – от 51 до 100, причем в нижнем ряду числа шли в обратном порядке, вот так:

Гаусс заметил, что сумма чисел в каждом из 50 столбцов одинаковая – 101, а значит, для того, чтобы получить искомый результат, нужно всего лишь умножить 101 на 50. Так у него и получилось 5050.

Собственно говоря, благодаря такой вот способности – не быстро считать в уме, но заставлять числа плясать под свою дудку – Гаусс и стал одним из величайших математиков XIX столетия. В этой главе мы как раз и поговорим об интересных числовых закономерностях и, конечно, увидим танец чисел. Одни из этих примеров полезны тем, что развивают способности умственного счета, другие – просто красивы.

Только что мы последовали путем гауссовой логики, чтобы получить сумму первой сотни простых чисел. Но что, если нам нужна сумма 17 из них? Или тысячи? Миллиона? Логика Гаусса позволяет подсчитывать сумму первых n чисел, где n – любое нужное вам количество! Некоторым людям легче разобраться с математическими абстракциями, если они могут их визуализировать. К примеру, числа 1, 3, 6, 10 и 15 иногда называют треугольными, потому что, заменив их соответствующим количеством кружков, можно легко сложить треугольники, вроде того, что изображен чуть ниже (конечно, один кружок треугольником можно назвать с очень большой натяжкой, но число 1, несмотря на это, все же считается треугольным). Согласно определению, треугольное число n равняется 1 + 2 + 3 +… + n.

Посмотрите, что произойдет, если мы расположим два треугольника основаниями друг к другу, вот так:

Видите, закономерность, которую мы использовали для сложения первой сотни чисел, вполне применима к любому подобному ряду, сколько бы членов в него ни входило. И если вдруг нам понадобится сложить между собой все числа от 1 до 1 000 000, сделать это можно будет всего за два шага: перемножив 1 000 000 и 1 000 001 и разделив результат пополам.

Разобравшись в одной формуле, вы с легкостью разберетесь и в остальных. Например, если мы удвоим обе части последнего уравнения, получится формула суммы первых n четных чисел:

2 + 4 + 6 +… + 2n = n(n + 1)

А как насчет суммы первых нечетных, спр?сите вы? Давайте посмотрим, что говорят нам числа.

1 + 3 + 5 + 7 + 9 = 25

И возьми мы квадрат со сторонами n на n, его можно будет легко разбить на n-ное количество L-образных секторов, в каждом из которых будет соответственно 1, 3, 5…., (2n – 1) кружков. Это и есть формула суммы первых n нечетных чисел

1 + 3 + 5 + … + (2n – 1) = n?

Отступление

Эта закономерность может привести нас к другой, еще более красивой. Раз уж мы хотим заставить числа танцевать, почему бы не сделать это и с их квадратами?

Взгляните вот на такую пирамидку уравнений:

Какую закономерность вы видите? Подсчитать количество чисел в каждом ряду несложно: 3, 5, 7, 9, 11 и так далее. А дальше неожиданность: первое число каждого ряда – по крайней мере, первых 5 записанных здесь рядов – является квадратом числа. И правда: 1, 4, 9, 16, 25… Почему так получается? Возьмем пятый ряд. Сколько чисел ему предшествуют? Давайте сложим их количество: 3 + 5 + 7 + 9. Прибавим к ним еще единицу, и у нас получится первое число пятого ряда – сумма первых 5 нечетных чисел, которая, как мы уже знаем, равна 5?.

А теперь просчитаем пятое уравнение, ничего к нему не добавляя. Как бы это сделал Гаусс? Если пока не обращать внимания на начальное 25, слева у нас останется 5 чисел, каждое из которых будет ровно на 5 меньше, чем соответствующее ему число справа.

То есть сумма чисел справа будет ровно на 25 больше суммы чисел слева. Но это без учета 25, которые стоят в начале. А с ними у нас получается именно тот результат, который обещан нам знаком равенства. Следуя той же логике и призвав на помощь алгебру, мы докажем, что этот ряд можно продолжать бесконечно.

Отступление

Перейдем к другой закономерности. Как мы уже видели, из нечетных чисел можно составлять квадраты. А теперь посмотрим, что произойдет, если собрать их в один большой треугольник – вроде того, что изображен чуть ниже.

Так отлично видно, что 3 + 5 = 8, а 7 + 9 + 11 = 27, а 13 + 15 + 17 + 19 = 64. Что общего у 1, 8, 27 и 64? Да это же полные кубы чисел! Например, если сложить между собой пять чисел пятого ряда, мы получим:

Логика вроде бы подсказывает, что сумма чисел в ряду n будет равна n?. Но насколько верным будет этот вывод? Не простое ли это совпадение? Чтобы лучше понять эту закономерность, посмотрим на числа в середине 1, 3 и 5 рядов. Что мы видим? 1, 9 и 25. То есть квадраты. В середине 2 и 4 рядов чисел нет, но по сторонам центра 2 ряда видим числа 3 и 5, среднее арифметическое которых – 4, а по сторонам центра 4 ряда – 15 и 17 со средним арифметическим 16. Давайте подумаем, как эту закономерность можно использовать.

Кстати, если уж мы взялись оперировать квадратами и кубами, не могу удержаться, чтобы не указать вам на еще одну закономерность. Что получится, если сложить кубы чисел, начиная с 1??

Подсчитывая сумму кубов, мы получаем 1, 9, 36, 100, 225 и т. д. – числа, которые являются полными квадратами. Но это не любые квадраты, а квадраты 1, 3, 6, 10, 15 и т. д. – треугольных чисел! Мы уже знаем, что они по своей сути являются суммами простых чисел, а значит,

1? + 2? + 3? + 4? + 5? = 225 = 15? = (1 + 2 + 3 + 4 + 5)?

Другими словами, сумма кубов первых n чисел есть квадрат суммы этих самых первых n чисел. Подтвердить это мы пока не можем, но в главе 6 пару доказательств увидим.

Данный текст является ознакомительным фрагментом.

Источник

Математики нашли закономерность, разбираясь в том, как избежать её появления

Мы, наконец, узнали, насколько большим должно быть множество чисел, чтобы в нём гарантировано содержалась закономерность под названием «многочленная прогрессия»

Некоторые закономерности в математике настолько редкие, что их можно искать всю жизнь и не найти. Другие же встречаются так часто, что их, кажется, невозможно избежать.

Новое доказательство, представленное Сарой Пилюс из Оксфордского университета, показывает, что одна численная закономерность особенно важного типа, по сути, является неизбежной: она гарантированно обнаружится в любой достаточно большой коллекции чисел, вне зависимости от того, как их выбирают.

«Этим закономерностям присуща своего рода неразрушимость», — сказал Теренс Тао из Калифорнийского университета в Лос-Анджелесе.

Доказательство Пилюс касается последовательности чисел под названием «многочленные прогрессии». Их легко создавать – вы очень быстро сможете составить свою – и они касаются связи между сложением и умножением чисел.

Несколько десятилетий математики знали, что при малом размере набора (или «множества») чисел – то есть, когда в нём содержится относительно немного чисел – в нём может вообще не оказаться никаких многочленных прогрессий. Им также было известно, что при росте множества оно в конце концов переходит определённый порог, после которого в нём уже содержится так много чисел, что одна из таких последовательностей обязана там встретиться. Это похоже на миску супа с буковками из теста – чем больше у вас букв, тем больше вероятность, что из них можно складывать слова.

Но до работы Пилюс математики не знали, каков этот порог. Её доказательство даёт ответ на этот вопрос – точную формулу, определяющую, насколько большим должно быть множество, чтобы в нём гарантированно содержались определённые многочленные прогрессии.

А до этого у математиков были только смутные представления о том, что многочленные прогрессии встречаются среди целых чисел (1, 2, 3, и т.п.). Теперь они точно знают, где их искать.

В поисках закономерностей

Чтобы представить себе эти закономерности, рассмотрим одну из них, немного более простую, чем та, с которой работала Пилюс. Начнём с цифры 2 и будем добавлять тройку: 2, 5, 8, 11, 14, и т.д. Такая закономерность – начав с одного номера, добавляем другой – называется «арифметической прогрессией». Это одна из наиболее изученных и частых прогрессий в математике.

Касательно частоты появления арифметической прогрессии среди целых чисел нужно понять две вещи.

Одну из них доказал Эндре Семереди в 1975 году. Сначала, сказал он, выберите длину своей арифметической прогрессии. Это может быть закономерность с четырьмя членами (2, 5, 8, 11), или семью (14, 17, 20, 23, 26, 29, 32), или вообще с любым количеством. После этого он доказывает, что как только множество чисел достигает определённого размера (который он не смог определить), в нём обязательно найдётся арифметическая прогрессия такой длины. Таким образом он укрепил идею о том, что в достаточно больших множествах чисел где-то обязательно найдётся закономерность.

«Семереди, по сути, сказал, что полный беспорядок невозможен. Какое бы множество вы ни взяли, в него всегда сумеет затесаться какая-нибудь структура», — сказал Бен Грин из Оксфорда.

Однако теорема Семереди ничего не говорит о том, насколько большой должна быть коллекция чисел для того, чтобы эти закономерности стали неизбежными. Он просто сказал, что для арифметической прогрессии любой выбранной длины обязательно существует множество чисел неизвестного размера, которое его содержит.

Более чем через два десятилетия после этого математики определили этот размер – доказав таким способом второй основной факт, касающихся арифметических закономерностей.

В 2001 году Тимоти Гауэрс из Кембриджского университета доказал, что если вы хотите гарантированно найти, допустим, арифметическую прогрессию из пяти членов, вам нужно множество чисел по меньшей мере определённого размера – и определил, какой это будет размер (описать точный размер сложно, в эту формулу входят огромные экспоненциальные числа).

Чтобы понять, что сделал Гауэрса, нужно понять, что имеют в виду математики, говоря о «размере» множества чисел и об идее «достаточно большого размера».

Во-первых, выберите интервал на числовой прямой, допустим, от 1 до 1000, или что-то более случайное, типа от 17 до 1016. Начало и конец интервала не имеют значения, важна только его длина. Затем определите ту долю чисел из этого интервала, которую вы хотите добавить в множество. К примеру, если вы создаёте множество из 100 чисел от 1 до 1000, то размер вашего множества составит 10% от интервала.

Доказательство Гауэрса работает вне зависимости от того, как вы выбираете числа из этого множества. Можно взять 100 первых нечётных чисел из диапазона от 1 до 1000, 100 первых чисел, заканчивающихся на 6, или даже 100 случайных чисел. И Гауэрс доказал, что вне зависимости от метода, как только множество займёт достаточно большое пространство (не обязательно 10%) в достаточно длинном интервале, в нём неизбежно появится арифметическая прогрессия из пяти членов. То же самое он доказал для арифметической прогрессии любой длины.

«После Гауэрса мы знаем, что если мне дадут арифметическую прогрессию любой длины, тогда любое подмножество» чисел какого-то определённого размера обязательно будет содержать эту прогрессию, сказала Пилюс.

Работа Пилюс похожа на достижение Гауэрса, только она сконцентрировалась на многочленных прогрессиях.

«Можно создавать большие множества чисел, не содержащие геометрических прогрессий. Но если дать себе немного свободы, и сдвинуть геометрическую прогрессию», создав многочленную прогрессию, то крупные множества, кажется, просто вынуждены содержать их, сказал Шон Прендивиль из Ланкастерского университета, работавший с Пилюс над многочленными прогрессиями.

В 1996 году Виталий Бергельсон и Александр Лейбман доказали, что при достижении достаточно большого размера множеством там обязательно должны появиться многочленные прогрессии – это был многочленный эквивалент работы Семереди. Однако, у математиков не было понятия о том, насколько большим должно быть «достаточно большое» множество.

Пилюс ответила на этот вопрос контринтуитивным способом – размышляя о том, какими свойствами должно обладать множество чисел, чтобы в нём не было таких закономерностей.

Борьба с закономерностями при помощи закономерностей

Пилюс хотела определить, насколько большим должно быть множество – какой процент чисел из интервала должен в нём содержаться – чтобы гарантировать, что оно будет содержать заданную многочленную прогрессию. Для этого она представила все способы, благодаря которым множество чисел может избежать появления в нём прогрессии – а потом доказала, что при превышении определённого размера не работают даже самые хитроумные из этих стратегий.

Эту задачу можно рассматривать как состязание. Допустим, кто-то просит вас создать множество, содержащее половину чисел от 1 до 1000. Вы выигрываете, если в множестве не будет первых четырёх членов многочленной прогрессии. Как бы вы подбирали числа?

Сара Пилюс из Оксфордского университета

Возможно, вы инстинктивно попытаетесь выбрать числа случайным образом. Но этот инстинкт будет ошибочным.

«Большинство множеств находятся в середине нормального распределения. Они содержат среднее количество многочленных прогрессий», — сказал Прендивиль. И это среднее значение гораздо больше требуемого от вас нулевого.

Это похоже на то, как если бы вы выбирали из всего населения планеты случайного человека, и получили такого, рост которого близок к среднему. Если ваша цель – найти более редкий экземпляр ростом более 2 м, вам нужно вести поиски более направленно.

Поэтому для выигрыша в состязании по выбору чисел вам нужен более организованный способ решать, какие числа включать в ваше множество из 500 штук. К примеру, можно заметить, что если выбирать только чётные числа, можно устранить вероятность того, что в множестве будут находиться многочленные прогрессии, содержащие нечётные числа. Прогресс! Естественно, таким способом вы увеличиваете вероятность того, что ваше множество содержит многочленные прогрессии, состоящие из чётных чисел.

Однако суть в том, что придумав структурированный способ выбора 500 чисел, можно устранить вероятность нахождения в множестве определённых многочленных прогрессий. Иначе говоря, нужно соблюдать закономерность, чтобы избежать закономерности.

Пилюс решила доказать, что при достижении определённого размера, даже очень хитроумно составленным множествам всё равно придётся включить в себя многочленные прогрессии. По сути, она хотела определить критическую точку, в которой вы, каждый раз избегая включения многочленных прогрессий одного типа, приходите к наличию многочленных прогрессий другого типа – как в случае с чётными и нечётными числами.

Для этого ей нужно было найти способ количественно оценить структуризацию множества.

Измерение структуры

До выхода работы Пилюс многие математики пытались понять, когда именно многочленные прогрессии появляется в множестве чисел. Этим занимались многие из весьма успешных математиков, но никто из них не смог достаточно сильно продвинуться на пути к выяснению размера множества, которого оно должно достичь, чтобы содержать многочленные прогрессии различной длины.

Главным препятствием для них было то, что математики не представляли, как именно можно охарактеризовать структуры, позволяющие избежать появления многочленных прогрессий. Была одна потенциальная техника для этого, но когда Пилюс начинала работать в этой области, её нельзя было применить к вопросам, касающимся многочленных прогрессий.

Эта техника появилась в работе Гауэрса от 2001 года по арифметическим прогрессиям. Гауэрс создал тест, назвав его «нормой Гаэурса», обнаруживающий структуры определённого вида в множестве чисел. Тест выдаёт одно число, определяющее количество структурности в множестве – то есть, он численно показывает, насколько далеко множество отошло от простого набора случайных чисел.

«Понятие ”множество выглядит случайным” не является чётко определённым с математической точки зрения», — сказал Грин. Гауэрс нашёл способ количественно охарактеризовать это понятие.

Множество может быть более или менее структурированным. Множества, содержащие случайные числа, не имеют структуры, поэтому с большой вероятностью содержат числовые закономерности. У таких множеств норма Гауэрса низкая. Множества, содержащие только нечётные числа, или только числа, делящиеся на 10, имеют рудиментарную структуру. Легко доказать, что при превышении определённого размера в множествах такой простой структуры также появятся различные закономерности.

Тяжелее всего работать с множествами очень сложных структур. Они могут выглядеть случайными, однако при этом быть построенными по какому-то очень хитрому правилу. Их норма Гауэрса высока, и они дают наилучшие шансы систематически избегать закономерностей при росте размера множества.

Поскольку Гауэрс использовал эти техники для поисков ответы на вопросы, связанные с арифметическими прогрессиями, их нельзя было применить к вопросам, касающимся многочленных прогрессий. Арифметические прогрессии имеют равные промежутки, а числа в многочленных прогрессиях очень активно скачут. Нормы Гауэрса были полезными для изучения многочленных прогрессий так же, как триммер для травы для очистки старой краски с дома: идея похожая, хотя для этой работы и не совсем подходит.

В новом доказательстве Пилюс использовала базовую идею нормы Гауэрса для создания нового способа анализа структур, связанных с многочленными прогрессиями. Она использовала технику «понижения градуса» для доказательства того, что при разбирательствах с интересующими её многочленными прогрессиями стоит беспокоиться только о простых структурах с низкой нормой Гауэрса. Дело в том, что многочленные прогрессии настолько сильно меняются при переходе от одного члена к другому, что они неизбежно прорываются через менее прочные числовые препятствия – как слон, продирающийся через витрины наружу из посудной лавки.

Формулу Пилюс тяжело описать простыми терминами. В ней участвует двойной логарифм длины изначального интервала, из которого вы выбираете числа для своего множества. Полученный ею минимальный размер не обязательно будет самым малым из всех возможных – в будущих работах может обнаружиться, что истинный порог находится ещё ниже. Но до появления её доказательства у математиков вообще не было количественного понимания появления гарантии наличия многочленных прогрессий.

«Она стала первым человеком, показавшим, насколько большим должен быть размер множества», — сказал Прендивиль.

Доказательство Пилюс количественно отвечает на один вопрос, связанный с многочленными прогрессиями. Теперь математики используют его в надежде получить ответ на другой вопрос – касательно того, когда многочленные прогрессии появляются в множествах, целиком состоящих из простых чисел, наиболее важных чисел в математике, упорно сопротивляющихся каким бы то ни было последовательностям. До появления этого доказательства у математиков не было представления о том, как подойти к этому вопросу.

«Есть надежда, что некоторые из аргументов моей работы можно будет применить в области простых чисел», — сказала Пилюс.

Источник

Закономерности

Закономерности, как и свойства предметов связаны с математикой и с логикой. Зная закономерность, ты точно можешь знать, что будет дальше. После четверга точно будет пятница, после 10 часов утра будет 11 часов утра. Последовательность действий, явлений, свойств или событий в закономерности всегда определена, то есть мы точно знаем что будет дальше.

Типы закономерностей

Существует несколько типов закономерностей: убывающие, возрастающие, циклические и сложные закономерности. Давайте познакомимся с каждой подробнее.

Возрастающая закономерность

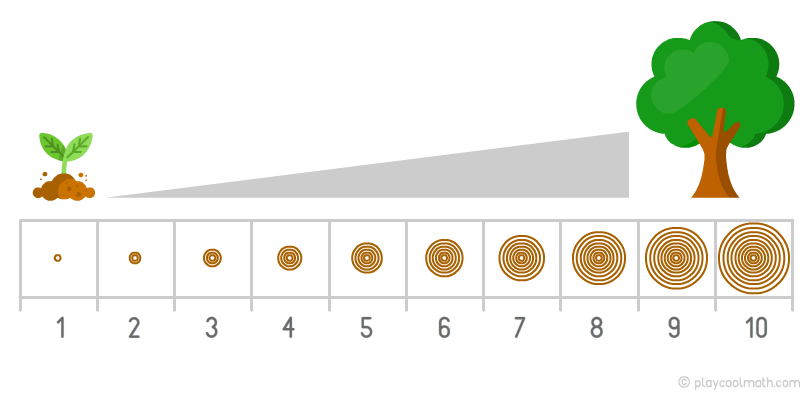
Например, дерево растет и на его стволе каждый год добавляется одно новое кольцо. Этот процесс называется простой возрастающей закономерностью. В этой закономерности легко вычислить, сколько колец будет через 2 года или через 10 лет. Количество колец в стволе соответствует возрасту дерева.

Убывающая закономерность

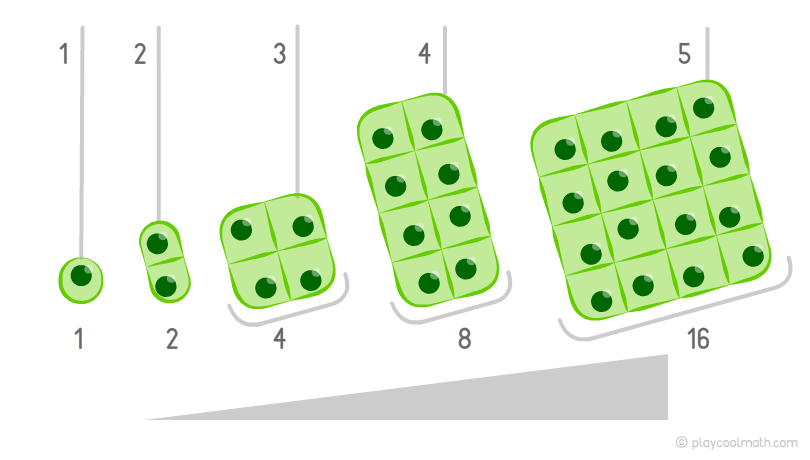
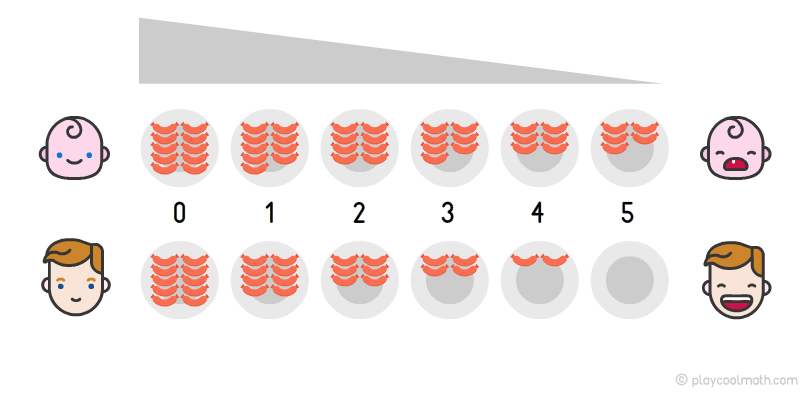
Представьте соревнования по поеданию сосисок на скорость, в которых участвуют два участника. У каждого по 10 сосисок на тарелке (это столько, сколько у тебя пальцев на руках). Первый съедает одну сосиску за минуту, а второй съедает 2 сосиски за минуту. Ясно, что второй участник соревнований победит, так как он съедает больше сосисок за минуту, чем первый участник. Но нам важно увидеть закономерность. На рисунке мы можем увидеть, как в каждой тарелке уменьшается количество сосисок. Этот процесс называется убывающей закономерностью. Второй участник съел всю тарелку сосисок за пять минут и победил!

Циклическая закономерность

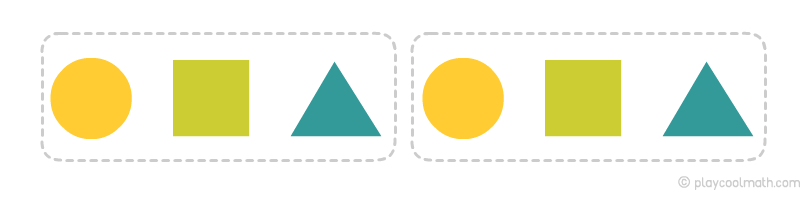
Рассмотрим пример с предметами разной формы. На рисунке ты видишь цепочку из разного количества предметов. Попробуй найти закономерность на рисунке ниже. Продолжи цепочку.

Предметы повторяются через каждые три ячейки. Зная закономерность, мы можем предположить, какие предметы будут дальше. За последним звеном будет треугольник, затем круг, далее квадрат.

Сложные закономерности

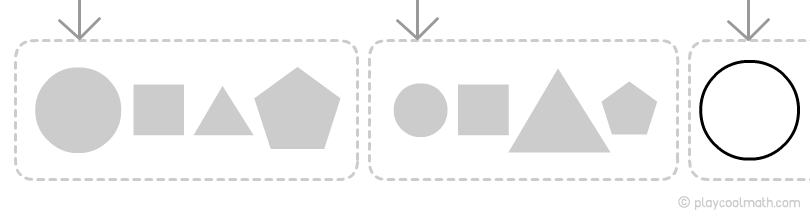
Рассмотрим пример закономерностей на одной и той же цепочке, но будем искать закономерности в зависимости от свойства звеньев. Попробуй найти следующее звено в примере ниже.

Закономерность по форме

Видим, как чередуются звенья цепочки. Точно знаем, что по форме следующим будет круг, обозначим его как большой круг

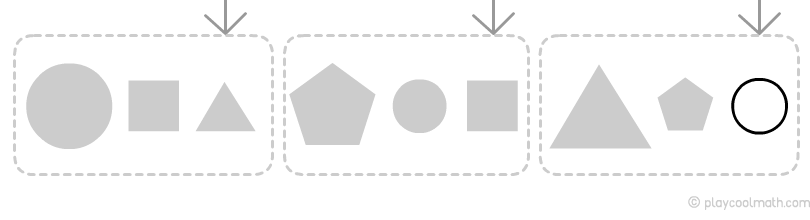
Закономерность по размеру

Видим, как чередуются звенья цепочки: большая и затем две маленькие фигуры, то есть следующей будет маленькая фигура.

Закономерность по цвету

Получилась самая длинная закономерность в цепочке, выделим ее и определим, какой будет следующий цвет.

Как видишь, закономерность зависит от свойств элементов цепочки. Для одной и той же цепочки мы нашли различные закономерности в зависимости от свойства. Объединим полученные результаты и узнаем, какое звено будут следующим.

Алгоритм поиска закономерностей

Давайте еще раз повторим все шаги для выявления закономерностей.

Источник