Запишите на математическом языке чему равно расстояние между точками а и б
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Предупреждение
Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
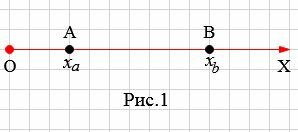 |
Расстояние между точками A и В равно:
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
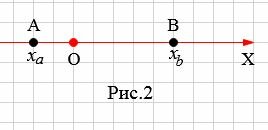 |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
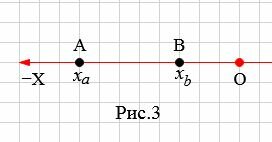 |
B этом случае рассояние между точками A и B равно:
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
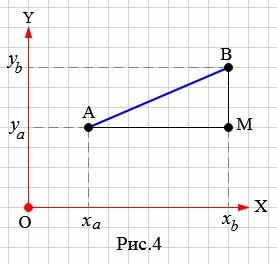 |
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
Тогда, учитывая (8), получим:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
 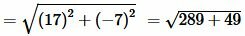 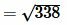 , , |
Ответ: 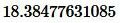
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
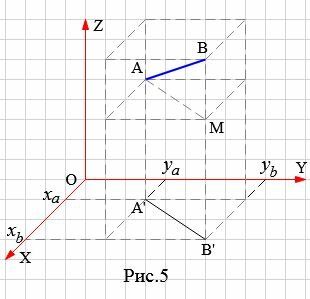 |
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
Но AM=A’B’. Тогда из (10) и (11) следует:
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
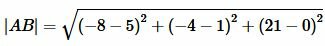 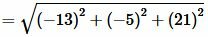 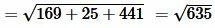 , , |
Ответ: 
§ 3. Что такое математическая модель
Перейдите от словесной модели к математической:
3.1. а) Произведение чисел х и у равно 9;
б) частное от деления числа а на число b равно 2;
в) числа b и с равны;
г) числа 2р и 3q равны.
3.2. а) Число а на 18 больше числа b;
б) число b на 39 меньше числа с;
в) число х в 6 раз больше числа у;
г) число а в 29 раз меньше числа b.
3.3. а) Сумма чисел а и б равна 43;
б) разность чисел m и n равна 214;
в) сумма чисел а и b на 6 меньше их произведения;
г) разность чисел р и q на 17 больше их частного.
3.4. Для чисел а, b, с, d:
а) сумма первых двух чисел равна разности четвёртого и третьего чисел;
б) разность первого и четвёртого чисел равна сумме второго и третьего чисел;
в) первое число равно сумме трёх остальных;
г) сумма первых двух чисел равна удвоенной разности двух последних.
Изобразите графическую модель ситуации:
3.5. а) На координатной прямой точка а расположена левее точки b;
б) на координатной прямой точка а расположена правее точки b.
Запишите на математическом языке, чему равно расстояние между точками а и b.
Составьте математическую модель данной ситуации:
3.7. Первый рабочий выполняет задание за t ч, а второй такое же задание — за υ ч, при этом первый работает на 3 ч больше, чем второй.
3.8. Три килограмма яблок стоят столько же, сколько два килограмма груш. При этом известно, что 1 кг яблок стоит х р., а 1 кг груш стоит у р.
3.9. Стоимость стакана мандаринового сока а р., а стакана виноградного сока — b р. Известно, что 5 стаканов виноградного сока стоят столько же, сколько 6 стаканов мандаринового сока.
3.11. Первое число равно х, второе в 1,5 раза больше первого. Если к первому числу прибавить 3,7, а из второго числа вычесть 5,36, то получатся одинаковые результаты.
3.13. На стройке работало 5 бригад по а человек в каждой и 3 бригады по b человек в каждой, при этом всего на стройке работало m человек.
3.14. Первое число равно с, второе число в 1,4 раза больше первого. Если из второго числа вычесть 5,2, а к первому прибавить 4,8, то получатся равные результаты.
3.15. В первом букете d роз, а во втором в 4 раза больше, чем в первом. Когда к первому букету добавили 15 роз, а ко второму — 3 розы, в обоих букетах роз стало поровну.
3.17. У Миши х марок, а у Андрея у марок. Если Миша отдаст Андрею 8 марок, то у Андрея станет марок вдвое больше, чем останется у Миши.
3.18. Автомобиль проехал х км по шоссе и у км по просёлочной дороге, причём по шоссе он проехал большую часть пути.
а) Сколько всего километров проехал автомобиль по шоссе и просёлочной дороге?
б) На сколько больше километров он проехал по шоссе, чем по просёлочной дороге?
в) Во сколько раз путь по просёлочной дороге короче пути по шоссе?
г) Какое время затратил автомобиль на весь путь, если он ехал со скоростью 40 км/ч; υ км/ч; 60 км/ч по шоссе и 30 км/ч по просёлочной дороге?
Расстояние между точками на координатной прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
10 : 2 = 5, значит |AC| = |CB| = 5.
Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
Ответ. Координата точки C — 16.
Запишите на математическом языке чему равно расстояние между точками а и б
Найдите все целочисленные значения параметра а, при каждом из которых система
имеет единственное решение.
Следовательно, данная система имеет единственное решение тогда и только тогда, когда второе уравнение системы имеет единственное решение на отрезке 1 ≤ x ≤ 5.
Рассмотрим квадратичную функцию
Её график — парабола, направленная ветвями вверх. Поскольку свободный при любом a, то корни этой функции имеют разные знаки. Известно, что в этом случае единственный положительный корень функции
лежит на отрезке 1 ≤ x ≤ 5 тогда и только тогда, когда
и
Получаем систему
Поскольку любое решение полученного неравенства должно удовлетворять условию то есть
и по условию a — целое число, то решениями неравенства могут быть только
Из этих условий проверкой получаем все решения: −2, ±1, 0.
Ваше рассуждение было бы верным, если бы во втором уравнении системы присутствовала переменная .
Найдите все целочисленные значения параметра а, при каждом из которых система
имеет единственное решение.
Следовательно, данная система имеет единственное решение тогда и только тогда, когда второе уравнение системы имеет единственное решение на отрезке 2 ≤ x ≤ 5.
Рассмотрим квадратичную функцию
Её график — парабола, направленная ветвями вверх. Поскольку свободный член при любом a, то корни этой функции имеют разные знаки. Известно, что в этом случае единственный положительный корень функции
лежит на отрезке 2 ≤ x ≤ 5 тогда и только тогда, когда
и
Получаем систему
Поскольку любое решение полученного неравенства должно удовлетворять условию то есть
и по условию a — целое число, то решениями неравенства могут быть только
Из этих условий проверкой получаем все решения: −2, ±1, 0.
Аналоги к заданию № 512340: 512382 Все
Извините, не совсем понятно почему функция от 2 меньше либо равно 0,а функция от 5 больше либо равно 0.Объясните,пожалуйста.Спасибо.
Андрей, попробуйте нарисовать параболу с описанными свойствами: ветви вверх, с отрицательным свободным членом, положительный корень лежит между числами 2 и 5. И вы сами увидите ответ на свой вопрос
При каждом а решите систему уравнений
Запишем второе уравнение в виде
Геометрический смысл уравнения состоит в том, что сумма расстояний от точек до точек
и
равно
Поскольку расстояние между точками
и
тоже равно
это означает, что точка
должна лежать на отрезке, соединяющем точки
и
Другими словами, она удовлетворяет уравнению
и условию
Таким образом, исходная система равносильна системе
Подставив 2а в первое уравнение, получаем
Поскольку функция возрастающая (как сумма двух возрастающих), каждое значение она принимает ровно один раз. Поэтому решение
— единственное, ему соответствует
Ответ: если то
при остальных а нет решений.
А как нашли, что х=5/2?
угадали корень уравнения:
Найдите все неотрицательные значения a, при каждом из которых система уравнений
имеет единственное решение.
Первому уравнению системы удовлетворяют те и только те точки которые лежат на отрезке AB прямой, соединяющей точки
и
поскольку уравнение задаёт множество точек
сумма расстояний от каждой из которых до точек А и В равна
что равно длине отрезка АВ.
Второму уравнению системы удовлетворяют те и только те точки которые лежат на прямой
параллельной оси абсцисс и проходящей через точку
По условию Если
то точки В и О совпадают, и система не имеет решений. Для
условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой O или с точкой В, то условие задачи выполнено.
Решим неравенство Имеем:
Ответ:
Задача станет интереснее, если отказаться от условия неотрицательности параметра. При a Ответ:
Отсутствует случай a
Найдите все значения параметра при каждом из которых система
имеет единственное решение.
Уравнение означает, что сумма расстояний от точки
до точек
и
равна
но эта сумма расстояний всегда больше, чем
если только точка
не лежит на отрезке с концами
и
Значит, множество решений при
— это отрезок с концами
и
При
множество решений — это
Множество решений неравенства — круг на плоскости с координатами
с центром в начале координат и радиусом
Отсюда получаем необходимое условие существование единственного решения — отрезок с концами
и
должен пересекаться с данным кругом в единственной точке. Это возможно при
(когда отрезок превращается в точку), а также когда отрезок касается границы круга. Из симметрии точка касания лежит в середине этого отрезка. Расстояние от середины отрезка до начала координат равно
В случае касания это расстояние должно совпадать с радиусом круга, откуда получаем уравнение
Таким образом, система имеет единственное решение при
и
Ответ:




