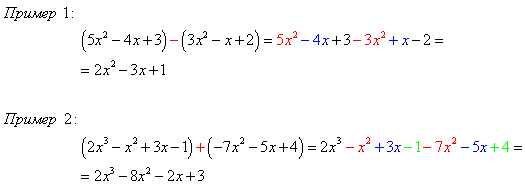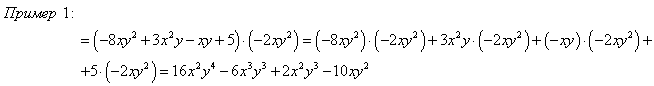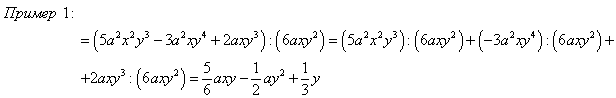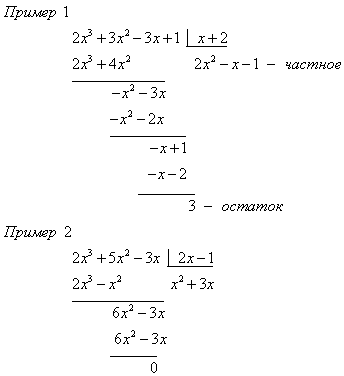Заполните таблицу считая что f x

Заполните таблицу считая что f x

Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x 4 +5x 3 +x 2 −11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу:

Следующую ячейку заполним по такому принципу: 1 ⋅ 5 + 5 = 10 :

Аналогично заполним и четвертую ячейку второй строки: 1 ⋅ 10 + 1 = 11 :

Для пятой ячейки получим: 1 ⋅ 11 + 0 = 11 :

И, наконец, для последней, шестой ячейки, имеем: 1 ⋅ 11 + ( −11) = 0 :

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x 4 +5x 3 +x 2 −11 на x−1. Естественно, что так как степень исходного многочлена 5x 4 +5x 3 +x 2 −11 равнялась четырём, то степень полученного многочлена 5x 3 +10x 2 +11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x 4 +5x 3 +x 2 −11 на x−1.
В нашем случае остаток равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю.
Можно сформулировать вывод и в такой форме: так как значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю, то единица является корнем многочлена 5x 4 +5x 3 +x 2 −11.

2. Найдите неполное частное, остаток от деления многочлена

Источник

Использование методики взаимопередачи тем при изучении математики

Наша школа занимается по интегрированным образовательным программам, специально разработанных для сети Назарбаев Интееллектуальных школ.Здесь приводятся описание методики ВПТ по теме «Алгебраические выражения».

Просмотр содержимого документа
«Использование методики взаимопередачи тем при изучении математики»

Составитель: Аймжанова Агилаш Адигановна,

Методические рекомендации к использованию методики взаимопередачи тем при изучении математики ( из опыта работы)- Актобе, 2015.- 16с.

Рецензент: Кужакова С.Ж-заведующая кафедрой математики NIS ФМН

Данный сборник предназначен для учителей математики и содержит в себе описание методики взаимопередачи тем, а также применение данной методики при изучении раздела «Алгебраические выражения» в 11 классе.

Использование различных методик коллективных учебных занятий, таких как: методика Ривина, методика, обратная ривинской, взаимообмен заданиями, методика взаимопередачи тем, взаимотренаж и другие, позволяют учителю разнообразнее проводить уроки, тем самым повышая интерес к предмету и личную ответственность учащихся за свое обучение.

Описание методики ВПТ

Методика взаимопередачи тем (ВПТ) предназначена для организации изучения теоретического учебного материала на основе работы учащихся в парах сменного состава.

Основная идея организации проста.

1) Ученикам необходимо освоить какой-либо раздел (блок) учебной программы. Каждый ученик должен одну или несколько тем изучить самостоятельно, а часть тем получить от других учеников. Соответственно, темы, которые он освоил самостоятельно, он должен передать своим товарищам. Самостоятельно изученные темы в обязательном порядке сдаются учителю.

Под темой понимается определённым образом оформленный текст, к которому подобраны три группы задач, упражнений, вопросов и т.д.

2)Прорабатывая текст, ученик в итоге получает подробнейший (поабзацный) план изучаемой темы и решения задач (вопросов) первой и второй групп этой темы. И только после этого тема сдаётся учителю. Учитель проверяет не только уровень освоения темы, но и готовит ученика к роли учителя, которую ему придётся выполнять при обучении другого.

3)Взаимодействие учеников организуется следующим образом. Один ученик восстанавливает другому по частям (по своему плану) содержание своей темы, после каждой части проверяет уровень понимания и задает вопросы (или предлагает решить задачи) первой группы. После этого ученик, который находится в позиции учащегося, записывает заголовок этой части. В результате совместной работы у напарника в тетради появляется подробнейший план темы. После этого ученики меняются ролями. Обучив друг друга, каждый из учеников самостоятельно приступает к выполнению упражнений второй группы. А далее они проверяют друг друга.

4) На следующем этапе ученики прорабатывают материал третьей группы.

Задания группам рекомендуется давать разного уровня.

Теории многочленов в школьном курсе математики уделено немало внимания. Учащиеся знакомятся с этими понятиями еще в 7 классе общеобразовательной программы. Наша школа работает по Интегрированной образовательной программе, где основное внимание также уделяется развитию навыков самостоятельного изучения нового материала, особенно у учащихся старших классов.

Привожу примеры использования методики ВПТ по разделу «Алгебраические выражения» в 11 классе.

Тема 1: Многочлен. Форма и описание.Действия над многочленами.

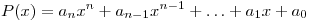
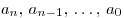
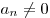
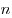
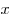
Определение1.Выражение вида , где — некоторые числа и , называется многочленом степени от .

Наивысшая степень переменной, входящих в многочлен одночленов называется степенью многочлена. Многочлен с одной переменной, старший коэффициент которого равен 1, называется приведенным.

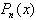
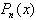
Определение 2.Корнем многочлена с одной переменной , называют те значения переменной x, при которых многочлен обращается в ноль. Иными словами, решение уравнения =0.

Определение3.Стандартным видом многочлена с одной переменной называется запись этого многочлена в порядке убывания степеней одночленов, каждый из которых записан в стандартном виде и среди которых нет подобных.

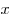
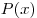
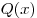
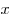
Определение 5.Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях . Многочлены и тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях этих многочленов одинаковы.

Определение 4. Симметрический многочлен — это такой многочлен, который не изменяется при любых перестановках, входящий в него переменных.

Симметрический многочлен можно записать так: P(x, y) = P(y, x).

Например, x 2 y + xy 2 или а+b- симметрические многочлены.

Если степени всех членов многочлена одинаковы, то этот многочлен называют однородным.

Сумма и разность многочленов

Для того, чтобы преобразовать сумму и разность многочленов в многочлен стандартного вида, надо:
1) раскрыть скобки;
2) привести подобные члены

Умножение и деление многочлена на одночлен

Каждый член многочлена умножить на одночлен и полученные произведения сложить (с учетом знаков слагаемых).

Деление многочлена на одночлен производится по аналогичному правилу.

Деление многочленов выполняется «углом», если степень многочлена-делимого не меньше степени многочлена делителя.

1. Выбрать среди предложенных ниже алгебраических выражений те, которые являются многочленами:

2. Пусть f(x)=найдите и запишите в стандартном виде:

3. Что называют корнем многочлена?

Заполните таблицу, считая, что f(x) и g(x) многочлены:

Источник

Схема Горнера

Схема Горнера – способ деления многочлена

Задача решена, осталось только записать ответ:

Полученный результат означает, что

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0\cdot x^2 +4x-17)+4=(x+3)(x^3+4x-17)+4$$

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 \cdot (-3)^3-5 \cdot (-3)-47=4.$$

Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.

Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.

Учитывая равенство (2), равенство (1) можно переписать в такой форме:

С учетом равенства (4), равенство (3) перепишем в такой форме:

Полученный результат можно записать так (это продолжение равенства (6)):

Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:

Из таблицы следует вывод, полученный нами ранее с подробным решением:

Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Таблица производных функций

10 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое производная и зачем она нужна

Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:

Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.

Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.

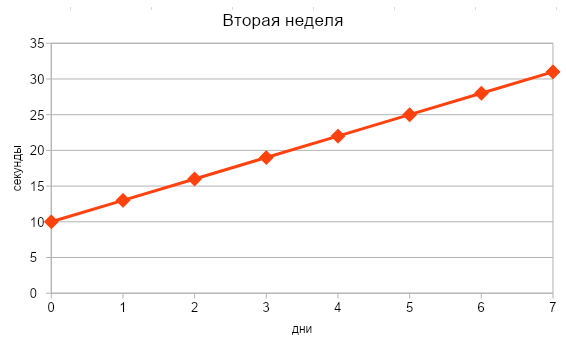
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:

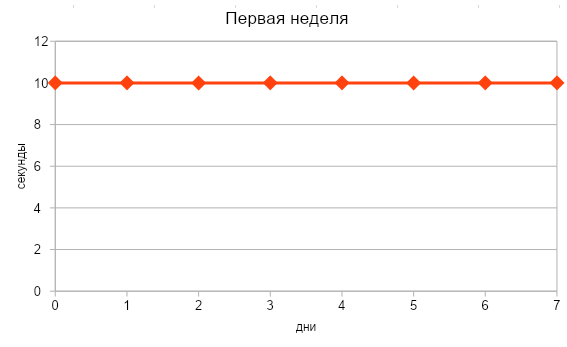
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.

Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.

Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.

Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.

Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.

Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.

Производные основных элементарных функций

Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Приведем несколько формул, которых достаточно для решения большинства задач.

Источник

Вариант №5 с сайта К. Полякова

Решение вариант №5 ЕГЭ с сайта Константина Полякова

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите длину кратчайшего пути из пункта Г в пункт В.

Ответ: 25

Логическая функция F задаётся выражением

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (x == (not z))

В фрагменте базы данных представлены сведения о родственных отношениях.
Определите мужчину, который впервые стал отцом в самом раннем возрасте, и запишите в ответе его идентификатор (ID).

Ответ: 367

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, К, О, Н, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:

Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОРАН?

Ответ: 15

Ответ: 86

Определите, при каком наименьшем целом введённом значении переменной d программа выведет число 192.

var s, n, d: integer; begin readln (d); s := 0; n := 0; while n using namespace std; int main() < int d, s = 0, n = 0; cin >> d; while (n

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 70 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 4 раза выше и частотой дискретизации в 3,5 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер файла в Мбайт, полученного при повторной записи.

Ответ: 160

Юрий составляет 4-буквенные слова из букв П, Р, И, К, А, З. Каждую букву можно использовать не более одного раза, при этом в слове нельзя использовать более одной гласной.

Сколько различных кодов может составить Юрий?

Ответ: 216

Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите среднее значение измерений, в которых температура не превышала 15 градусов. В ответе запишите только целую часть получившегося числа.

Ответ: 12

С помощью текстового редактора определите, сколько раз, не считая сносок, встречаются личные местоимения (я, ты, он, она, оно), без учета регистра в тексте А.П. Чехова «Воры» (файл 10-1.docx). В ответе укажите только число.

Ответ: 141

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 6 символов и содержащий только символы из 7-буквенного набора А, В, Е, К, М, Н, О. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 10 байт.
Определите объём памяти в байтах, необходимый для хранения сведений о 100 пользователях.

Ответ: 1300

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

Дана программа для исполнителя Редактор:

Какая строка получится в результате применения приведённой программы к строке вида 1…13…3 (2018 единиц и 2050 троек)?

s = 2018*’1’+2050*’3′ while «111» in s: s = s.replace( «111», «2», 1 ) s = s.replace( «222», «3», 1 ) s = s.replace( «333», «1», 1 ) print(s)

Ответ: 332113

На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, не проходящих через город Е?

Ответ: 30

записали в системе счисления с основанием 3.
Найдите сумму цифр в этой записи. Ответ запишите в десятичной системе.

Ответ: 18

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наименьшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х )?

Определите количество натуральных значений n из отрезка [1; 1000], для которых все цифры значения F(n) чётные.

Ответ: 33

Рассматривается множество целых чисел, принадлежащих отрезку [1100;11000], которые делятся на 6 и не делятся на 7, 13, 17 и 23.
Найдите количество таких чисел и максимальное из них. В ответе запишите два числа через пробел: сначала количество, затем максимальное число.

a = [n for n in range(1100,11000+1) if (n%6==0 and n%7!=0 and n%13!=0 and n%17!=0 and n%23!=0)] print(len(a),max(a))

Ответ: 1178 10992

Квадрат разлинован на N×N клеток (1

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней.
В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 1 (задание 19). Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 2 (задание 20). Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
Вопрос 3 (задание 21). Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

def f(x,y,p): if x+y>=40 and p==3: return 1 elif x+y =40 and p==4: return 1 elif x+y 40: return 0 elif p%2==1: return f(x+1,y,p+1)+f(x*2,y,p+1)+f(x,y+1,p+1)+f(x,y*2,p+1) else: return f(x+1,y,p+1)*f(x*2,y,p+1)*f(x,y+1,p+1)*f(x,y*2,p+1) for i in range (1,1000): if f(9,i,1): print(i)

def f(x,y,p): if x+y>=40 and (p==3 or p==5): return 1 elif x+y 40: return 0 elif p%2==0: return f(x+1,y,p+1)+f(x*2,y,p+1)+f(x,y+1,p+1)+f(x,y*2,p+1) else: return f(x+1,y,p+1)*f(x*2,y,p+1)*f(x,y+1,p+1)*f(x,y*2,p+1) for i in range (1,1000): if f(9,i,1): print(i)

Ответ:

Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 15.

var x, a, b: integer; begin readln(x); a:=0; b:=1; while x > 0 do begin a:= a + 1; b:= b*(x mod 10); x:= x div 10; end; writeln(a); write(b); end.

x = int(input()) a = 0 b = 1 while x > 0: a = a + 1 b = b*(x % 10) x = x // 10 print(a) print(b)

for x_ in range(1,1001): x = x_ a = 0 b = 1 while x > 0: a = a + 1 b = b*(x % 10) x = x // 10 if a==3 and b==15: print(x_) break

Ответ: 135

Исполнитель Калькулятор преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:

Программа для исполнителя Калькулятор – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 18?

Источник