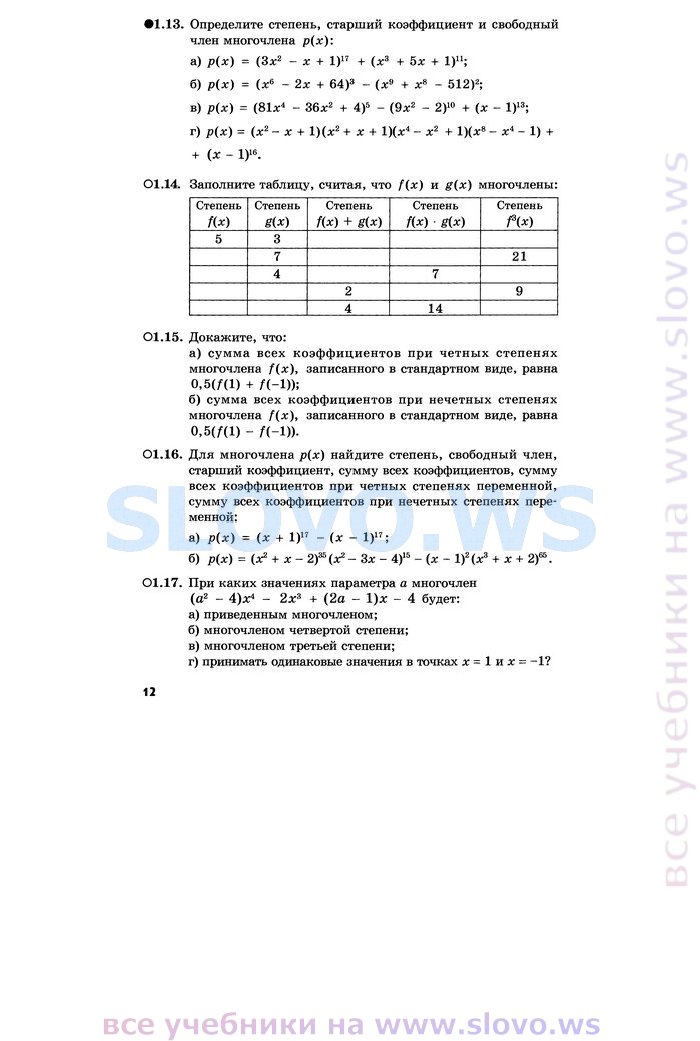
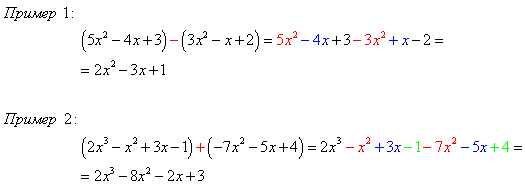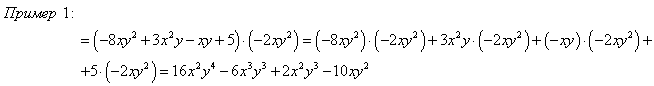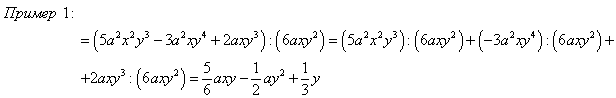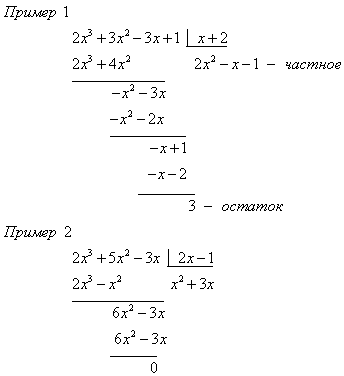Заполните таблицу считая что fx и gx многочлены
Использование методики взаимопередачи тем при изучении математики
Наша школа занимается по интегрированным образовательным программам, специально разработанных для сети Назарбаев Интееллектуальных школ.Здесь приводятся описание методики ВПТ по теме “Алгебраические выражения”.
Просмотр содержимого документа
«Использование методики взаимопередачи тем при изучении математики»
Составитель: Аймжанова Агилаш Адигановна,
Методические рекомендации к использованию методики взаимопередачи тем при изучении математики ( из опыта работы)- Актобе, 2015.- 16с.
Рецензент: Кужакова С.Ж-заведующая кафедрой математики NIS ФМН
Данный сборник предназначен для учителей математики и содержит в себе описание методики взаимопередачи тем, а также применение данной методики при изучении раздела «Алгебраические выражения» в 11 классе.
Использование различных методик коллективных учебных занятий, таких как: методика Ривина, методика, обратная ривинской, взаимообмен заданиями, методика взаимопередачи тем, взаимотренаж и другие, позволяют учителю разнообразнее проводить уроки, тем самым повышая интерес к предмету и личную ответственность учащихся за свое обучение.
Описание методики ВПТ
Методика взаимопередачи тем (ВПТ) предназначена для организации изучения теоретического учебного материала на основе работы учащихся в парах сменного состава.
Основная идея организации проста.
1) Ученикам необходимо освоить какой-либо раздел (блок) учебной программы. Каждый ученик должен одну или несколько тем изучить самостоятельно, а часть тем получить от других учеников. Соответственно, темы, которые он освоил самостоятельно, он должен передать своим товарищам. Самостоятельно изученные темы в обязательном порядке сдаются учителю.
Под темой понимается определённым образом оформленный текст, к которому подобраны три группы задач, упражнений, вопросов и т.д.
2)Прорабатывая текст, ученик в итоге получает подробнейший (поабзацный) план изучаемой темы и решения задач (вопросов) первой и второй групп этой темы. И только после этого тема сдаётся учителю. Учитель проверяет не только уровень освоения темы, но и готовит ученика к роли учителя, которую ему придётся выполнять при обучении другого.
3)Взаимодействие учеников организуется следующим образом. Один ученик восстанавливает другому по частям (по своему плану) содержание своей темы, после каждой части проверяет уровень понимания и задает вопросы (или предлагает решить задачи) первой группы. После этого ученик, который находится в позиции учащегося, записывает заголовок этой части. В результате совместной работы у напарника в тетради появляется подробнейший план темы. После этого ученики меняются ролями. Обучив друг друга, каждый из учеников самостоятельно приступает к выполнению упражнений второй группы. А далее они проверяют друг друга.
4) На следующем этапе ученики прорабатывают материал третьей группы.
Задания группам рекомендуется давать разного уровня.
Теории многочленов в школьном курсе математики уделено немало внимания. Учащиеся знакомятся с этими понятиями еще в 7 классе общеобразовательной программы. Наша школа работает по Интегрированной образовательной программе, где основное внимание также уделяется развитию навыков самостоятельного изучения нового материала, особенно у учащихся старших классов.
Привожу примеры использования методики ВПТ по разделу «Алгебраические выражения» в 11 классе.
Тема 1: Многочлен. Форма и описание.Действия над многочленами.
Определение1.Выражение вида 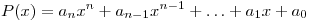
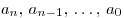
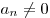
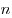
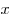
Наивысшая степень переменной, входящих в многочлен одночленов называется степенью многочлена. Многочлен с одной переменной, старший коэффициент которого равен 1, называется приведенным.
Определение 2.Корнем многочлена с одной переменной 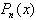
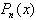
Определение3.Стандартным видом многочлена с одной переменной называется запись этого многочлена в порядке убывания степеней одночленов, каждый из которых записан в стандартном виде и среди которых нет подобных.
Определение 5.Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях 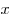
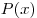
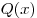
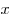
Определение 4. Симметрический многочлен — это такой многочлен, который не изменяется при любых перестановках, входящий в него переменных.
Симметрический многочлен можно записать так: P(x, y) = P(y, x).
Например, x 2 y + xy 2 или а+b- симметрические многочлены.
Если степени всех членов многочлена одинаковы, то этот многочлен называют однородным.
Сумма и разность многочленов
Для того, чтобы преобразовать сумму и разность многочленов в многочлен стандартного вида, надо:
1) раскрыть скобки;
2) привести подобные члены
Умножение и деление многочлена на одночлен
Каждый член многочлена умножить на одночлен и полученные произведения сложить (с учетом знаков слагаемых).
Деление многочлена на одночлен производится по аналогичному правилу.
Деление многочленов выполняется “углом”, если степень многочлена-делимого не меньше степени многочлена делителя.
1. Выбрать среди предложенных ниже алгебраических выражений те, которые являются многочленами:
2. Пусть f(x)=найдите и запишите в стандартном виде:
3. Что называют корнем многочлена?
Заполните таблицу, считая, что f(x) и g(x) многочлены:
Алгебра и начала математического анализа, 11 класс. Часть 2 из 2. Задачник (А. Г. Мордкович и др.) 2009
Страница № 012.
Учебник: Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович и др. под ред. А. Г. Мордковича. — 3-е изд., стер. — М. : Мнемoзина, 2009. — 264 с.: ил.
OCR-версия страницы из учебника (текст страницы, которая находится выше):
#1.13. Определите степень, старший коэффициент и свободный член многочлена р(х):
01.14. Заполните таблицу, считая, что f(x) и g(x) многочлены:
а) сумма всех коэффициентов при четных степенях многочлена f(x), записанного в стандартном виде, равна 0,5(/(1) + /4-1));
01.16. Для многочлена р(х) найдите степень, свободный член, старший коэффициент, сумму всех коэффициентов, сумму всех коэффициентов при четных степенях переменной, сумму всех коэффициентов при нечетных степенях переменной:
а) приведенным многочленом;
б) многочленом четвертой степени;
в) многочленом третьей степени;
Учебник: Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович и др. под ред. А. Г. Мордковича. — 3-е изд., стер. — М. : Мнемoзина, 2009. — 264 с.: ил.
Справочные таблицы по теме: “Многочлены”
Число 0 называется нулевым одночленом
Степенью одночлена называется сумма показателей букв, входящих в одночлен. Если одночленом является число, не равное нулю, то его степень считается равной нулю
Число 0 степени не имеет
– одночлен шестой степени (3+2+1=6);
– одночлен четвертой степени (1+3=4);
7 – одночлен нулевой степени
– одночлен третьей степени относительно переменной х
;– одночлены в стандартном виде
Действия над одночленами
Сложение и вычитание
Возведение в степень
Многочленом называется сумма конечного числа одночленов (каждый из которых называется членом многочлена).
Одночлены также считаются многочленами, состоящими из одного члена
Число 0 называется нулевым многочленом
– многочлены, состоящие из одного члена
Степенью ненулевого многочлена называется наибольшая степень из степеней его членов (одночленов)
Нулевой многочлен (0) степени не имеет
– многочлен третьей степени (так как наибольшая степень у члена abc – третья)
Действия над многочленами
Тождественно равные многочлены
Определение. Два многочлена называются тождественно равными, если они принимают равные значения при всех значениях букв (иногда тождественное равенство обозначается знаком « »
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобку
Использование формул сокращенного умножения и др. формул
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ И РАЗЛОЖЕНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ НА МНОЖИТЕЛИ
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе и плюс квадрат второго числа
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго и плюс куб второго числа
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго и плюс куб второго числа
Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат разности этих чисел
Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат суммы этих чисел
Квадрат суммы нескольких выражений равен сумме квадратов всех слагаемых плюс все удвоенные произведения каждого выражения на каждое последующее
Разложение на множители квадратного трехчлена и некоторых многочленов
Если для многочлена f ( x ) мы знаем только один корень (т.е – один из корней уравнения f ( x )=0), тогда этот многочлен делится без остатка на и его можно записать так:
Где g ( x ) можно найти, например, деление «уголком» f ( x ) на
Обобщение некоторых формул сокращенного умножения
Для нечетных натуральных n
Степень двучлена ( бином Ньютона)
где коэффициенты этого разложения можно взять из таблицы именуемой треугольник Паскаля
В этой таблице в каждой строке по краям стоят единицы, а каждой из остальных чисел равно сумме двух чисел, находящихся над ним слева и справа
МНОГОЧЛЕН ОТ ОДНОЙ ПЕРЕМЕННОЙ
где числовые коэффициенты
Член называется старшим членом многочлена P ( x ), а a n – его свободным членом
– многочлен третьей степени
– многочлен второй степени
Тождественно равные многочлены от одной переменной
Определение. Два многочлена называются тождественно равными, если они принимают равные значения при всех значениях переменной
(иногда тождественное равенство обозначается знаком «»)
Свойства тождественного равенства многочленов от одной переменной
Если многочлен P ( x ) тождественно равен нулю (т.е. принимает нулевые значения при всех значениях х ), то все его коэффициенты равны нулю
(при всех значениях х)
Если два многочлена P ( x ) и Q ( x ) тождественно равны (т.е. принимают одинаковые значения при всех значениях х ), то они совпадают (т.е. их степени одинаковы и коэффициенты при одинаковых степенях равны )
Деление многочлена на многочлен
Деление многочлена на многочлен с остатком
В случае, когда степень делимого А(х) меньше степени делителя B ( x ), считают, что неполное частное Q ( x )=0 и остаток R ( x )= A ( x )
Деление многочлена на многочлен «уголком»
Правило деления многочленов от одной переменной
Разделить многочлен на многочлен
Разместить члены многочленов по убывающим степеням переменной.
Разделить старший член делимого на старший член делителя.
Полученный резкльтат умножить на делитель и это произведение вычесть из делимого.
С полученной разностью проделывают аналогичную операцию: делят ее старший член на старший член делителя и полученный результат снова умножают на делитель и т.д. Этот процесс продолжают до тех пор, пока не получают в остатке нуль (если один многочлен делится на другой) или пока в остатке не получат многочлен, степень которого меньше степени делителя
Результат деления можно записать так:
Пример. Остаток от деления многочлена на двучлен
равен т.е. P ( x ) делится на без остатка.
(т.е. является корнем уравнения )
Простейшие свойства корней
Многочлен степени n может иметь не более n корней
Пример. Для многочлена
При n =2 для квадратного трехчлена
При n =3 для кубического многочлена имеем
Как и для квадратного трехчлена, для произвольного многочлена справедливо
Если для чисел выполняются соотношения (1),
то эти числа являются корнями многочленами
(т.е. корнями уравнения )
Пусть задан многочлен
Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена
Пример. Решить уравнение
Решение. Пробуем найти целые корни среди делителей свободного члена (-4), т.е. среди чисел ±1, ± 2, ±4. Последовательно подставляя эти числа в уравнения, находим, что x =2 – корень уравнения
Тогда многочлен делится без остатка на
Выполнив деление, получаем
и подставляем это выражение в исходное уравнение. Имеем
Рациональные корни многочлена с целыми коэффициентами
Пусть задан многочлен (или уравнение ) ()
Для любого рационального корня
Если коэффициент при старшем члене уравнения с целыми коэффициентами равен единице, то все рациональные корни этого уравнения (если они существуют) – целые числа
Пример. Решить уравнение
Выволнив деление, получаем
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-179367
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Для школьников к 1 сентября разработают короткие экскурсионные маршруты
Время чтения: 1 минута
Утверждены сроки заключительного этапа ВОШ
Время чтения: 1 минута
Во Франции планируют ввести уголовное наказание за буллинг в школе
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Москве новогодние утренники в школах и детсадах пройдут без родителей
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Заполните таблицу считая что fx и gx многочлены
Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x 4 +5x 3 +x 2 −11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу:
Следующую ячейку заполним по такому принципу: 1 ⋅ 5 + 5 = 10 :
Аналогично заполним и четвертую ячейку второй строки: 1 ⋅ 10 + 1 = 11 :
Для пятой ячейки получим: 1 ⋅ 11 + 0 = 11 :
И, наконец, для последней, шестой ячейки, имеем: 1 ⋅ 11 + ( −11) = 0 :
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x 4 +5x 3 +x 2 −11 на x−1. Естественно, что так как степень исходного многочлена 5x 4 +5x 3 +x 2 −11 равнялась четырём, то степень полученного многочлена 5x 3 +10x 2 +11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x 4 +5x 3 +x 2 −11 на x−1.
В нашем случае остаток равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю.
Можно сформулировать вывод и в такой форме: так как значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю, то единица является корнем многочлена 5x 4 +5x 3 +x 2 −11.
2. Найдите неполное частное, остаток от деления многочлена
Тема урока “Теорема Безу. Схема Горнера и ее применение”
Презентация к уроку
Тип урока: Урок усвоения и закрепления первичных знаний.
1. Организационный момент.
Сообщить тему урока, сформулировать цели.
2. Проверка домашнего задания.
3. Изучение нового материала.
Пусть Fn(x)= a n xn +a n-1x n-1 +. + a1x +a0 –многочлен относительно x степени n, где a0, a1. an –данные числа, причем a0 не равно 0. Если многочлен Fn(x) разделить с остатком на двучлен x-a, то частное (неполное частное) есть многочлен Qn-1(x) степени n-1, остаток R есть число, при этом справедливо равенство Fn(x)=(x-a) Qn-1(x) +R. Многочлен Fn(x) делится нацело на двучлен (x-a) только в случае R=0.
Теорема Безу: Остаток R от деления многочлена Fn(x) на двучлен (x-a) равен значению многочлена Fn(x) при x=a, т.е. R= Pn(a).
Немного истории. Теорема Безу, несмотря на внешнюю простоту и очевидность, является одной из фундаментальных теорем теории многочленов. В этой теореме алгебраические свойства многочленов (которые позволяют работать с многочленами как с целыми числами) связываются с их функциональными свойствами (которые позволяют рассматривать многочлены как функции). Одним из способов решения уравнений высших степеней является способ разложения на множители многочлена, стоящего в левой части уравнения. Вычисление коэффициентов многочлена и остатка записывается в виде таблицы, которая называется схемой Горнера.
Схема Горнера – это алгоритм деления многочленов, записанный для частного случая, когда частное равно двучлену x–a.
Вывод общей формулы для схемы Горнера.
Разделить с остатком многочлен f(x) на двучлен (x-c) значит найти такой многочлен q(x) и такое число r, что f(x)=(x-c)q(x)+r
Запишем это равенство подробно:
Приравняем коэффициенты при одинаковых степенях:
Демонстрация схемы Горнера на примере.
Разложение многочлена по степеням двучлена.
Любой многочлен Fn(x) степени n 
Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена.
Если старший коэффициент уравнения равен 1, то все рациональные корни уравнения, если они существуют, целые.
Закрепление изученного материала.
Для закрепления нового материала учащимся предлагается выполнить номера из учебника 2.41 и 2.42 (стр. 65).
(2 ученика решают у доски, а остальные, решив, в тетради задания сверяются с ответами на доске).
Подведение итогов.
Поняв структуру и принцип действия схемы Горнера, ее можно использовать и на уроках информатики, когда рассматривается вопрос о переводе целых чисел из десятичной системы счисления в двоичную и обратно. В основе перевода из одной системы счисления в другую лежит следующая общая теорема
Теорема. Для перевода целого числа Ap из p-ичной системы счисления в систему счисления с основанием d необходимо Ap последовательно делить с остатком на число d, записанное в той же p-ичной системе, до тех пор, пока полученное частное не станет равным нулю. Остатки от деления при этом будут являться d-ичными цифрами числа Ad, начиная от младшего разряда к старшему. Все действия необходимо проводить в p-ичной системе счисления. Для человека данное правило удобно лишь при p = 10, т.е. при переводе из десятичной системы. Что касается компьютера, то ему, напротив, “удобнее” производить вычисления в двоичной системе. Поэтому для перевода “2 в 10” используется последовательное деление на десять в двоичной системе, а “10 в 2” — сложение степеней десятки. Для оптимизации вычислений процедуры “10 в 2” компьютер использует экономную вычислительную схему Горнера. [1]
Домашнее задание. Предлагается выполнить два задание.