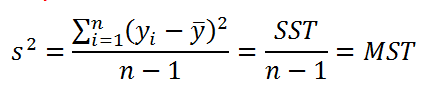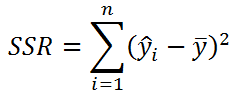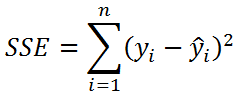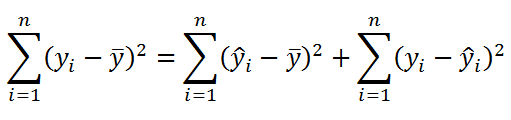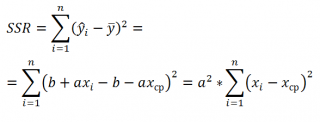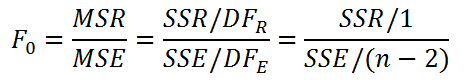Значимость f в регрессии excel что значит
Пакет анализа Excel (Регрессия)
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k объясняющих переменных) по данным примера 3.5.
| Вывод итогов | |
| Регрессионная статистика | |
| Множественный R | 0,940 |
| R-квадрат | 0,884 |
| Нормированный R – квадрат | 0,868 |
| Стандартная ошибка | 22,87 |
| Наблюдения |
В таблице регрессионной статистики приводятся значения:
Множественный R – коэффициент множественной корреляции 
R–квадрат – коэффициент детерминации R 2 ;
Нормированный R–квадрат – скорректированный R 2 с поправкой на число степеней свободы;
Стандартная ошибка– стандартная ошибка регрессии S;
Наблюдения –число наблюдений n.
| Дисперсионный анализ | ||||
| df | SS | MS | F | Значимость F |
| Регрессия | 28102,2 | 28102,2 | 53,69 | 0,00016 |
| Остаток | 3663,7 | 523,3 | ||
| Итого |
В таблице Дисперсионный анализприведены:
для строки Регрессия df = k;
для строкиОстатокdf = n – k – 1;
для строкиИтогоdf = n – 1.
2. Столбец SS –сумма квадратов отклонений, равная
для строки Регрессия 

для строкиОстаток 
для строкиИтого 
3. Столбец MSдисперсии, определяемые по формуле MS = SS/df:
для строки Регрессия – факторная дисперсия;
для строкиОстаток– остаточная дисперсия.
4. Столбец F – расчетное значение F-критерия, вычисляемое по формуле
5. Столбец Значимость F –значение уровня значимости, соответствующее вычисленной F-статистике.
Значимость F = FРАСП(F-статистика, df(регрессия), df(остаток)).
Если значимость F 2 статистически значим.
| Коэффи-циенты | Стандартная ошибка | t-cта-тистика | P-значение | Нижние 95% | Верхние 95% | |
| Y | 65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X | 0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты– значения коэффициентов a, b.
2. Стандартная ошибка–стандартные ошибки коэффициентов регрессии Sa, Sb.
3. t-статистика – расчетные значения t-критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р-значение (значимость t)– это значение уровня значимости, соответствующее вычисленной t-статистике.
Р-значение = СТЬЮДРАСП(t-статистика, df(остаток)).
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное y | Остатки e |
| 72,70 | -29,70 | |
| 82,91 | -20,91 | |
| 94,53 | -4,53 | |
| 105,72 | 5,27 | |
| 117,56 | 12,44 | |
| 129,70 | 19,29 | |
| 144,22 | 20,77 | |
| 166,49 | 24,50 | |
| 268,13 | -27,13 |
В таблице ВЫВОД ОСТАТКАуказаны:
в столбце Наблюдение– номер наблюдения;
в столбце Предсказанное y– расчетные значения зависимой переменной;
в столбце Остатки e– разница между наблюдаемыми и расчетными значениями зависимой переменной.
Пример 3.6.Имеются данные (усл. ед.) о расходах на питание y и душевого дохода x для девяти групп семей:
Используя результаты работы пакета анализа Excel (Регрессия), проанализируем зависимость расходов на питание от величины душевого дохода.
Результаты регрессионного анализа принято записывать в виде:
где в скобках указаны стандартные ошибки коэффициентов регрессии.
Коэффициенты регрессии а = 65,92 и b = 0,107. Направление связи между y и xопределяет знак коэффициентарегрессии b = 0,107, т.е. связь является прямой и положительной. Коэффициент b = 0,107 показывает, что при увеличении душевого дохода на 1 усл. ед. расходы на питание увеличиваются на 0,107 усл. ед.
Оценим значимость коэффициентов полученной модели. Значимость коэффициентов (a, b) проверяется по t-тесту:
Р-значение (a) = 0,00080
Величина R 2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R 2 проверяется по F-тесту: значимость F = 0,00016 2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как 
Проверка значимости регрессии с помощью дисперсионного анализа (F-тест)
history 26 января 2019 г.
Проведем проверку значимости простой линейной регрессии с помощью процедуры F -тест.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
F -тест для проверки значимости регрессии НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения F -теста требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
Можно, конечно, рассмотреть F -тест формально:
Определения, необходимые для F -теста
В формуле используется ряд сокращений:
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов дисперсионного анализа в различных прикладных статистических программах (в том числе и в надстройке Пакет анализа, инструмент Регрессия ).
Значение SST, характеризующую общую изменчивость переменной Y, можно разбить на 2 компоненты:
Примечание: Очевидность наличия только одной степени свободы проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы величины SSR имеет специальное обозначение: DFR (для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1) . По аналогии с MST, отношение этих величин также часто обозначают MSR = SSR / DFR .
Отношение этих величин также часто обозначают MSE = SSE / DFE .
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Число степеней свободы обладает свойством аддитивности: DFT = DFR + DFE . В этом можно убедиться, составив соответствующее равенство n -1=1+( n -2)
Процедура F -теста
Примечание : Чтобы быстрее разобраться с процедурой F -теста рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х нормальных распределений (т.е. двухвыборочный F-тест для дисперсий ).
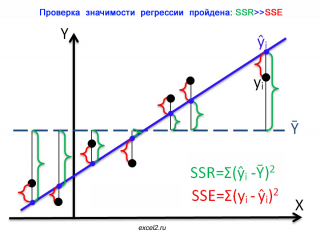
Чтобы пояснить вышесказанное изобразим на диаграммах рассеяния 2 случая:
На первой диаграмме показан случай, когда регрессия значима:
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
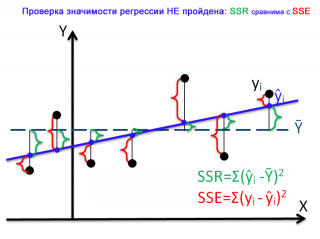
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
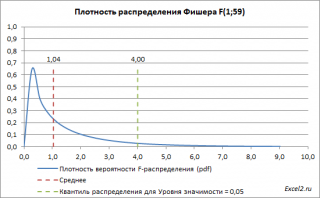
Ниже приведен график плотности вероятности F-распределения со степенями свободы 1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Значение статистики F0 может быть вычислено на основании выборки:
Вычисления в MS EXCEL
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
Значимость f в регрессии excel что значит
Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
Рис.1. Окно «Регрессия»
В появившемся диалоговом окне (рис.1) задать:
Входной интервал Y– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х– диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль– флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности– уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист– поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.
Рассмотрим результаты регрессионного анализа (рис. 2, 3).
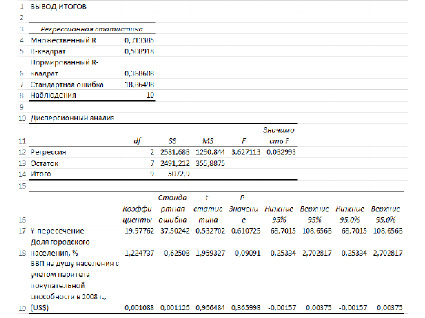
Рис. 2. Вывод итогов регрессионного анализа
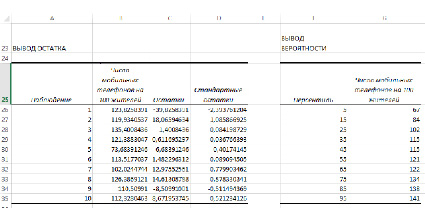
Рис. 3. Вывод остатков и вероятности по результатам регрессионного анализа
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат 0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
Остатки – остатки по модели регрессии.
На основе данных об остатках модели регрессии был построен график остатков (рис. 4) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис.5).
Рис. 4. График остатков по значениям признака «Доля городского населения, %»
Рис. 5. График подбора для признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что, возможно, качество модели можно усовершенствовать, исключив данные по Белоруссии как аномальные значения.
Значимость f в регрессии excel что значит
Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
Рис.1. Окно «Регрессия»
В появившемся диалоговом окне (рис.1) задать:
Входной интервал Y– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х– диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль– флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности– уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист– поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.
Рассмотрим результаты регрессионного анализа (рис. 2, 3).
Рис. 2. Вывод итогов регрессионного анализа
Рис. 3. Вывод остатков и вероятности по результатам регрессионного анализа
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат 0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
Предсказанное Y — теоретические (расчетные) значения результативного признака.
Остатки – остатки по модели регрессии.
На основе данных об остатках модели регрессии был построен график остатков (рис. 4) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис.5).
Рис. 4. График остатков по значениям признака «Доля городского населения, %»
Рис. 5. График подбора для признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что, возможно, качество модели можно усовершенствовать, исключив данные по Белоруссии как аномальные значения.
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k объясняющих переменных) по данным примера 3.6.
| Вывод итогов | |
| Регрессионная статистика | |
| Множественный R | 0,940 |
| R-квадрат | 0,884 |
| Нормированный R – квадрат | 0,868 |
| Стандартная ошибка | 22,87 |
| Наблюдения |
В таблице регрессионной статистики приводятся значения:
Множественный R – коэффициент множественной корреляции 
R—квадрат – коэффициент детерминации R 2 ;
Нормированный R—квадрат – скорректированный R 2 с поправкой на число степеней свободы;
Стандартная ошибка– стандартная ошибка регрессии S;
Наблюдения –число наблюдений n.
| Дисперсионный анализ | ||||
| df | SS | MS | F | Значимость F |
| Регрессия | 28102,2 | 28102,2 | 53,69 | 0,00016 |
| Остаток | 3663,7 | 523,3 | ||
| Итого |
В таблице Дисперсионный анализприведены:
1. Столбец df — число степеней свободы, равное
для строки Регрессия df = k;
для строкиОстатокdf = n – k – 1;
для строкиИтогоdf = n – 1.
2. Столбец SS –сумма квадратов отклонений, равная
для строки Регрессия 
для строкиОстаток 
для строкиИтого 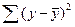
3. Столбец MSдисперсии, определяемые по формуле MS = SS/df:
для строки Регрессия – факторная дисперсия;
для строкиОстаток– остаточная дисперсия.
4. Столбец F – расчетное значение F-критерия, вычисляемое по формуле
5. Столбец Значимость F –значение уровня значимости, соответствующее вычисленной F-статистике.
Значимость F = FРАСП(F-статистика, df(регрессия), df(остаток)).
Если значимость F 2 статистически значим.
| Коэффи-циенты | Стандартная ошибка | t-cта-тистика | P-значение | Нижние 95% | Верхние 95% | |
| Y | 65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X | 0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты– значения коэффициентов a, b.
2. Стандартная ошибка–стандартные ошибки коэффициентов регрессии Sa, Sb.
3. t-статистика – расчетные значения t-критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р-значение (значимость t)– это значение уровня значимости, соответствующее вычисленной t-статистике.
Р-значение = СТЬЮДРАСП(t-статистика, df(остаток)).
Величина R 2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R 2 проверяется по F-тесту: значимость F = 0,00016 2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как 
Процедура «Регрессия» пакета «Анализ данных»
Процедура решает простейшую задачу парной линейной регрессии:
– по заданным значениям 

– вычисляет некоторые статистики для анализа качества аппроксимации.
Исходные данные для функции
— выборочные значения 
Содержание отчёта о вычислениях, которые выполняются процедурой, определяется пользователем.
Основные численные результаты представлены в трёх таблицах под общим заголовком
R-квадрат – коэффициент детерминации: 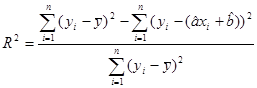
Стандартная ошибка — стандартная ошибка регрессии: 

В двух строках таблицы отображаются статистики, относящиеся соответственно к регрессии и к остаткам регрессии:
df — число степеней свободы: 
SS — сумма квадратов регрессии: 
F — значение критерия Фишера: 
Следующая таблица — основная таблица, описывающая линию регрессии.
В двух строках таблицы отображаются статистики, относящиеся соответственно к константе b (Y-пересечение) и к коэффициенту a (Переменная X 1) в уравнении линии регрессии y = ax + b :
Коэффициенты — значения коэффициентов соответственно b и a в уравнении линии регрессии y = ax + b ;
Стандартная ошибка — стандартная ошибка регрессии: 

t-статистика — вычисленное по выборке значение критерия Стьюдента для проверки значимости коэффициентов (нулевая гипотеза – коэффициент равен нулю): точечная оценка коэффициента, делённая на его стандартную ошибку: 
Нижние 95%, Верхние 95%, Нижние 90.0%, Верхние 90.0% — соответственно нижние и верхние границы доверительных интервалов для коэффициентов b и a (границы вычисляются с 95% доверительной вероятностью вычисляются по умолчанию, и с p %, заданной пользователем).
На приведенном ниже рисунке можно видеть решение задачи для различных типов аппроксимирующих функций.