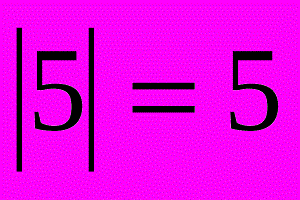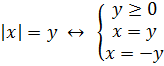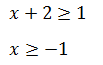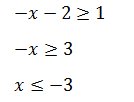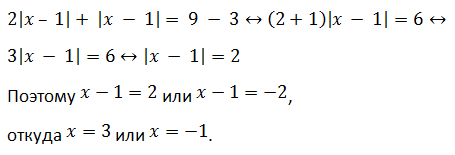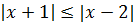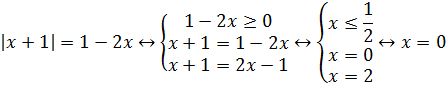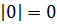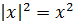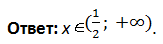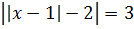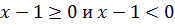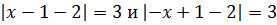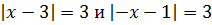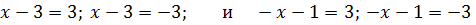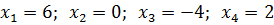Знак двойного модуля что означает

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

Модуль комплексного числа

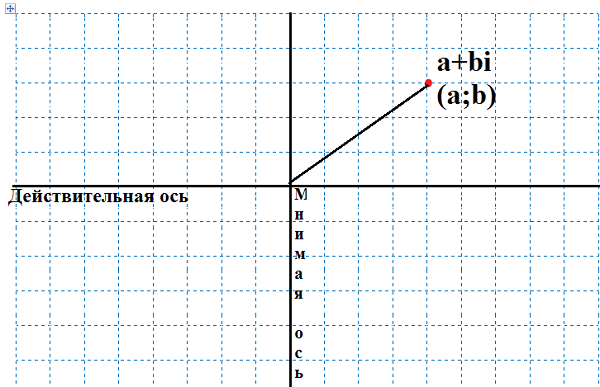
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Ответ: x = 0.

Модуль суммы

Модуль разности

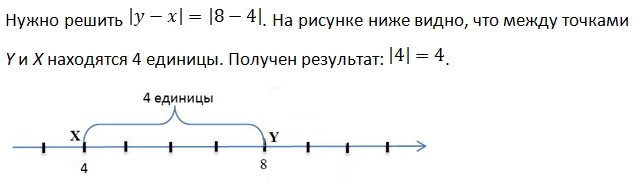
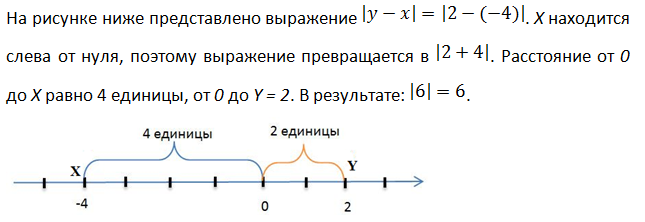
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

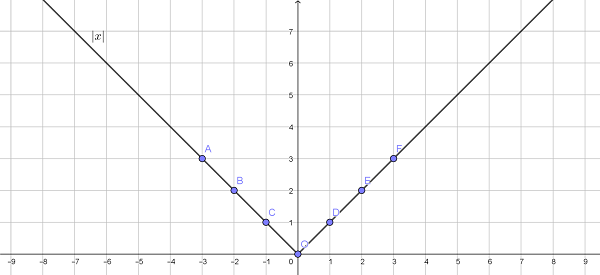
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

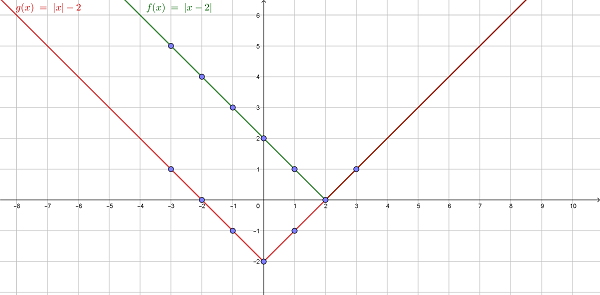
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Источник

Модуль числа — теория и решение задач

Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂

А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.

Ситуация первая

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?

Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.

Ситуация третья

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее…

Источник

Решение неравенств с модулем

Сегодня, друзья, не будет никаких соплей и сантиментов. Вместо них я без лишних вопросов отправлю вас в бой с одним из самых грозных противников в курсе алгебры 8—9 класса.

Да, вы всё правильно поняли: речь идёт о неравенствах с модулем. Мы рассмотрим четыре основных приёма, с помощью которых вы научитесь решать порядка 90% таких задач. А что с остальными 10%? Что ж, о них мы поговорим в отдельном уроке.:)

Однако перед тем, как разбирать какие-то там приёмы, хотелось бы напомнить два факта, которые уже необходимо знать. Иначе вы рискуете вообще не понять материал сегодняшнего урока.

Что уже нужно знать

Капитан Очевидность как бы намекает, что для решения неравенств с модулем необходимо знать две вещи:

Начнём со второго пункта.

Определение модуля

Тут всё просто. Есть два определения: алгебраическое и графическое. Для начала — алгебраическое:

Записывается это так:

Говоря простым языком, модуль — это «число без минуса». И именно в этой двойственности (где-то с исходным числом ничего не надо делать, а где-то придётся убрать какой-то там минус) и заключается вся сложность для начинающих учеников.

Есть ещё геометрическое определение. Его тоже полезно знать, но обращаться к нему мы будем лишь в сложных и каких-то специальных случаях, где геометрический подход удобнее алгебраического (спойлер: не сегодня).

Если начертить картинку, то получится что-то типа этого:

Графическое определение модуля

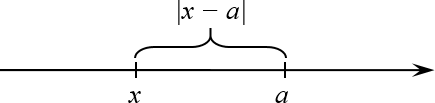
Так или иначе, из определения модуля сразу следует его ключевое свойство: модуль числа всегда является величиной неотрицательной. Этот факт будет красной нитью идти через всё наше сегодняшнее повествование.

Решение неравенств. Метод интервалов

Теперь разберёмся с неравенствами. Их существует великое множество, но наша задача сейчас — уметь решать хотя бы самые простые из них. Те, которые сводятся к линейным неравенствам, а также к методу интервалов.

На эту тему у меня есть два больших урока (между прочем, очень, ОЧЕНЬ полезных — рекомендую изучить):

Если вы всё это знаете, если фраза «перейдём от неравенства к уравнению» не вызывает у вас смутное желание убиться об стену, то вы готовы: добро пожаловать в ад к основной теме урока.:)

1. Неравенства вида «Модуль меньше функции»

Это одна из самых часто встречающихся задач с модулями. Требуется решить неравенство вида:

Все они решаются буквально в одну строчку по схеме:

Естественно, возникает вопрос: а проще нельзя? К сожалению, нельзя. В этом вся фишка модуля.

Впрочем, хватит философствовать. Давайте решим парочку задач:

\[\left| 2x+3 \right| \lt x+7\]

Решение. Итак, перед нами классическое неравенство вида «модуль меньше» — даже преобразовывать нечего. Работаем по алгоритму:

Не торопитесь раскрывать скобки, перед которыми стоит «минус»: вполне возможно, что из-за спешки вы допустите обидную ошибку.

Поскольку дальше нужно решить каждое неравенство отдельно, пора переходить к системе (можно было сделать это и раньше, но тогда решение получится чуть более громоздким):

Задача свелась к двум элементарным неравенствам. Отметим их решения на параллельных числовых прямых:

Пересечение множеств

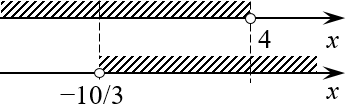
Пересечением этих множеств и будет ответ.

Задача. Решите неравенство:

\[\left| <^<2>>+2x-3 \right|+3\left( x+1 \right) \lt 0\]

Решение. Это задание уже чуть посложнее. Для начала уединим модуль, перенеся второе слагаемое вправо:

Очевидно, перед нами вновь неравенство вида «модуль меньше», поэтому избавляемся от модуля по уже известному алгоритму:

А мы для начала просто избавимся от двойного минуса слева:

Теперь раскроем все скобки в двойном неравенстве:

Переходим к двойному неравенству. В этот раз выкладки будут посерьёзнее:

Оба неравенства являются квадратными и решаются методом интервалов (потому и говорю: если не знаете, что это такое, лучше пока не браться за модули). Переходим к уравнению в первом неравенстве:

Как видим, на выходе получилось неполное квадратное уравнение, которое решается элементарно. Теперь разберёмся со вторым неравенством системы. Там придётся применить теорему Виета:

Отмечаем полученные числа на двух параллельных прямых (отдельная для первого неравенства и отдельная для второго):

Думаю, после этих примеров схема решения предельно ясна:

Аналогичный алгоритм существует и для неравенств следующего типа, когда модуль больше функции. Однако там есть парочка серьёзных «но». Об этих «но» мы сейчас и поговорим.

2. Неравенства вида «Модуль больше функции»

Похоже на предыдущее? Похоже. И тем не менее решаются такие задачи совсем по-другому. Формально схема следующая:

Другими словами, мы рассматриваем два случая:

При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Обратите внимание ещё раз: перед нами не система, а совокупность, поэтому в ответе множества объединяются, а не пересекаются. Это принципиальное отличие от предыдущего пункта!

Вообще, с объединениями и пересечениями у многих учеников сплошная путаница, поэтому давайте разберёмся в этом вопросе раз и навсегда:

Чтобы ещё проще было запомнить, просто пририсуйте к этим знакам ножки, чтобы получились бокалы (вот только не надо сейчас обвинять меня в пропаганде наркомании и алкоголизма: если вы всерьёз изучаете этот урок, то вы уже наркоман):

Разница между пересечением и объединением множеств

В переводе на русский это означает следующее: объединение (совокупность) включает в себя элементы из обоих множеств, поэтому никак не меньше каждого из них; а вот пересечение (система) включает в себя лишь те элементы, которые одновременно находятся и в первом множестве, и во втором. Поэтому пересечение множеств никогда не бывает больше множеств-исходников.

Так стало понятнее? Вот и отлично. Переходим к практике.

\[\left| 3x+1 \right| \gt 5-4x\]

Решение. Действуем по схеме:

Решаем каждое неравенство совокупности:

\[\left[ \begin & x \gt 4/7\ \\ & x \gt 6 \\ \end \right.\]

Отмечаем каждое полученное множество на числовой прямой, а затем объединяем их:

Объединение множеств

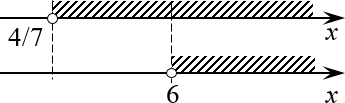
Задача. Решите неравенство:

Решение. Ну что? Да ничего — всё то же самое. Переходим от неравенства с модулем к совокупности двух неравенств:

Решаем каждое неравенство. К сожалению, корни там будут не оч:

Во втором неравенстве тоже немного дичи:

Теперь нужно отметить эти числа на двух осях — по одной оси для каждого неравенства. Однако отмечать точки нужно в правильном порядке: чем больше число, тем дальше сдвигам точку вправо.

Поэтому давайте сравнивать:

Мы уединили корень, получили неотрицательные числа с обеих сторон неравенства, поэтому вправе возвести обе стороны в квадрат:

Случай некрасивых корней

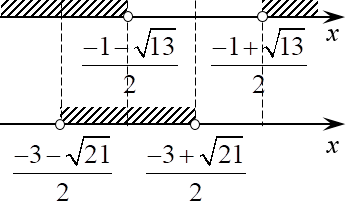
Напомню, мы решаем совокупность, поэтому в ответ пойдёт объединение, а не пересечение заштрихованных множеств.

Как видите, наша схема прекрасно работает как для простых задач, так и для весьма жёстких. Единственное «слабое место» в таком подходе — нужно грамотно сравнивать иррациональные числа (и поверьте: это не только корни). Но вопросам сравнения будет посвящён отдельный (и очень серьёзный урок). А мы идём дальше.

3. Неравенства с неотрицательными «хвостами»

Вот мы и добрались до самого интересного. Это неравенства вида:

\[\left| f \right| \gt \left| g \right|\]

Вообще говоря, алгоритм, о котором мы сейчас поговорим, верен н только для модуля. Он работает во всех неравенствах, где слева и справа стоят гарантированно неотрицательные выражения:

\[f \gt g,\quad f\ge 0,g\ge 0\]

Что делать с этими задачами? Просто помните:

В неравенствах с неотрицательными «хвостами» можно возводить обе части в любую натуральную степень. Никаких дополнительных ограничений при этом не возникнет.

Прежде всего нас будет интересовать возведение в квадрат — он сжигает модули и корни:

Вот только не надо путать это с извлечением корня из квадрата:

Бесчисленное множество ошибок было допущено в тот момент, когда ученик забывал ставить модуль! Но это совсем другая история (это как бы иррациональные уравнения), поэтому не будем сейчас в это углубляться. Давайте лучше решим парочку задач:

\[\left| x+2 \right|\ge \left| 1-2x \right|\]

Решение. Сразу заметим две вещи:

Следовательно, можем возвести обе части неравенства в квадрат, чтобы избавиться от модуля и решать задачу обычным методом интервалов:

Дальше можно перенести всё вправо и расписать разность квадратов. Только аккуратно:

Решаем методом интервалов. Переходим от неравенства к уравнению:

Отмечаем найденные корни на числовой прямой. Ещё раз: все точки закрашены, поскольку исходное неравенство — нестрогое!

Избавление от знака модуля

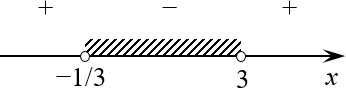
Ну вот и всё. Задача решена.

Задача. Решите неравенство:

Решение. Делаем всё то же самое. Я не буду комментировать — просто посмотрите на последовательность действий.

Возводим в квадрат:

Всего один корень на числовой прямой:

Ответ — целый интервал

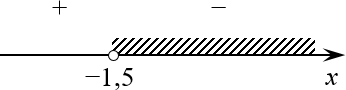
Небольшое замечание насчёт последней задачи. Как точно подметил один мой ученик, оба подмодульных выражения в данном неравенстве заведомо положительны, поэтому знак модуля можно без ущерба для здоровья опустить.

Но это уже совсем другой уровень размышлений и другой подход — его условно можно назвать методом следствий. О нём — в отдельном уроке. А сейчас перейдём к финальной части сегодняшнего урока и рассмотрим универсальный алгоритм, который работает всегда. Даже тогда, когда все предыдущие подходы оказались бессильны.:)

4. Метод перебора вариантов

А что, если все эти приёмы не помогут? Если неравенство не сводится неотрицательным хвостам, если уединить модуль не получается, если вообще боль-печаль-тоска?

Тогда на сцену выходит «тяжёлая артиллерия» всей математики — метод перебора. Применительно к неравенствам с модулем выглядит он так:

Ну как? Слабо? Легко! Только долго. Посмотрим на практике:

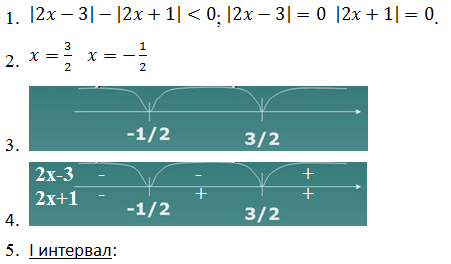
\[\left| x+2 \right| \lt \left| x-1 \right|+x-\frac<3><2>\]

Выписываем подмодульные выражения, приравниваем их к нулю и находим корни:

Итого у нас два корня, которые разбивают числовую прямую на три участка, внутри которых каждый модуль раскрывается однозначно:

Разбиение числовой прямой нулями подмодульных функций

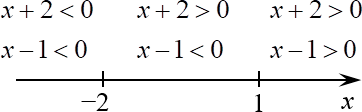
Рассмотрим каждый участок отдельно.

Снова пересекаем с исходным требованием:

И снова пустое множество решений, поскольку нет таких чисел, которые одновременно меньше −2,5, но больше −2.

\[\begin & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\\end\]

И вновь пересекаем найденное множество с исходным ограничением:

Ну наконец-то! Мы нашли интервал, который и будет ответом.

Напоследок — одно замечание, которое, возможно, убережёт вас от глупых ошибок при решении реальных задач:

Решения неравенств с модулями обычно представляют собой сплошные множества на числовой прямой — интервалы и отрезки. Гораздо реже встречаются изолированные точки. И ещё реже случается так, что границ решения (конец отрезка) совпадает с границей рассматриваемого диапазона.

Следовательно, если границы (те самые «частные случаи») не входят в ответ, то почти наверняка не войдут в ответ и области слева-справа от этих границ. И напротив: граница вошла в ответ — значит, и какие-то области вокруг неё тоже будут ответами.

Помните об этом, когда проверяете свои решения.

Источник