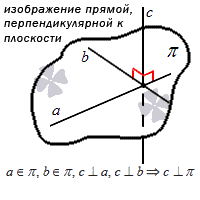
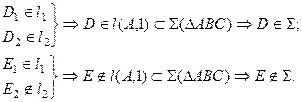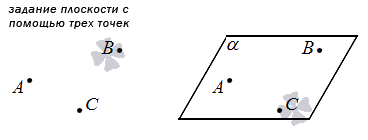Знак того что точка лежит в плоскости

Предмет стереометрии. Аксиомы стереометрии

Стереометрия – это раздел геометрии, в котором изучают свойства фигур в пространстве. Слово “стереометрия” происходит от греческих слов “стереос” – объёмный, пространственный и “метрео” – измерять.

Самыми простыми и основными фигурами в пространстве являются точки, прямые и плоскости. Наряду с этими фигурами рассматривают геометрические тела и их поверхности. Представление о геометрических телах дают окружающие нас предметы. Поверхности тел составленные из многоугольников называются многогранниками. Одним из простейших многогранников является куб (кубик рубик имеет форму куба). Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром. Такую же форму имеет футбольный мяч. Консервная банка имеет форму геометрического тела, называемого цилиндром.

В отличии от реальных предметов геометрические тела, ка и всякие геометрические фигуры, являются воображаемыми объектами. Мы представляем геометрическое тело как часть пространства, определённую от остальной части пространства поверхностью – границей этого тела. Граница шара есть сфера, а граница цилиндра состоит из двух кругов – оснований цилиндра и боковой поверхности.

Изучая свойства геометрических фигур – воображаемых объектов, мы получаем представление о геометрических свойствах реальных предметов (их формы, взаимное расположение и так далее) и можем применять эти свойства на практике.

При изучении планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается ещё одна основная фигура – плоскость. Представление о плоскости даёт гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе как простирающийся неограниченно во все стороны.

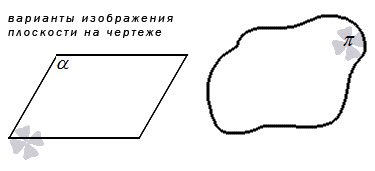
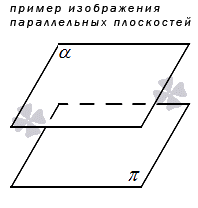
Плоскости обозначатся греческими буквами α, β, γ и так далее. На рисунках плоскости обозначаются в виде параллелограмма или в виде произвольной области

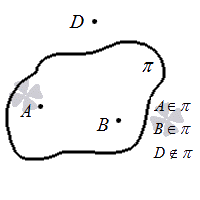
Понятно, что в каждой плоскости лежат какие-то точки пространства, но не все точки пространства лежат в одной и той же плоскости.

Источник

Точка и прямая

Точка и прямая являются основными геометрическими фигурами на плоскости.

Определение точки и прямой в геометрии не вводят, эти понятия рассматриваются на интуитивно-понятийном уровне.

Точки обозначают прописными (заглавными, большими) латинскими буквами: A, B, C, D, …

Прямые обозначают одной строчной (маленькой) латинской буквой, например,

Прямая состоит из бесконечного множества точек и не имеет ни начала, ни конца. На рисунке изображают только часть прямой, но понимают, что она простирается в пространстве бесконечно далеко, неограниченно продолжаясь в обе стороны.

О точках, которые лежат на прямой, говорят, что они принадлежат этой прямой. Принадлежность отмечают знаком ∈. О точках вне прямой говорят, что они не принадлежат этой прямой. Знак «не принадлежит» — ∉.

Например, точка B принадлежит прямой a (пишут: B∈a),

точка F не принадлежит прямой a, (пишут: F∉a).

Основные свойства принадлежности точек и прямых на плоскости:

Каковы бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и притом только одну.

Прямые также обозначают двумя большими латинскими буквами, по названию точек, которые лежат на прямой.

— эту прямую можно назвать MK или MN или NK.

Две прямые могут пересекаться и не пересекаться. Если прямые не пересекаются, они не имеют общих точек. Если прямые пересекаются, они имеют одну общую точку. Знак пересечения — ∩.

Например, прямые a и b пересекаются в точке O

(пишут: a ∩ b=O).

Прямые c и d также пересекающиеся, хотя на рисунке нет их точки пересечения.

Прямые m и n не имеют общих точек.

Источник

Как доказать что точка принадлежит плоскости

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими ‘ положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное множество линий. Это могут быть произвольные линии и линии, занимающие особое положение по отношению к плоскостям проекций П₁ П₂, П₃.Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно горизонтальной плоскости проекций, называется горизонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рис. 5.8).

К линии уровня относится и профильная прямая, лежащая в заданной плоскости и параллельная П₃.

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклонаплоскости к плоскости проекций.

Определение угла наклона плоскости

К плоскостям проекций

Плоскость общего положения, расположенная в пространстве
произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо
плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П₁ – линия ската, к П₂ – линия наибольшего наклона плоскости к плоскости П₂.

Линии наибольшего наклона плоскости – это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленное данной плоскостью и плоскостью проекций (рис. 5.10).

Последнее изменение этой страницы: 2016-12-10; Нарушение авторского права страницы

Рис. 3.2 Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

.

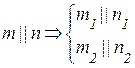
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

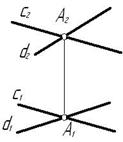
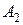
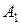
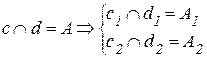
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная () и горизонтальная ()проекции этой точки должны находиться на одной линии связи.

.

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

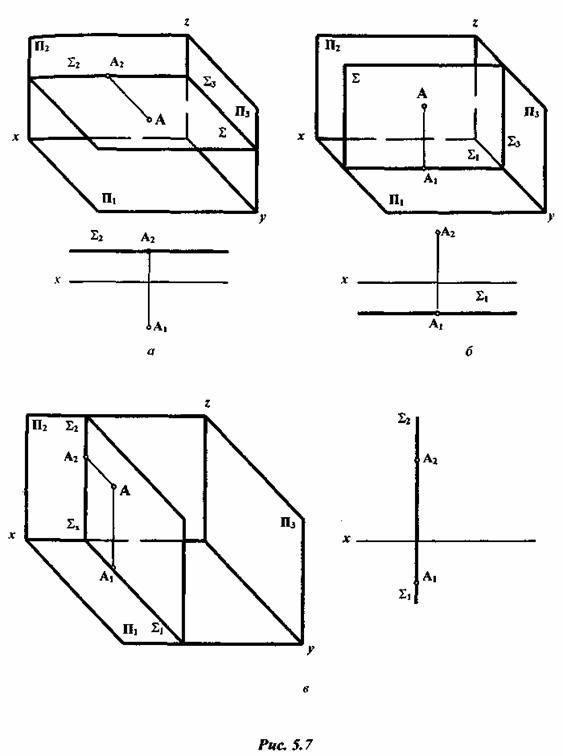
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

На рис. 3.5 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

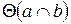
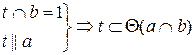
На рис. 3.6 показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – | 7538 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: – если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.

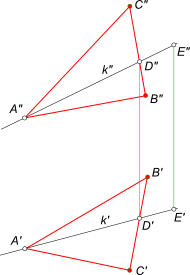
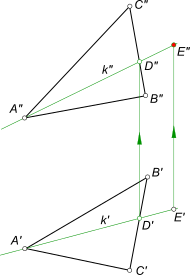
Задача на принадлежность точки плоскости может быть выражена следующим образом: – заключить точку E(E`, E”) в; – провести через точку E(E`, E”) плоскость α общего положения

Положение плоскости α в пространстве определяется тремя точками – вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки A и D принадлежат этой плоскости. Проведя прямую в плоскости через точку E

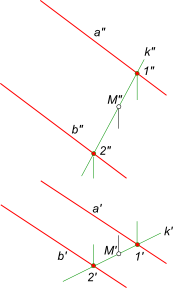
доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: – проводим прямую через точку M; – через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.

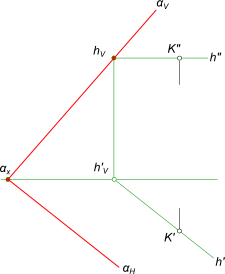
Через точку M провести плоскость α заданную следами

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: – проводим прямую h (горизонталь искомой плоскости) через точку K; – проводим горизонтальный след α_H // h` ⇒ α_x; – через точки α_x и h_V проводим фронтальный след α_V.

Источник

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Как могут располагаться плоскость и точка друг относительно друга

Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

Графически последнюю аксиому можно представить так:

Варианты взаимного расположения прямой и плоскости

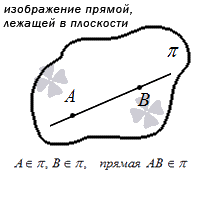
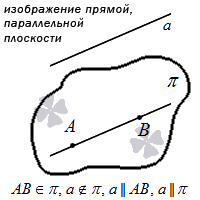
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

Графически этот вариант расположения выглядит так:

Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

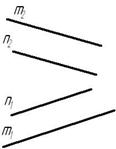
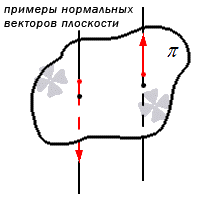
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

Примеры нормальных векторов плоскости показаны на рисунке:

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

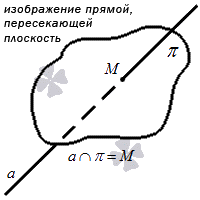
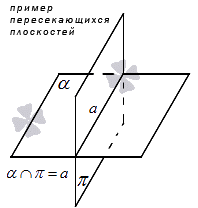
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

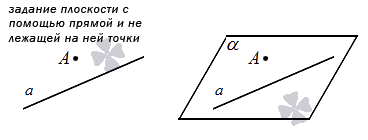
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

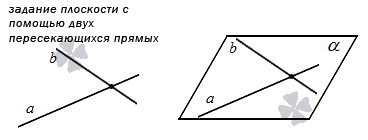
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

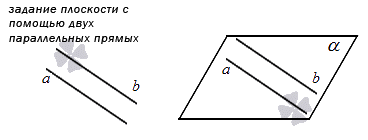
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

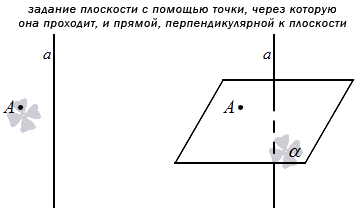
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

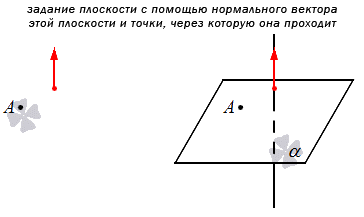
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Источник

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник