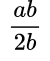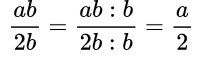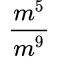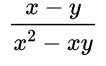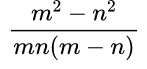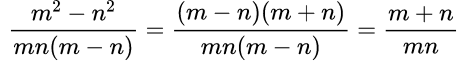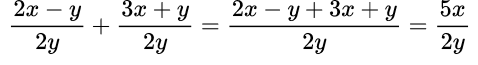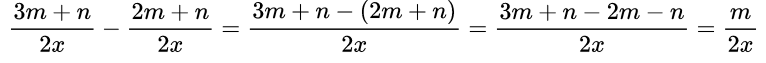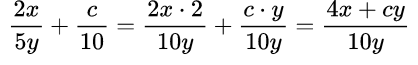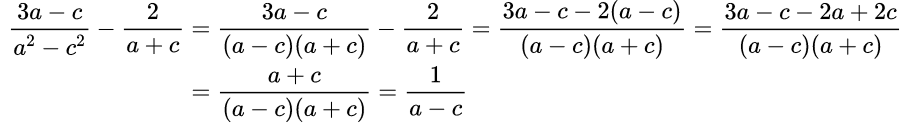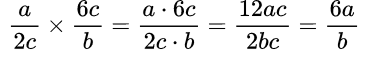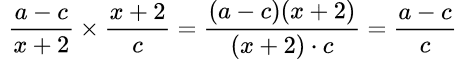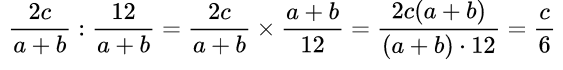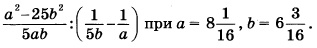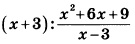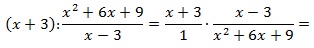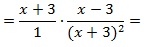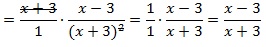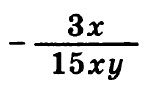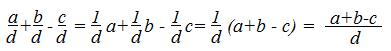Зная что найдите значение алгебраической дроби
Алгебраические дроби
теория по математике 📈 алгебраические выражения
Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.
Примеры алгебраических дробей:
Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.
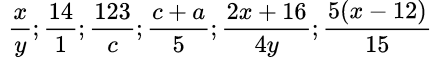
Сокращение алгебраической дроби
Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.
Пример №1. Сократим дробь: 
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь: 
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :
Пример №3. Сократим дробь: 
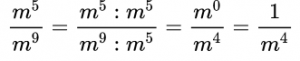
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
Пример №4. Сократим дробь: 
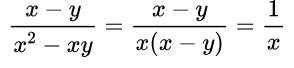
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).
Пример №5. Выполним сложение дробей: 
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей: 
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:
Пример №7. Выполнить сложение дробей: 
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей: 
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.
Пример №9. Выполнить умножение дробей:
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей: 
Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.
Пример №11. Выполнить деление дробей:
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению: 
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b): 
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): 
Подставим полученные значения в выражение и найдем конечный результат: 
Ответ: 39
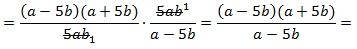
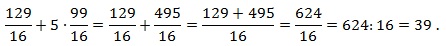
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
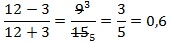
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Понятие алгебраической дроби. Основное свойство
Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
Алгоритм приведения алгебраических дробей к общему знаменателю
Шаг 2. Дополнительные множители
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
Дробь также не изменится, если провести следующие перемены знаков:
Ещё несколько полезных формул, связанных с переменой знаков:
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
$ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$
$ 3x-1 \neq 0 \iff x \neq \frac<1><3>$
$$ x- \frac<4>
$ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff <\left\< \begin
Пример 2. Сократите дроби:
Пример 3. Упростите выражение:
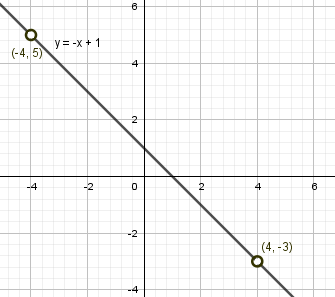
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
Алгебраические дроби.
Значение алгебраической дроби. Алгебраическая дробь – это выражение вида a/b, где a и b могут быть
числом, одночленом, многочленом. Как и в арифметике, a называется числителем, b – знаменателем.
Арифметическая дробь является частным случаем алгебраической.
Многочлен — это частный случай алгебраической дроби.
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями.
Сложение и вычитание алгебраических дробей c одинаковыми знаменателями выполняется по тому же
,
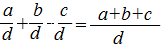
Т.e. составляют соответствующую алгебраическую сумму числителей, а знаменатель оставляют без
изменений, по сути, мы выносим общий множитель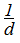 
за скобку.
Для сложения или вычитания двух или нескольких дробей любого вида (смешанные, неправильные, с
разными знаменателями …), необходимо выполнить те же самые действия, что и в арифметике.
Основное свойство алгебраической дроби.
Дробь не имеет смысла, если ее знаменатель равен нулю.
Алгебраические дроби, примеры.
,
,
.
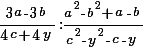
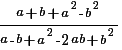
Действия с алгебраическими дробями
После полученных начальных сведений о дробях перейдем к действиям с алгебраическими дробями. С ними можно выполнять любые действия вплоть до возведения в степень. При их выполнении мы в итоге получаем алгебраическую дробь. Все пункты необходимо разбирать последовательно.
Действия с алгебраическими дробями аналогичны действиям с обыкновенными дробями. Поэтому стоит отметить, что правила являются совпадающими при любых выполняемых с ними действиями.
Сложение алгебраических дробей
Сложение может выполняться в двух случаях: при одинаковых знаменателях, при наличии разных знаменателей.
Если необходимо произвести сложение дробей с одинаковыми знаменателями, нужно сложить числители, а знаменатель оставить без изменения. Это правило позволяет воспользоваться сложением дробей и многочленов, которые находятся в числителях. Получим, что
Если имеются числители дроби с разными числителями, тогда необходимо применить правило: воспользоваться приведением к общему знаменателю, выполнить сложение полученных дробей.
Решение
Выполним сложение и получим, что
Статья о сложении и вычитании таких дробей имеет подробную информацию, где подробно описано каждое действие, производимое над дробями. При выполнении сложения возможно появление сократимой дроби.
Вычитание
Вычитание выполняется аналогично сложению. При одинаковых знаменателях действия выполняются только в числителе, знаменатель остается неизменным. При различных знаменателях выполняется приведение к общему. Только после этого можно приступать к вычислениям.
Решение
Ответ: 2
Решение
Детальная информация указана в статье о сложении и вычитании алгебраических дробей.
Умножение алгебраических дробей
С дробями можно производить умножение аналогичное умножению обыкновенных дробей: для того, чтобы умножить дроби, необходимо произвести умножение числителей и знаменателей отдельно.
Рассмотрим пример такого плана.
Теперь необходимо выполнить преобразования, то есть умножить одночлен на многочлен. Получаем, что
Предварительно следует произвести разложение дроби на многочлены для того, чтобы упростить дробь. После можно производить сокращение. Имеем, что
Подробное рассмотрение данного действия можно найти в статье умножения и деления дробей.
Деление
Рассмотрим деление с алгебраическими дробями. Применим правило: для того, чтобы разделить дроби, необходимо первую умножить на обратную вторую.
Дробь, которая обратная данной считается дробь с поменянными местами числителем и знаменателем. То есть, эта дробь называется взаимообратной.
Решение
Возведение алгебраической дроби в степень
Если имеется натуральная степень, тогда необходимо применять правило действий с возведением в натуральную степень. При таких вычислениях используем правило: при возведении в степень нужно числитель и знаменатель отдельно возводить в степени, после чего записать результат.
Детальное решение подобных примеров рассматривается в статье про возведение алгебраической дроби в степень.
При работе со степенью дроби необходимо помнить, что числитель и знаменатель отдельно возводятся в степень. Это заметно упрощает процесс решения и дальнейшего упрощения дроби. Стоит обращать внимание и на знак перед степенью. Если имеется знак «минус», то такую дробь следует переворачивать для простоты вычисления.