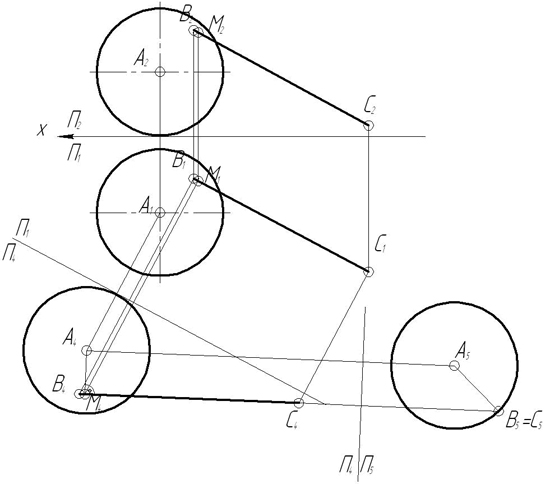
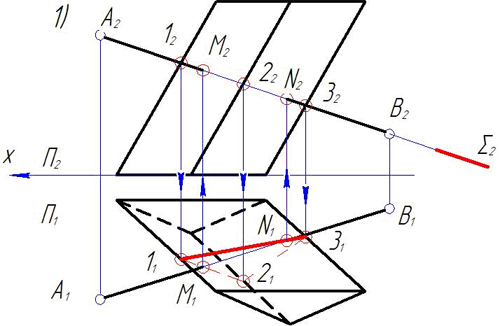
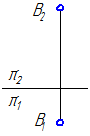Зная что точка с принадлежит отрезку ав построить недостающую проекцию точки с

Зная что точка с принадлежит отрезку ав построить недостающую проекцию точки с

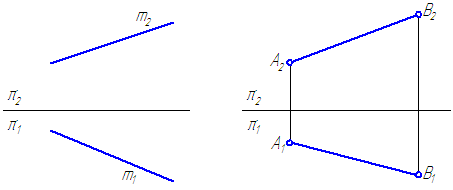
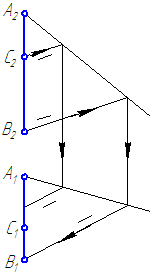
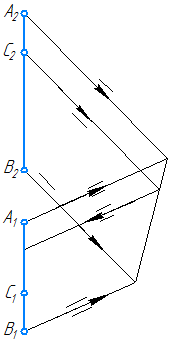
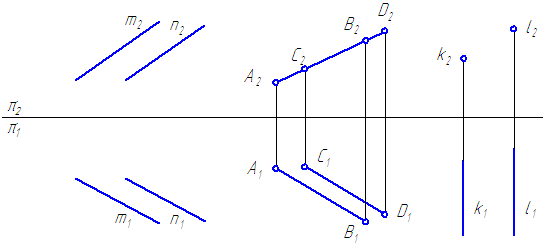
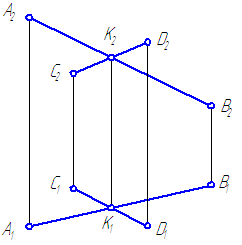
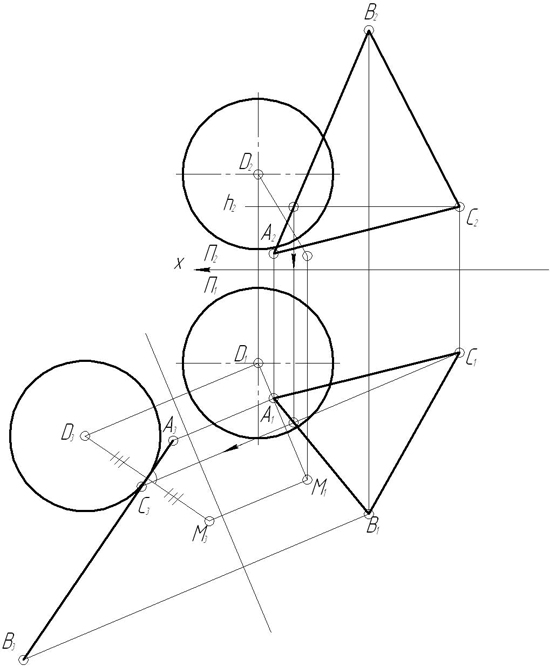
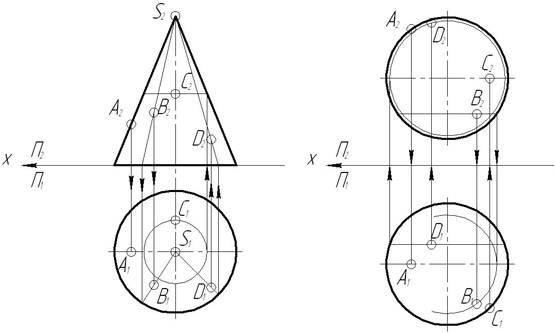
11. Зная, что точка C принадлежит отрезку AB, построить недостающую проекцию точки С.

12. На отрезке MN найти точку K, делящую отрезок в отношении MK: KN=4:1.

13. Построить проекции отрезка MN длиной 35 мм, принадлежащего произвольной горизонтали.

14. Построить проекции отрезка KL длиной 40 мм, принадлежащего произвольной фронтали.

15. Через произвольную точку А провести горизонталь под углом 30 к П₂. Сколько решений имеет задача?

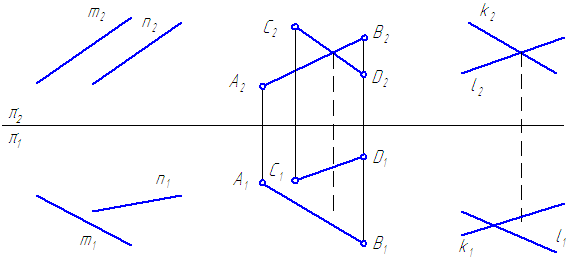
17. Определить относительное положение прямых.

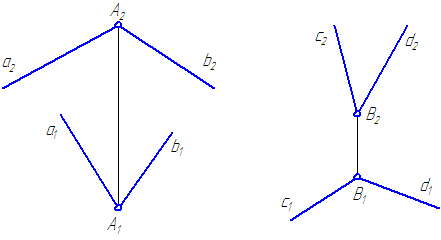
18. Через точку А провести горизонталь и фронталь, пересекающие:

прямую с общего положения;

профильную прямую p.

19. Прямые a и b пересечь горизонталью.

20. Скрещивающиеся прямые a и b пересечь фронтально-проецирующей прямой i;

прямые c и d пересечь горизонтально-проецирующей прямой g

Источник

1. Точка и прямая

Построить недостающую проекцию точки А , если известно, что точка отстоит от оси х на 30 мм.

Определить расстояние от точки А до прямой e.

Построить точку С, принадлежащую отрезку АВ и отстоящую от точки А на 25 мм.

Построить точку A, принадлежащую прямой e и отстоящую от прямой n на 20 мм.

Найти фронтальную проекцию точки С, принадлежащую отрезку АВ (профильную проекцию не строить).

По горизонтальной проекции A₁B₁ отрезка построить его фронтальную проекцию, зная натуральную величину отрезка AB.

Построить недостающую проекцию точки C, равноудаленную от точек А и B.

Через точку C провести прямую l, параллельную отрезку AB.

Построить недостающую проекцию точки А, зная, что расстояние от точки А до прямой e равно 15 мм.

Методом замены плоскостей проекций определить натуральную величину отрезка АВ и угол его наклона к плоскости проекций П₁.

Методом замены плоскостей проекций определить натуральную величину отрезка АВ и угол его наклона к плоскости проекций П₂.

Построить точку В, симметричную точке А относительно прямой m.

Источник

Лекция 2. Ортогональные проекции прямой

2.1. Задание прямой на эпюре

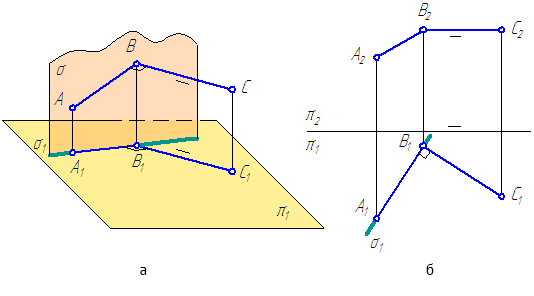
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.

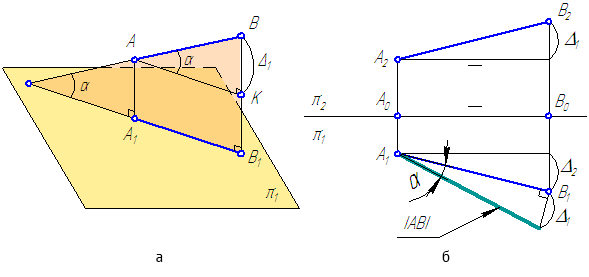
а б
Рисунок 2.1 – Проекции прямой

Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.

Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.

2.2. Прямые частного положения

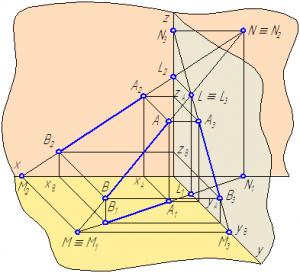
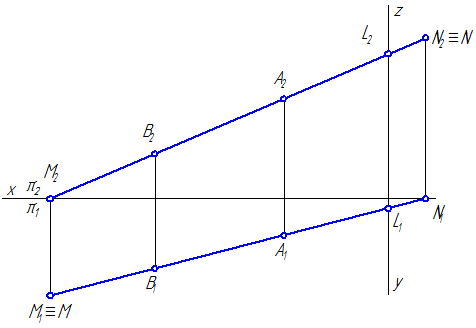
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).

Рисунок 2.2 – Эпюр горизонтали

Если отрезок параллелен плоскости проекций π₁, то его фронтальная проекция А₂В₂ параллельна оси проекций π₁/π₂, а горизонтальная проекция отрезка А₁В₁ определяет истинную величину АВ:

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).

Рисунок 2.3 – Эпюр фронтали

Если отрезок параллелен плоскости проекций π₂, то его горизонтальная проекция параллельна оси проекций π₂/π₁, а фронтальная проекция отрезка C₂D₂ определяет истинную величину CD.

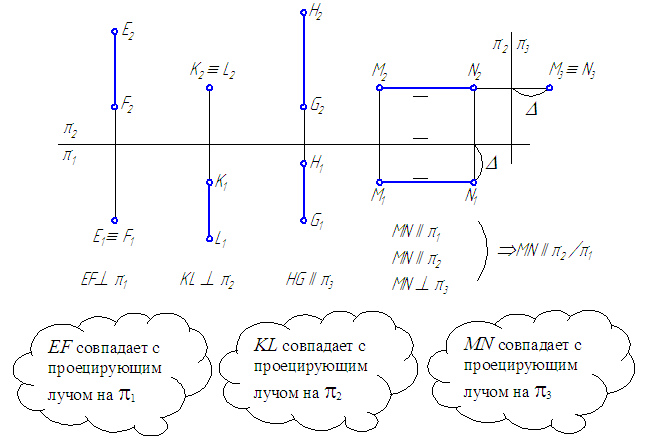
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).

Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).

Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).

Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).

Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH

2.3. Метод прямоугольного треугольника

Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.

Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π₁ (Рисунок 2.5).

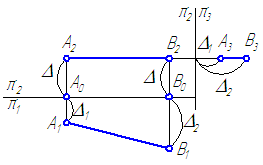
Рисунок 2.5 – Определение истинной величины отрезка общего положения

АА₁ – расстояние от точки А до плоскости проекций π₁;

ВВ₁ – расстояние от точки В до плоскости проекций π₁;

ΔАКВ – прямоугольный треугольник, в котором:

ВК=ВВ₁–АА₁=Δ₁ – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π₁ (то есть, разности координат Z точек А и В);

АВ – гипотенуза ΔАКВ – истинная величина.

При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.

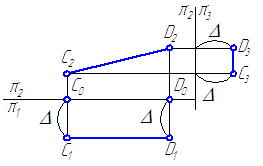
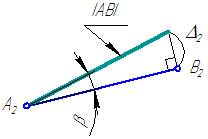
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π₂

2.4. Точка и прямая

Если точка принадлежит прямой, то её проекции:

Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:

Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:

Упражнение

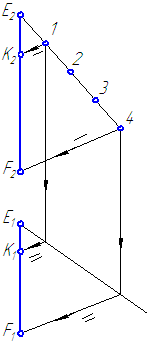
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)

Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:

Упражнение

Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).

Рисунок 2.9а – Решение упражнения 2. Способ 1.

Рисунок 2.9б – Решение упражнения 2. Способ 2.

Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.

2.5. Следы прямой

След прямой – точка пересечения прямой с плоскостью проекций.

Прямая общего положения в общем случае может быть три следа:

След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

Рисунок 2.10 – Построение следов отрезка прямой АВ

Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

Для построения горизонтального следа прямой АB необходимо:

Чтобы построить фронтальный след отрезка АB прямой, необходимо:

Ниже приводим алгоритм построения следов отрезка прямой АВ:

Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

2.6. Взаимное расположение прямых

Две прямые в пространстве могут быть:

Параллельные прямые – прямые, пересекающиеся в несобственной точке.

Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

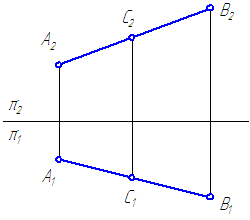
Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.

Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

Рисунок 2.13 – Пересекающиеся прямые

Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).

Рисунок 2.14 — Скрещивающиеся прямые

2.7. Проекции плоских углов

Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.

Рисунок 2.15

По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.

Теорема о проецировании прямого угла в частном случае

Рисунок 2.16 – Проецирование прямого угла

Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,

2.8. Задачи для самостоятельного решения

1. Построить отрезок прямой АВ // π₁, равный 35 мм и наклонённый к π₂ под углом 25° (Рисунок 2.17).

Рисунок 2.17

2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π₂ и π₁.

3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π₁ и 45° — к плоскости проекций π₂.

4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π₂/π₁ (Рисунок 2.18).

Источник

Начертательная геометрия, решение задач ОмГТУ

Рабочая тетрадь для решения задач

по дисциплинe «Начертательная геометрия»

(для студентов заочной формы обучения)

Тема 1. Изображение точек на комплексном чертеже.

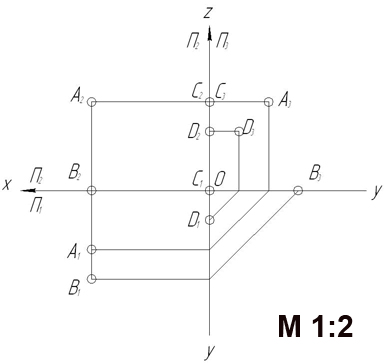
З а д а ч а 1. Построить точки А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.

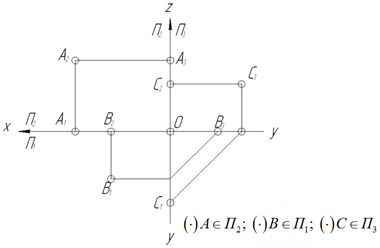
З а д а ч а 2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.

Тема 2. Прямая. Взаимное расположение прямых.

З а д а ч а 3. Даны точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить отрезки АВ и СD, обозначить и записать координаты конкурирующих точек.

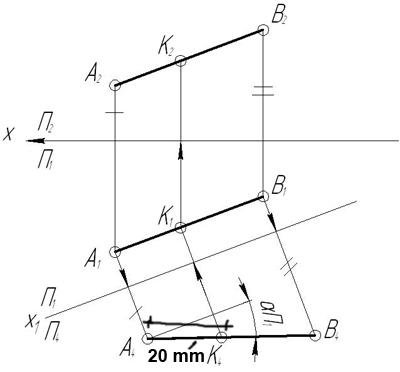
З а д а ч а 4. Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций П₁.

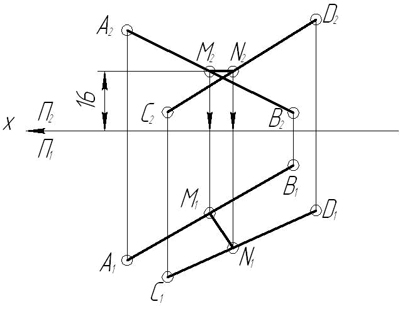
З а д а ч а 5. Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П₁ на расстоянии 16 мм.

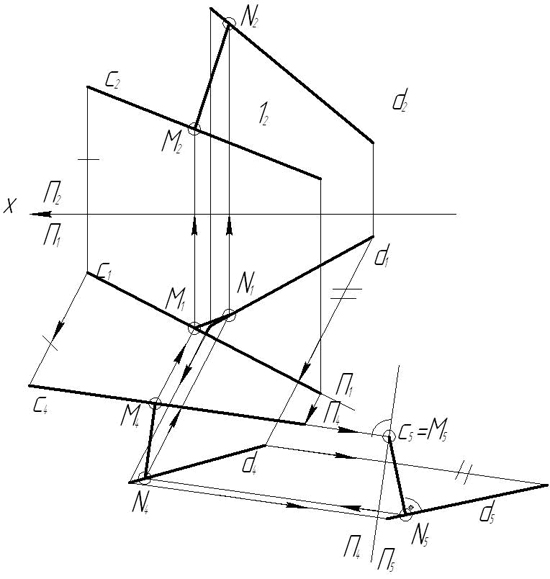
З а д а ч а 6. Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.

З а д а ч а 7. Дано: точка А(А₁,А₂) и прямая ВС общего положения. Построить сферу с центром в точке А, касательную к прямой ВС

Тема 3. Плоскость. Главные линии плоскости.

З а д а ч а 8. Дана плоскость сигма (ΔABC), точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f этой плоскости.

З а д а ч а 9. Построить недостающие проекции точек E и D, лежащих в плоскости сигма (АВ ∩ ВС).

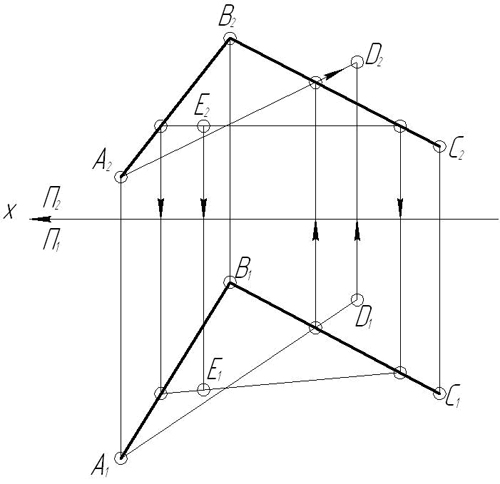
З а д а ч а 10. Дан плоский пятиугольник ABCDЕ, заданный горизонтальной и фронтальной проекциями двух смежных сторон. Достроить его фронтальную проекцию.

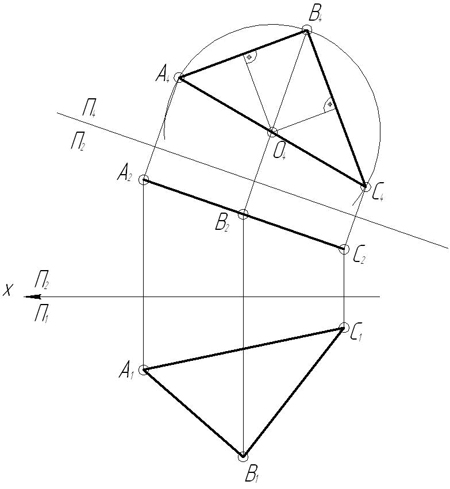
З а д а ч а 11. Дан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.

Тема 4. Взаимное расположение прямой и плоскости.

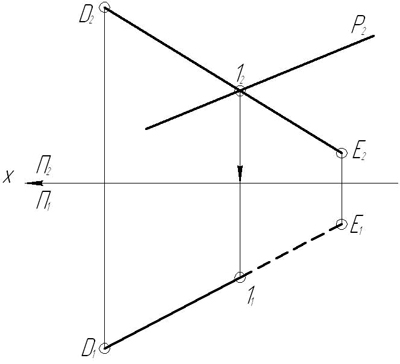
З а д а ч а 12. Задана плоскость Р и прямая DE. Найти точку пересечения прямой с плоскостью. Определить видимость проекции прямой. (Р₂ – фронтальный след плоскости). P (AB//FC).

З а д а ч а 13. Заданы плоскость Р(ΔАВС) и точка D: а) определить расстояние от точки D до плоскости Р; б) построить точку М, симметричную точке D относительно плоскости Р; в) построить шар с центром в точке D, касательный к плоскости Р.

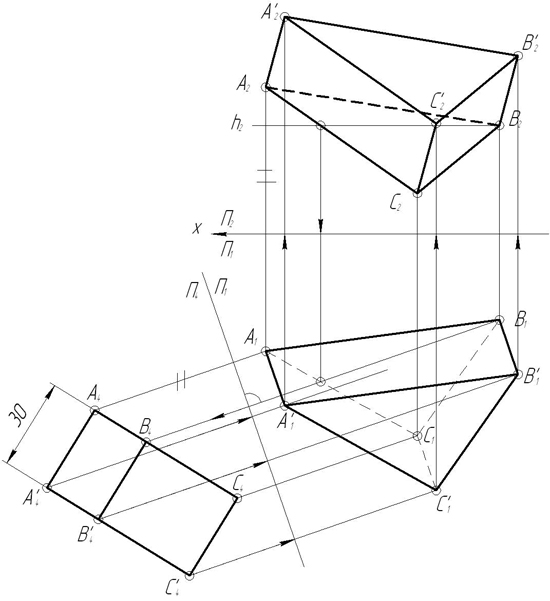
З а д а ч а 14. Задан ΔАВС общего положения. Построить прямую призму с основанием ΔАВС и высотой равной 30 мм.

Тема 5. Взаимное положение плоскостей.

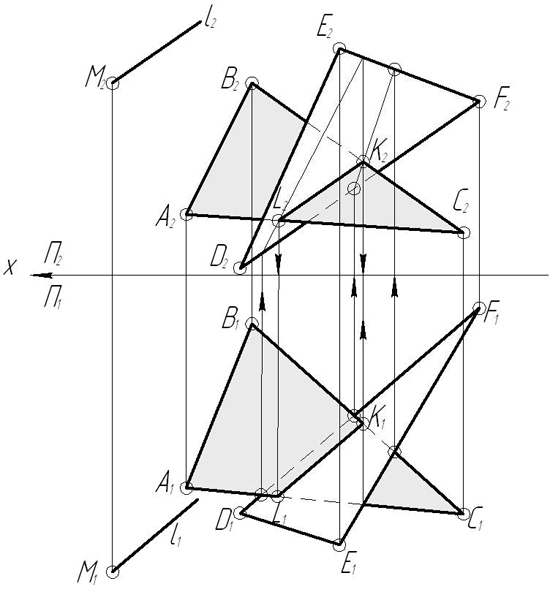
З а д а ч а 15. Даны плоскости сигма(ΔАВС), гамма(DEF) и точка М: а) построить линию пересечения плоскостей. б) через точку М провести прямую l, параллельную плоскостям сигма и гамма. Задачу решить без использования способа замены плоскостей.

З а д а ч а 16 Даны плоскость Р(а//b) и точка М. Через точку М провести плоскость Г, параллельную плоскости Р.

З а д а ч а 17 Даны плоскость Р(а//b) и прямая CD. Через прямую CD провести плоскость Г перпендикул. Р. Г(ΔСDE)

З а д а ч а 18

Тема 7. Пересечение поверхности с плоскостью

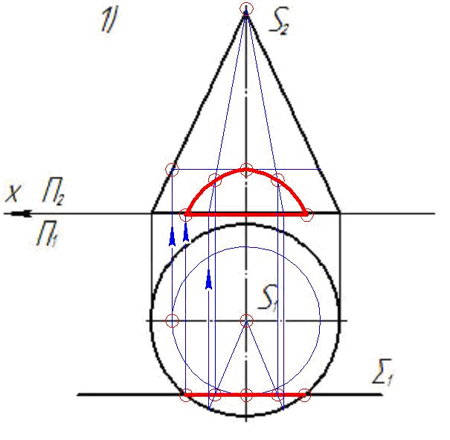
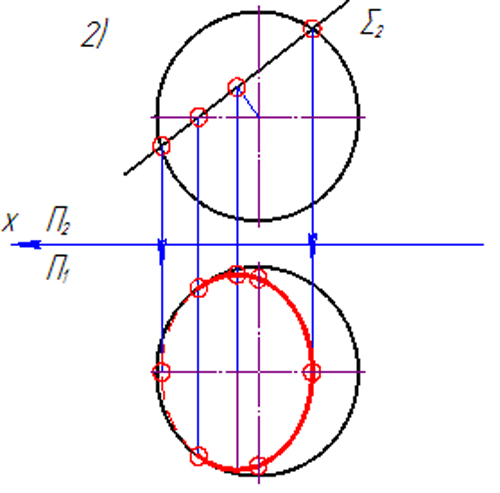
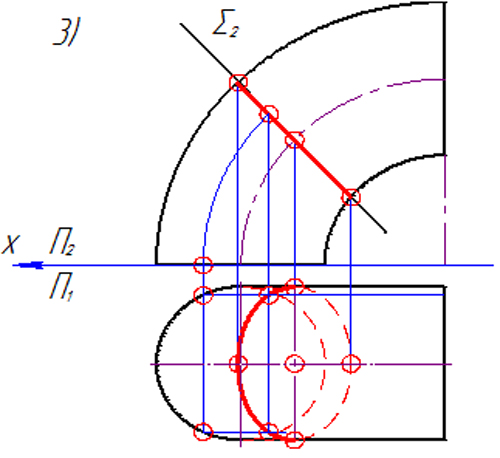
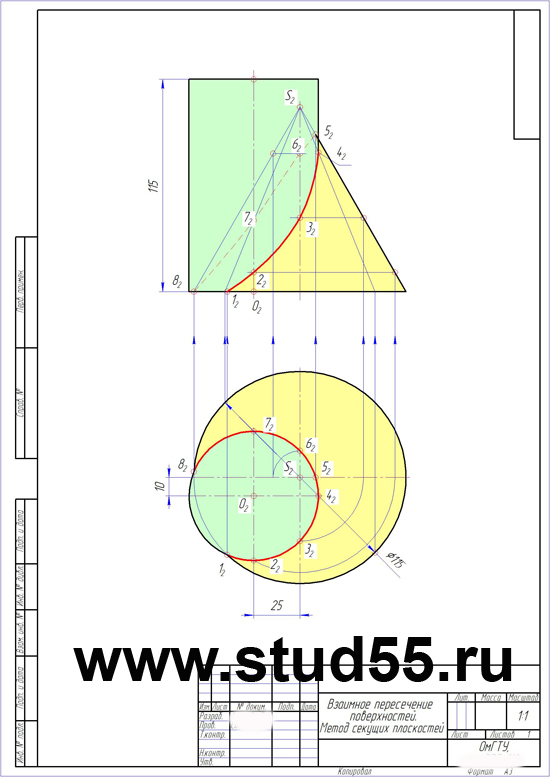
З а д а ч а 19. Построить проекции сечения данной поверхности проецирующей плоскостью Σ.

Тема 8. Пересечение прямой линии с поверхностью

З а д а ч а 20. Построить точки пересечения прямой с заданной поверхностью. Установить видимость проекций прямой

Тема 10. Взаимное пересечение поверхностей.

З а д а ч а 21 Метод вспомогательных секущих плоскостей

З а д а ч а 22 Метод сферического посредника

Источник

Примеры решения задач. 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).

1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).

Дано: Решение:

2. Разделить отрезок АВ точкой С в отношении 2:3 (рис.13).

Дано: Решение:

Для того, чтобы построить точку С, делящую отрезок в заданном отношении, достаточно одну из проекций отрезка (на рис. 13 горизонтальная проекция) разделить в этом отношении, а затем построить вторую проекцию искомой точки, используя линию связи. Деление проекции А₁В₁ произведено с помощью теоремы Фалеса. Для этого из любого конца проекции А₁В₁, например из точки А₁ проводим луч под произвольным углом, на котором откладываем 2+3=5 равных отрезков произвольной длины. Соединяем точки В₀В₁, затем проводим через С₀ прямую С₀С₁||B₀B₁.

Пример 4. Достроить отрезок АВ, если длина его равна 50 мм (рис.14).

Задача является обратной к определению истинной величины отрезка прямой.

Дано: Решение:

Для того, чтобы достроить фронтальную проекцию точки A(A₂) необходимо знать разность удалений концов отрезка АВ от плоскости p₁: Dz=z_В-z_А, значение которой можно узнать, построив прямоугольной треугольник, взяв за один из катетов известную горизонтальную проекцию отрезка АВ. Треугольник построен по известному катету и гипотенузе (известной истинной величине отрезка АВ). Из прямоугольного треугольника А₁В₁В₀ находим, что Dz=|В₁В₀|. Задача имеет два решения (две точки A₂ и A’₂).

Пример 5. На прямой a (a₁,a₂) от точки А отложить отрезок АС, длиной 30 мм (рис.15).

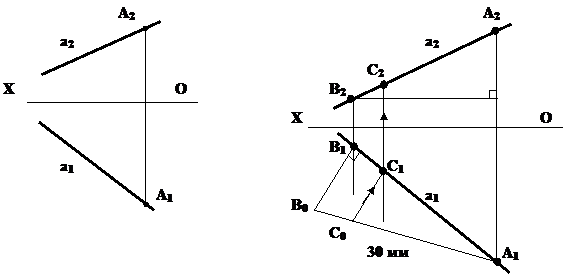На прямой а зададимся произвольным отрезком АВ. С помощью прямоугольного треугольника А₁В₁В₀ определим истинную величину отрезка АВ. Далее от точки А₁ откладываем вдоль гипотенузы заданный отрезок 30 мм. Определяем искомую точку С(С₁,С₂), используя положение о пропорциональности деления отрезка, при этом С₀С₁||В₀В₁.

Пример 6. (Задача на профильные прямые). Достроить прямую NM, параллельную прямой КL (рис.16).

Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.

Дано: Решение:

Для того, чтобы построить недостающую фронтальную проекцию N₂ точки N, воспользуемся методом вспомогательных прямых. Суть его заключается в следующем. Для исходных профильных прямых методом косоугольного проектирования строятся вспомогательные прямые. По взаимному положению вспомогательных прямых судят о взаимном положении соответствующих им профильных прямых: если вспомогательные прямые параллельны, то параллельны соответствующие профильные прямые, если вспомогательные пересекаются, то исходные прямые или пересекаются или скрещиваются. Построим вспомогательную прямую для прямой KL. Для этого из точек K₁ и K₂ проведем лучи произвольного направления до пересечения в точке K₀. Точка К₀ – является вспомогательной для точки К. Аналогично строим точку L₀ – вспомогательную для точки L. При этом [L₁L₀)|| [K₁K₀), [L₂L₀)|| [K₂K₀). Прямая К₀L₀ является вспомогательной для прямой KL. Так как точка M, принадлежащая второй профильной прямой определена однозначно (известны обе ее проекции), построим вспомогательную ей точку М₀, при построении которой должна быть соблюдена параллельность проецирующих лучей на соответствующих проекциях: [М₁М₀)|| [K₁K₀)|| [L₁L₀) и [М₂М₀)|| [K₂K₀)|| [L₂L₀). Так как исходные прямые должны быть параллельны, поэтому через построенную точку М₀ зададим направление вспомогательной прямой М₀N₀, параллельно прямой K₀L₀. Для нахождения точки L₀ проведем проецирующий луч из точки L₁, параллельно лучам на горизонтальной проекции до пересечения с прямой, проведенной из точки M₀. Точка пересечения L₀будет являться вспомогательной для точки L, с помощью которой отыскивается неизвестная фронтальная проекция L₂ точки L.

Задачи для самостоятельного решения.

Задача 1. Достроить недостающую проекцию точки С, принадлежащей отрезку АВ, а также определить истинную величину отрезка АВ и углы его на клона к плоскостям проекций (рис.17 а, б).

Задача 2. Построить на эпюре и в аксонометрии изображение прямой, проходящей через точки А(50,40,10) и В(25,10,30). Определить истинную величину отрезка АВ.

Задача 3. Определить относительное положение прямой а и точек А, В, С и D (рис.18).

Задача 4. Построить проекции точек А, В и С, принадлежащих прямой а, если z_A=15, z_B=y_A, z_C=y_C.(рис.19).

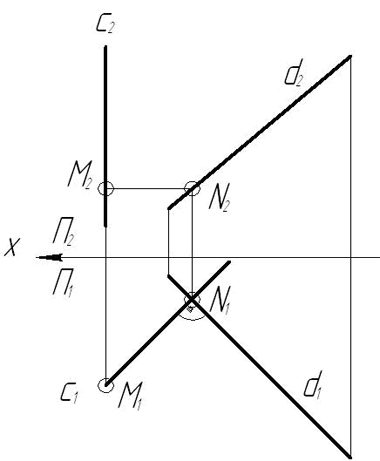
Задача 5. Определить взаимное положение прямых а и b (рис.20).

Задача 6. Задана прямая m||p₂. На расстоянии 30 мм от m построить прямую n||m. (При решении использовать теорему о проецировании прямого угла)(рис.21).

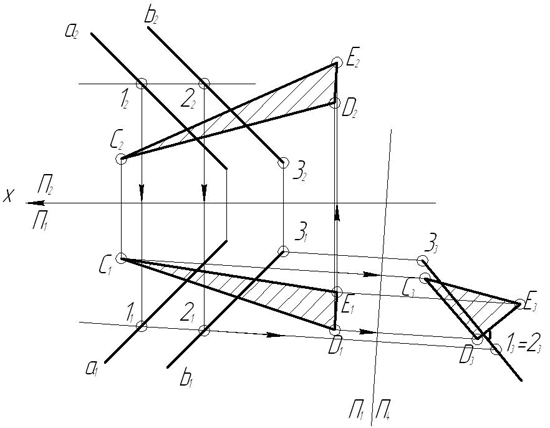
Задача 7. Пересечь прямые a и b прямой, параллельной p₂ и отстоящей от фронтальной плоскости проекций на 20 мм (рис.22).

Задача 8. Построить проекции прямой, проходящей через точку С и пересекающей прямые а и b. Определить положение прямой b относительно плоскостей проекций (рис.23). Для прямой b определить видимость точек, ограничивающих отрезок этой прямой.

Задача 9. Через точку С провести прямую DE, пересекающую прямую а и перпендикулярную ей (а||p₂) (рис.24).

Задача 10. Через точку С провести прямую, параллельную отрезку АВ (рис.25).

Задача 11.Построить прямую, отсекающую на отрезках CD и EF участки CK и EF участки СK и EN, длиной 35 мм каждый (рис.26).

Задача 12. Достроить проекции треугольника АВС, если истинная величина сторон АВ=60 мм, ВС=50 мм. Определить угол наклона стороны АС к плоскости p₁ (рис.27).

Задача 13. Определить расстояние от точки С до прямой m (m₁, m₂)(рис.28).

Задача 14. Достроить равнобедренный треугольник АВС с основанием ВС (рис.29).

Пример 15. Через точку К, принадлежащую отрезку АВ, провести прямую КL, пересекающую отрезок АВ, параллельную плоскости p₁ и наклоненную к p₂ под углом 45 0 (рис.30).

3. ПЛОСКОСТЬ. ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ.

ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ.

ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ.

3.1.Основные теоретические положения.

Плоскость в пространстве однозначно определена тремя точками, не лежащими на одной прямой. В связи с этим существует несколько способов задания плоскости на эпюре, среди которых отметим следующие (рис.31):

1) тремя точками, не принадлежащими одной прямой (рис.31,а);

2) любой плоской фигурой, например, треугольником (рис.31,б);

3) прямой, и не принадлежащей ей точкой (рис.31,в);

4)

двумя пересекающимися прямыми (рис.31,г);

5) двумя параллельными прямыми (рис.31,д).

Виды плоскостей. Плоскость, произвольно расположенная в пространстве (по отношению к плоскостям проекций), называется плоскостью общего положения. Все плоскости, изображенные на рис.31 являются плоскостями общего положения.

Плоскость, перпендикулярная одной или двум плоскостям проекций, называется плоскостью частного положения, причем плоскость перпендикулярная одной из плоскостей проекций носит название проецирующей плоскости: горизонтально проецирующей если a^p₁ или фронтально-проецирующей a^p₂ (рис.32). На эпюрах проецирующие плоскости задаются своим следом на соответствующей плоскости проекций.

Рис.32.

Прямая принадлежит плоскости, если:

а) имеет, по крайней мере, две общие с плоскостью точки (прямая b, рис.33) ;

б) когда она имеет одну общую точку и параллельна какой-либо прямой в этой плоскости (прямая aêê(BC), рис.33).

Через любую точку плоскости можно провести главные линии плоскости – фронталь и горизонталь, прямые, лежащие в плоскости и параллельные либо p₁ либо p₂ соответственно. Таких линий в плоскости можно провести сколько угодно.

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости.

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой. Если параллельны две проецирующие плоскости, то на эпюре параллельны из одноименные следы.

Две плоскости пересекаются по прямой линии. Для построения линии пересечения двух плоскостей достаточно построить две точки, принадлежащей одновременно двум заданным плоскостям. Для построения линии пересечения двух плоскостей общего положения обычно используют метод вспомогательных секущих плоскостей.

Пример1. Достроить плоский четырехугольник (рис.34).

Дано: Решение:

Решение задачи сводится к построению недостающей проекции точки D, принадлежащей плоскости, заданной точками А,В,C. Зададим эту плоскость треугольником АВC, для чего соединим точки В и C прямой линией на обеих проекциях. Проведем фронтальную проекцию диагонали четырехугольника А₂D₂. Затем достроим вторую ее проекцию, для чего из точки пересечения фронтальных проекций диагоналей (точка О₂) опустим линию проекционной связи на прямую D₁C₁. Прямая А₁О₁ задаст направление диагонали четырехугольника на горизонтальной проекции. Пересекаем Прямую А₁О₁ с соответствующей линией связи (из D₂), получаем искомую проекцию точки С. Точка С принадлежит плоскости треугольника АВС, т.к. принадлежит прямой АО, лежащей в этой плоскости. Прямая принадлежит плоскости треугольника АВС, т.к. имеет с ней две общие точки (А и О). Следовательно, достроенный четырехугольник – плоский.

Пример 2. Достроить точку А, если она принадлежит плоскости D ВСD (рис.35).

Пример 3. Через заданную точку Е с помощью главных линий построить плоскость b(hÇf) параллельно заданной плоскости a(a||b). Построенную плоскость задать параллельными прямыми (рис.36).

Дано:

Пример 4. Построить линию пересечения двух плоскостей: плоскости общего положения a(aÇb) и фронтально-проецирующей плоскости b(b₂)(рис.37).

Дано: Решение:

Пример 5. Построить линию пересечения двух плоскостей общего положения: a(DАВС) и b(а||b)(рис.38).

Дано:

При решении этой задачи используется метод секущих плоскостей. Так как две плоскости пересекаются по прямой линии, определяемой двумя точками, для построения необходимо ввести две дополнительные секущие плоскости. Порядок решения задачи:

1. Вводим дополнительную секущую плоскость d( d₂). В качестве секущей плоскости выбрана фронтально-проецирующая плоскость, заданная своим следом на фронтальной плоскости проекций. (В качестве секущей плоскости может быть выбрана произвольная проецирующая плоскость).

2. Строим линию пересечения фронтально-проецирующей плоскости d(d₂) с плоскостью общего положения a(DАВС) (см.пример 4): 12(1₁2₁;1₂2₁)= d( d₂) Ça(DАВС).

3. Строим линию пересечения фронтально-проецирующей плоскости d(d₂) с плоскостью общего положения b(а||b): 34(3₁4₁;3₂4₂)= d( d₂) Çb(а||b).

5. Аналогично строится вторая точка, принадлежащая линии пересечения N. Для этого вводится еще одна вспомогательная секущая плоскость g(g₂). Плоскость g(g₂) также является фронтально-проецирующей плоскостью, кроме того, параллельной плоскости d( d₂). Это является необязательным, поскольку вспомогательные плоскости могут быть выбраны совершенно произвольно.

6. После построения точки N проводим прямую MN, которая является искомой линией пересечения двух исходных плоскостей.

Пример 6. Построить линию пересечения двух плоскостей общего положения a(DАВС) и b(DDEF) (рис.39).

Решение:

Задача решается аналогично предыдущей. Для уменьшения количества вспомогательных построений в качестве секущих введены плоскости d( d₂) и g(g₂) через прямые, принадлежащие одной из плоскостей (DE и DF), следы секущий плоскостей совпадают соответствующими проекциями этих прямых.

Источник